【刷题笔记】笔记三
凑算式(蓝桥真题)
题目:

注意:需要通分,有些时候除不尽需要通分。
源码:
方法一:递归回溯全排列
int ret = 0;
#define MAX 9
//多少个全排列
int a[MAX];//排列数组
bool flag[MAX];//标记数组
int n = MAX;
//全排列n个数
void Init()
{//初始化标记为
for (int i = 0; i < MAX; i++)
{
flag[i] = true;
}
}
bool check()
{
int x = a[3] * 100 + a[4] * 10 + a[5];
int y = a[6] * 100 + a[7] * 10 + a[8];
if (((a[1] * y + a[2] * x) % (a[2] * y) == 0) && a[0] + (a[1] * y + a[2] * x) / (a[2] * y) == 10){
return true;
}
return false;
}
void dfs(int storey)
{
if (storey == MAX)//如果深度达到MAX就返回{
//检查
if (check())
ret++;
return;
}
for (int i = 0; i < MAX; i++){
if (flag[i] == true){//判断此位置是否被使用
flag[i] = false;//此数字被使用。
a[storey] = i+1;//给该层赋值
dfs( storey+ 1);//执行下一层
flag[i] = true;//回溯//让此数字没有被使用。
}
}
}
int main(){
Init();
dfs(0);//递归深度从0开始
cout << ret;
return 0;
}方法二:next_permutation全排列
#include<iostream>
#include<algorithm>
using namespace std;
#define SIZE 9
int a[SIZE] = { 1,2,3,4,5,6,7,8,9};
int ret = 0;
bool check()
{
int x = a[3] * 100 + a[4] * 10 + a[5];
int y = a[6] * 100 + a[7] * 10 + a[8];
//(a[1] * y + a[2] * x) % (y * a[2]) == 0 && a[0] + (a[1] * y + a[2] * x) / (y * a[2]) == 10
if (((a[1] * y + a[2] * x) % ( y*a[2] ) == 0) && a[0] + (a[1] * y + a[2] * x) / (y*a[2]) == 10){
return true;
}
return false;
}
void test1(){
do {
if (check() == true){
ret++;
}
} while (next_permutation(a, a + 9));
}
int main()
{
test1();
cout << ret;
return 0;
}知识点:
1.next_permutation生成全排列得使用
2.理解递归回溯生成全排列
三羊献瑞(蓝桥真题)
题目描述:
祥 瑞 生 辉 a b c d
+ 三 羊 献 瑞 e f g b
--------------------------------------
三 羊 生 瑞 气 e f c b h还是可以看成全排列的问题。
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
int a[10] = { 0,1,2,3,4,5,6,7,8,9 };
bool check()
{
int add1 = a[0] * 1000 + a[1] * 100 + a[2] * 10 + a[3];
int add2 = a[4] * 1000 + a[5] * 100 + a[6] * 10 + a[1];
int sum = a[4] * 10000 + a[5] * 1000 + a[2] * 100 + a[1] * 10 + a[7];
if (add1 + add2 == sum && a[0] != 0 && a[4]!= 0)
{
cout << add2 << endl;
return true;
}
return false;
}
int main()
{
do {
check();
} while (next_permutation(a, a + 10));
return 0;
}知识点:
next_permutation,全排列。
方格分割(蓝桥真题)
题目描述:
6x6的方格,沿着格子的边线剪开成两部分。要求这两部分的形状完全相同。
如图:就是可行的分割法。
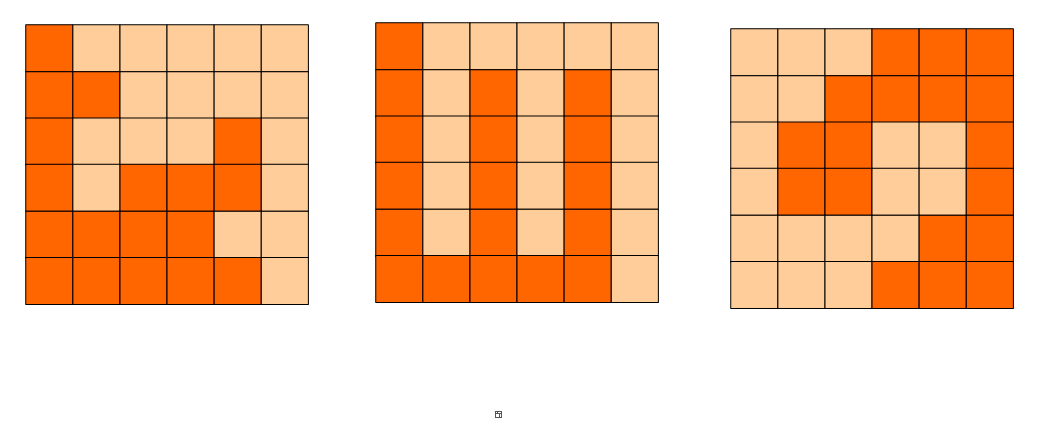
试计算:包括这3种分法在内,一共有多少种不同的分割方法。注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
说明:
如果把样例图案剪开,发现有且只有两个点在边界上,且一定经过 (3,3)点。
以(3,3)为起点进行深搜,深搜到一个边界上的点,那么他的中心对称点相当于也搜过了。
如果发现搜到了边界,那么它的中心对称点也到了边界 沿着已经搜过的点剪开,那么剪开的两个图形为中心对称图形。(要注意最终的结果要除以4)
例如 我们从(3,3)点出发一直向右到边界 , 或一直向左,或一直向上,或一直向下剪出来的图形是同一个。
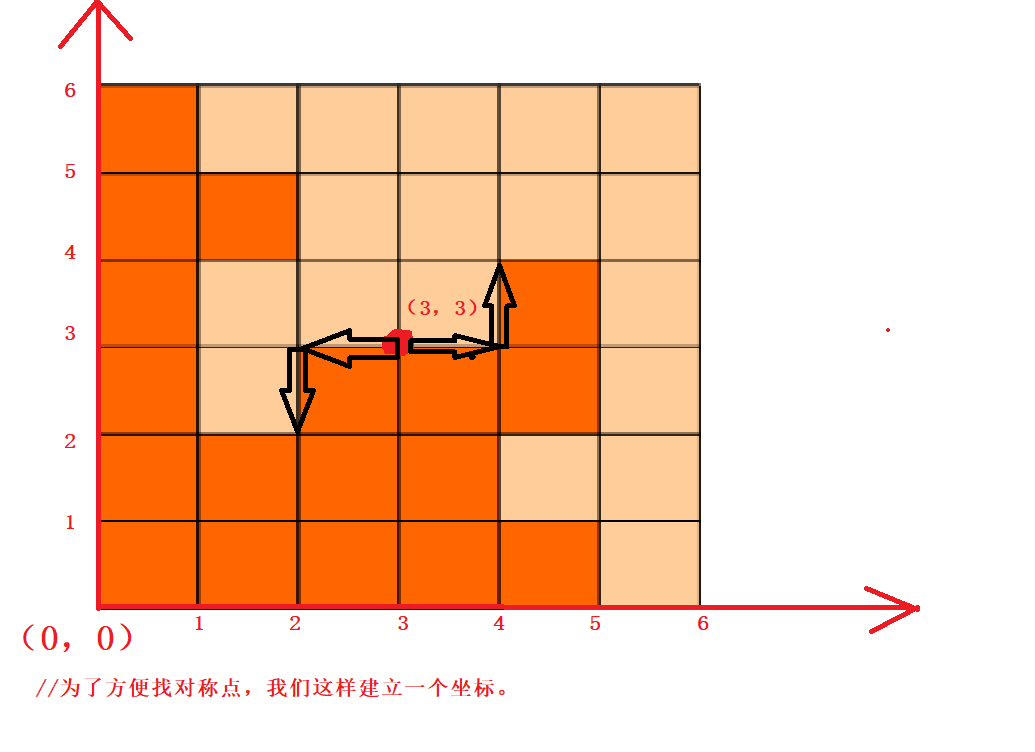
代码实现
#include<iostream>
#include<algorithm>
using namespace std;
bool vis[7][7];//标记数组
void init()
{
//初始化标记数组
for (int i = 0; i < 7; i++)
{
for (int j = 0; j < 7; j++)
{
vis[i][j] = true;
}
}
}
int ret = 0;
void dfs(int x, int y)
{
//走到边线
if (x == 0 || x == 6 || y == 0 || y == 6)
{
ret++;
return;
}
for (int i = 0; i < 4; ++i)
{
//四个方向
//(x+1,y)(x-1,y)(x,y+1)(x,y-1)
int nx;
int ny;
if (i == 0){
nx = x + 1;
ny = y;
}
if (i == 1){
nx = x - 1;
ny = y;
}
if (i == 2){
nx = x;
ny = y + 1;
}
if (i == 3){
nx = x;
ny = y - 1;
}
if (vis[nx][ny]){
vis[nx][ny] = false; vis[6 - nx][6 - ny] = false;
dfs(nx, ny);
vis[nx][ny] = true; vis[6 - nx][6 - ny] = true;
}
}
}
int main()
{
init();
vis[3][3] = false;
dfs(3, 3);
cout << ret/4 << endl;//509
return 0;
}知识点:
dfs的深度优先遍历。
方格填数(蓝桥真题)
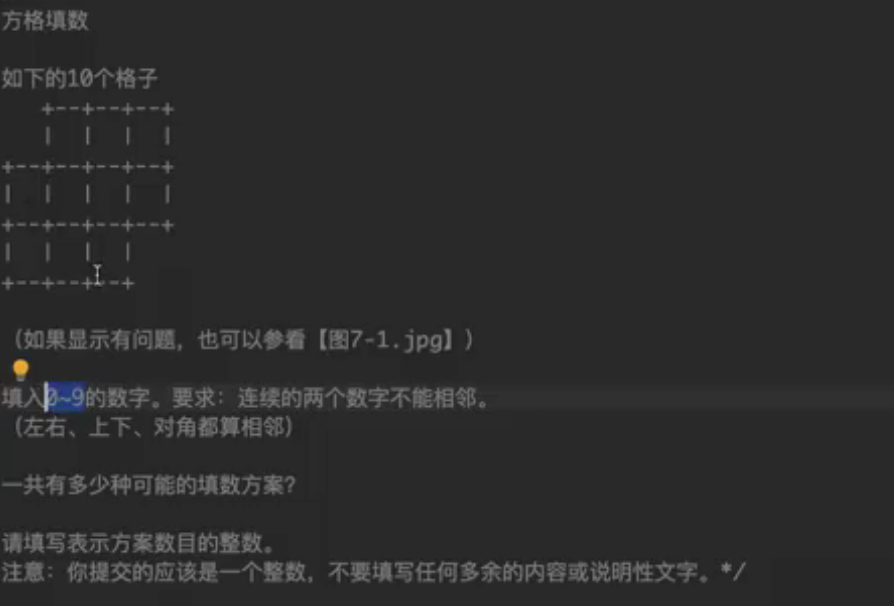
显然全排列也能搞定。
对每一种排列数进行判断。
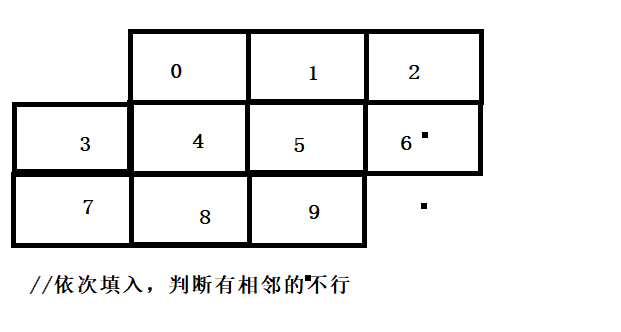
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
int a[10] = { 0,1,2,3,4,5,6,7,8,9 };
int ret = 0;
int dis(int x, int y)
{
if (a[x] - a[y] == 1 || a[x] - a[y] == -1)
{
return 1;
}
return 0;
}
bool check()
{
if (dis(0, 1) ==1||
dis(0, 3) ==1||
dis(0, 4) ==1||
dis(0, 5) ==1||
dis(1, 4) ==1||
dis(1, 5) ==1||
dis(1, 6) ==1||
dis(1, 2) ==1||
dis(2, 5) ==1||
dis(2, 6) ==1||
dis(3, 4) ==1||
dis(3, 7) ==1||
dis(3, 8) ==1||
dis(4, 5) ==1||
dis(4, 7) ==1||
dis(4, 8) ==1||
dis(4, 9) ==1||
dis(5, 6) ==1||
dis(5, 8) ==1||
dis(5, 9) == 1 ||
dis(6, 9) ==1||
dis(7, 8) ==1||
dis(9, 8)==1)
{
return false;
}
return true;
}
int main()
{
do {
if (check())
{
ret++;
}
} while (next_permutation(a, a + 10));
cout << ret << endl;//1580
return 0;
}以上是最简单的一种方式,也可以深度递归去一个一个填写,这样代码会不好理解
知识点:
只要还是用全排列,全部填入,然后判断每一个排列即可。
加法变乘法(蓝桥真题)
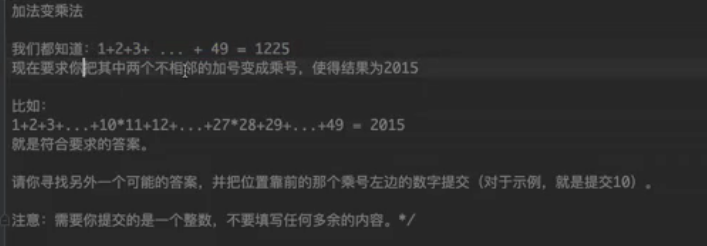
其实这个题就说遍历,遍历两个*的位置,
加号变为乘号,前后sum的变化就是加上两者相乘的情况,然后再进去两者本身就可以了。
#include<iostream>
using namespace std;
int main()
{
for (int i = 1; i < 50; i++)
{
for (int j = i + 1 ; j < 50; j++)
{
int sum = 1225 - i - i - 1 + i * (i + 1) - j - j - 1 + j * (j + 1);
if (sum == 2015)
{
cout << i <<" " << j << endl;
}
}
}
return 0;
}很简单但是稍微带一点点小技巧。
最大公共子串(蓝桥真题)
题目描述:
给定两个字符串,求出最大公共子串的长度:
分析:
这里要用到一个二位数组。且这个二维数组比两个串行列大一。

代码实现:
#include<iostream>
#include<string>
using namespace std;
int fun(const char* str1, const char* str2)
{
int max = 0;//记录最大值
int len1 = strlen(str1);
int len2 = strlen(str2);
int a[256][256];
memset(a, 0, sizeof(int) * 256 * 256);//首先全部初始化位0;
for (int i = 0; i < len1; i++)
{
for (int j = 0; j < len2; j++)
{
if (str1[i] == str2[j])
{
a[i + 1][j + 1] = a[i][j] + 1;
if (a[i + 1][j + 1] > max)
{
max = a[i + 1][j + 1];
}
}
}
}
return max;
}
int main()
{
cout << fun("zhangzxnsk", "axsk") << endl;
return 0;
}最大黑区域的问题(DFS)
题目描述:
{0,1,1,0,0,1},
{1,1,0,1,0,1},
{0,1,0,0,1,0},
{0,0,0,1,1,1},
{1,0,1,1,1,0},
//假设1是黑块,0是白块,求出黑色的块最大联通块的面积。
//每个块面积是1,
//只有上下左右相邻的才算是联通。斜着链接不是联通。源码:
//坐标移动的四个方向
int ll[4][2] = {
{1,0},
{-1,0},
{0,1},
{0,-1}
};
//原始的二维数组。
int arr[5][6] = {
{0,1,1,0,0,1},
{1,1,0,1,0,1},
{0,1,0,0,1,0},
{0,0,0,1,1,1},
{1,0,1,1,1,0}
};
int _max = 0;//当前最大面积
int s = 0;//面积
void dfs(int x, int y)
{
s += 1;//面积+1
arr[x][y] = 0;//记录这里统计过。
for (int i = 0; i < 4; i++)
{
int nx = x + ll[i][0];
int ny = y + ll[i][1];
if (ny>=0 && ny>=0 && nx <= 4&& ny <= 5 && arr[nx][ny] == 1) dfs(nx, ny);
}
}
int main()
{
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 6; j++)
{
//先找到一个黑区域
if (arr[i][j] == 1)
{
//从i,j 开始dfs。
s = 0;//注意每次dfs时候都要先把面积变为0
dfs(i, j);
if (s >_max)
{
_max = s;
}
}
}
}
cout << _max << endl;
return 0;
}剪邮票(蓝桥真题)
#include<iostream>
#include<algorithm>
using namespace std;
int a[12] = { 0,0,0,0,0,0,0,1,1,1,1,1 };
int ll[4][2] = {
{1,0},
{-1,0},
{0,1},
{0,-1}
};
int flag[3][4] = { 0 };
int m = 0;//记录每一次查找的最大联通数
void dfs(int x, int y)
{
flag[x][y] = 0;//表示已经统计过
m++;
if (m == 5) return;
for (int i = 0; i < 4; i++)
{
int nx = x + ll[i][0];
int ny = y + ll[i][1];
if (nx >= 0 && ny >= 0 && nx < 3 && ny < 4 && flag[nx][ny] == 1) {
dfs(nx, ny);
//此题不需要回溯
}
}
}
bool check()
{
//在数组中填写标记位。
int size = 0;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 4; j++)
{
flag[i][j] = a[size++];
}
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 4; j++)
{
if (flag[i][j] == 1)//找到其中一个标记位置
{
m = 0;
dfs(i, j);
if (m == 5)
{
return true;
}
}
}
}
return false;
}
int ret = 0;
int main()
{
do {
if (check())
{
ret++;
}
} while (next_permutation(a, a + 12));
cout << ret << endl;
return 0;
}日期问题(蓝桥真题)
题目描述:

讲解:
题目不难但是很考验细心程度,需要控制各种各样的不成立问题,
例如:考虑二月的问题,闰年,大小月份的问题。最后还要去重和排序。
实现代码:
#include<iostream>
#include<string>
#include<set>
using namespace std;
int day[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
bool isleap(int year)
{
return (year % 4 == 0 && year % 100 != 0) || (year % 400 == 0);
}
string check(int a, int b, int c)//a是年,b是月,c是日
{
//处理年
if (a >= 60 && a < 99) { a += 1900; }
else if (a >= 0 && a < 59) { a += 2000; }
else { return ""; }
//处理月
if (b < 0 || b>12)return "";
//处理日
if (isleap(a)) { day[2] = 28; }
if (day[b] < c) { return "";}
string _year = to_string(a);
string _monch = to_string(b);
if (b < 10) { _monch.insert(0, 1, '0'); }
string _day = to_string(c);
if (c < 10) { _day.insert(0, 1, '0'); }
string ret = _year +"-"+ _monch + "-" + _day;
return ret;
}
int main()
{
string strin;
cin >> strin;
//按顺序记录三个数字。
int a = (strin[0] - '0') * 10 + (strin[1] - '0');
int b = (strin[3] - '0') * 10 + (strin[4] - '0');
int c = (strin[6] - '0') * 10 + (strin[7] - '0');
string str1 = check(a, b, c);
string str2 = check(c, a, b);
string str3 = check(c, b, a);
set<string> ret;
if (str1 != "") ret.insert(str1);
if (str2 != "") ret.insert(str2);
if (str3 != "") ret.insert(str3);
for (auto e : ret)
{
cout << e << endl;
}
return 0;
}买不到的数目(蓝桥真题)
题目描述:

分析:
1.这是一个不定方程的问题。
2.“a*x+b*y = c“有解问题。
3.根据数学原理:
a和b互质,一定存在最大凑不出的数是:“a*b-a-b”。
a和b不互质,即gcd(a,b)>1时,任意的an+bm-1都无法实现,有无限个凑不出的数。
实现代码:
#include<iostream>
using namespace std;
int main()
{
int n1, n2;
while (cin >> n1 >> n2)
{
cout << n1 * n2 - n1 - n2 << endl;
}
return 0;
}包子凑数(蓝桥真题)
题目描述:

分析:
1.这是一个不定方程的问题。
2.“a1*x1+a2*x2 ---- an*xn = c“ 有解问题。
3.根据数学原理:
a1,a2,a3---an互质,一定存在最大凑不出的数是:“a*b-a-b”。
a1,a2,a3---an不互质,即gcd(a,b)>1时,任意的an+bm-1都无法实现,有无限个凑不出的数。
4.首先根据n<100 & ai<100,可以得到无法组成的最大数就是10000。也可以根据 a,b无法组成的最大数为a*b-a-b确定是 9800。
5.先求出一组数的最小公倍数,当cgcd!=1时,答案就为INF,因为a*n+b*m-1总是无法组成
6.定义一个maxnumm == 10000长度的数组。
7.遍历1~maxnum,动态规划标记所有能访问的点,未标记的个数就是ans;
实现代码:
#include<iostream>
using namespace std;
int n = 0;//种类数
int arr[100];//存放包子数
bool flag[10000];
//下标对应的数字,可凑出来标记为true,凑不出来标记为false
//互质是:公约数只有1的两个整数是互质
//最大公约数
int gcd(int a, int b)
{
if (b == 0)return a;
else return gcd(b, a % b);
}
int g = 0;
int ret = 0;
int main()
{
flag[0] = true;//0肯定是能凑出来的。
for (int i = 1; i < 10000; i++)
{
flag[i] = false;
}
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> arr[i];//从小到大输入
}
//数据输入完成
for (int i = 0; i < n ; i++)
{
if (i == 0) { g = arr[i]; }
else { g = gcd(arr[i], g); }
for (int j = 0; j < 9900; j++)
{
if (flag[j] == true) { flag[j + arr[i]] = true; }
}
}
if (g != 1) {
cout << "INF" << endl;
return 0;
}
for (int j = 0; j < 9900; j++)
{
if (!flag[j]) { ret++; cout << j << endl;}
}
cout << ret << endl;
return 0;
}
