当前位置： 首页 > article >正文

【二叉树OJ题(二)】前序遍历中序遍历后序遍历另一颗树的子树二叉树遍历平衡二叉树

article 2024/11/16 17:57:45

​在这里插入图片描述

​📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：数据结构
🎯长路漫漫浩浩，万事皆有期待

文章目录

  • 二叉树OJ练习(二)
    • 1、二叉树的前序遍历
    • 2、二叉树的中序遍历
    • 3、二叉树的后序遍历
    • 4、另一颗树的子树
    • 5、二叉树遍历
    • 6、平衡二叉树
  • 总结：

上一篇博客：【二叉树OJ题(一)】

二叉树OJ练习(二)

1、二叉树的前序遍历

链接：144. 二叉树的前序遍历
题述：给你二叉树的根节点 root ，返回它节点值的前序遍历。
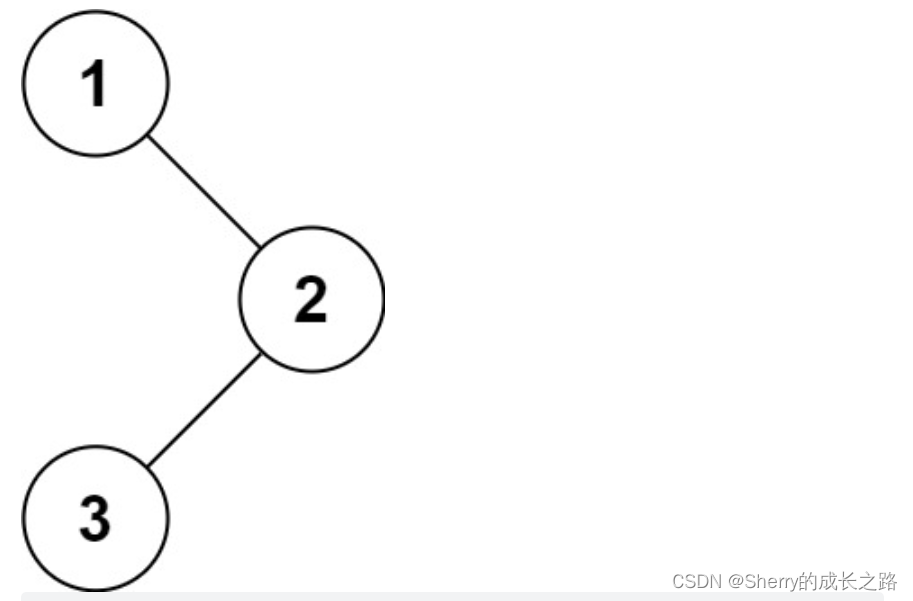
在这里插入图片描述

示例 1：
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]
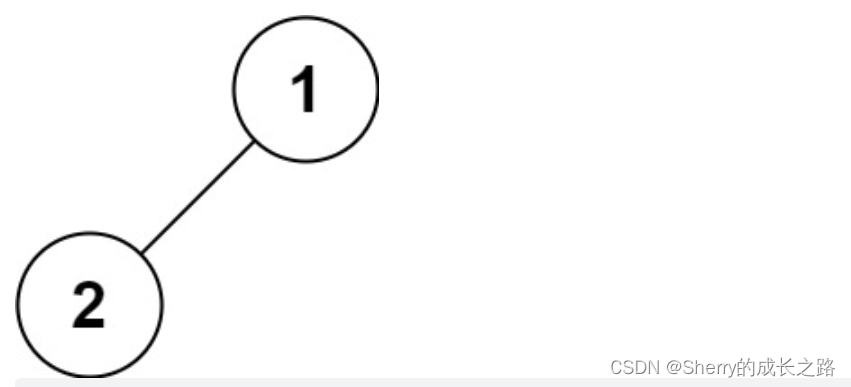
在这里插入图片描述

示例 4：
输入：root = [1,2]
输出：[1,2]
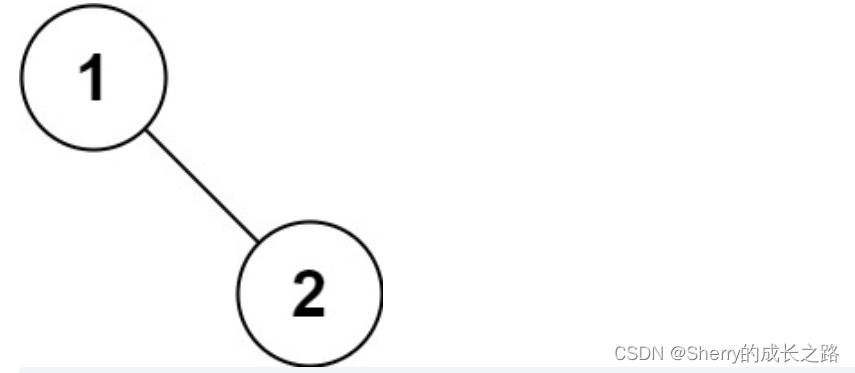
在这里插入图片描述

示例 5：
输入：root = [1,null,2]
输出：[1,2]

注意：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

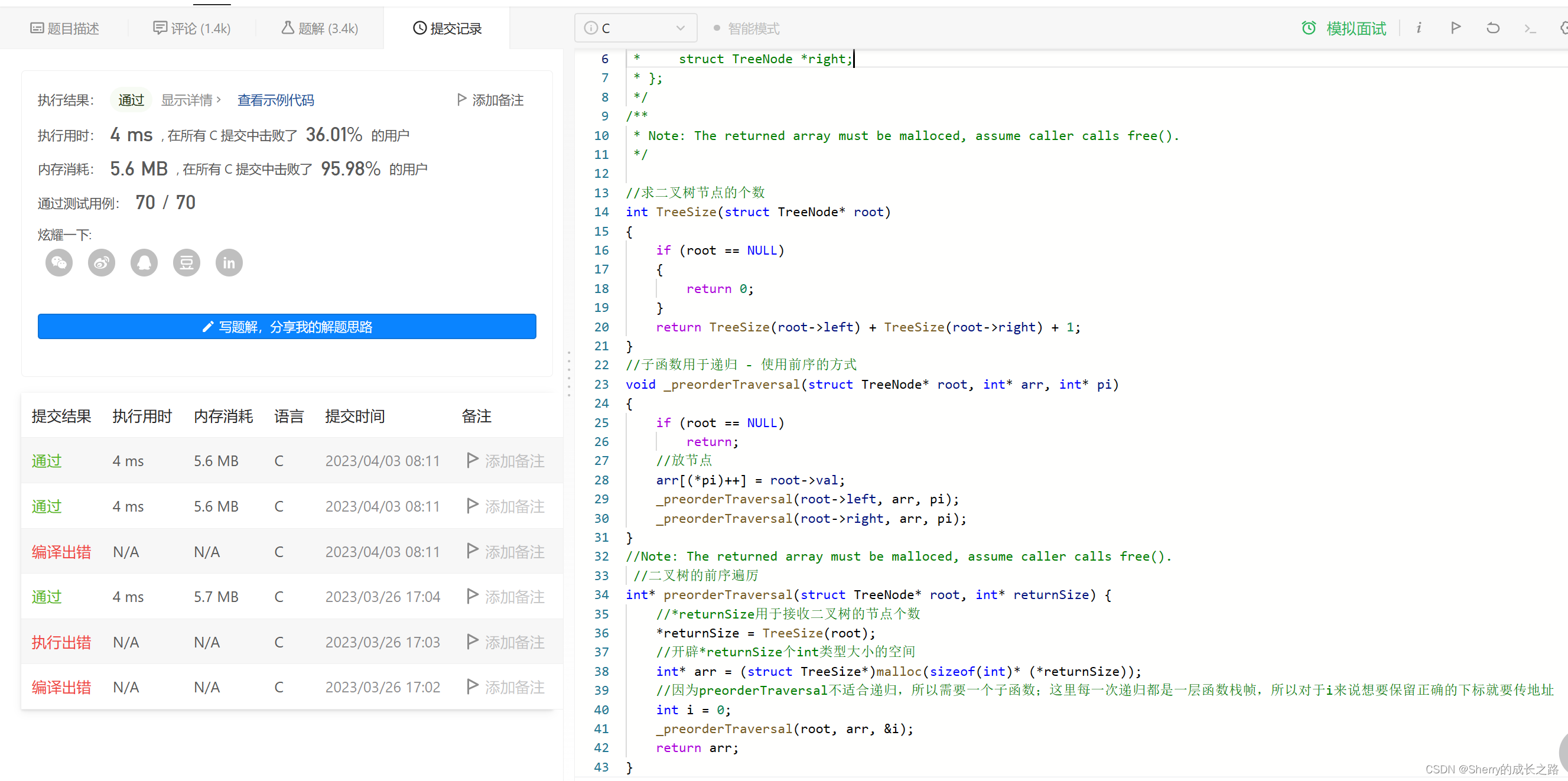
注意:这里的题目，要求我们将遍历结果存到数组中，将数组返回，且空指针不需要记录。那么我们可以计算出二叉树的大小，然后 动态开辟一个二叉树大小的数组。
并使用一个下标来记录数组的元素个数，最后 前序遍历二叉树 ，将结果存入数组，返回数组。

核心思想：可以先实现 TreeSize 函数 计算出二叉树的节点个数给 returnSize，并开辟好 returnSize 个 int 类型大小的数组。再调用子函数进行前序递归：如果每层函数栈帧中节点为空则结束栈帧，否则把节点放到数组里，并继续递归

//求二叉树节点的个数
int TreeSize(struct TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//子函数用于递归 - 使用前序的方式
void _preorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
	if (root == NULL)
		return;
	//放节点
	arr[(*pi)++] = root->val;
	_preorderTraversal(root->left, arr, pi);
	_preorderTraversal(root->right, arr, pi);
}
//Note: The returned array must be malloced, assume caller calls free().
 //二叉树的前序遍厉
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
	//*returnSize用于接收二叉树的节点个数
	*returnSize = TreeSize(root);
	//开辟*returnSize个int类型大小的空间
	int* arr = (struct TreeSize*)malloc(sizeof(int)*(*returnSize));
	//因为preorderTraversal不适合递归，所以需要一个子函数；这里每一次递归都是一层函数栈帧，所以对于i来说想要保留正确的下标就要传地址
	int i = 0;
	_preorderTraversal(root, arr, &i);
	return arr;
}

在这里插入图片描述

2、二叉树的中序遍历

94. 二叉树的中序遍历
题述：给定一个二叉树的根节点 root ，返回它的中序遍历。
在这里插入图片描述

示例 1：
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

示例 4：
输入：root = [1,2]
输出：[1,2]

示例 5：
输入：root = [1,null,2]
输出：[1,2]

注意：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

核心思想：类似前序

//求二叉树节点的个数
int TreeSize(struct TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//子函数用于递归 - 使用中序的方式
void _inorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
    if(root == NULL)
        return;
    _inorderTraversal(root->left, arr, pi);
    arr[(*pi)++] = root->val;
    _inorderTraversal(root->right, arr, pi);
}
//Note: The returned array must be malloced, assume caller calls free().
//二叉树的中序遍厉
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    //*returnSize接收二叉树的节点个数
    *returnSize = TreeSize(root);
    //开辟*returnSize个int类型大小的空间
    int* arr = (struct TreeNode*)malloc(sizeof(int)* * returnSize);
    //递归调用子函数
    int i = 0;
    _inorderTraversal(root, arr, &i);
    return arr;
}

在这里插入图片描述

3、二叉树的后序遍历

145. 二叉树的后序遍历
题述：给定一个二叉树，返回它的后序遍历。
在这里插入图片描述

示例 1：
输入: [1,null,2,3]
输出: [3,2,1]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

核心思想：类似前序

//求二叉树节点的个数
int TreeSize(struct TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//子函数用于递归 - 使用后序的方式
void _postorderTraversal(struct TreeNode* root, int* arr, int* pi)
{
	if (root == NULL)
		return;
	_postorderTraversal(root->left, arr, pi);
	_postorderTraversal(root->right, arr, pi);
	arr[(*pi)++] = root->val;
}
//Note: The returned array must be malloced, assume caller calls free().
//二叉树的后序遍历
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
	//*returnSize接收二叉树的节点个数
	*returnSize = TreeSize(root);
	//开辟*returnSize个int类型大小的空间
	int* arr = (struct TreeNode*)malloc(sizeof(int)* * returnSize);
	//递归调用子函数
	int i = 0;
	_postorderTraversal(root, arr, &i);
	return arr;
}

在这里插入图片描述

4、另一颗树的子树

链接：572. 另一棵树的子树
题述：给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
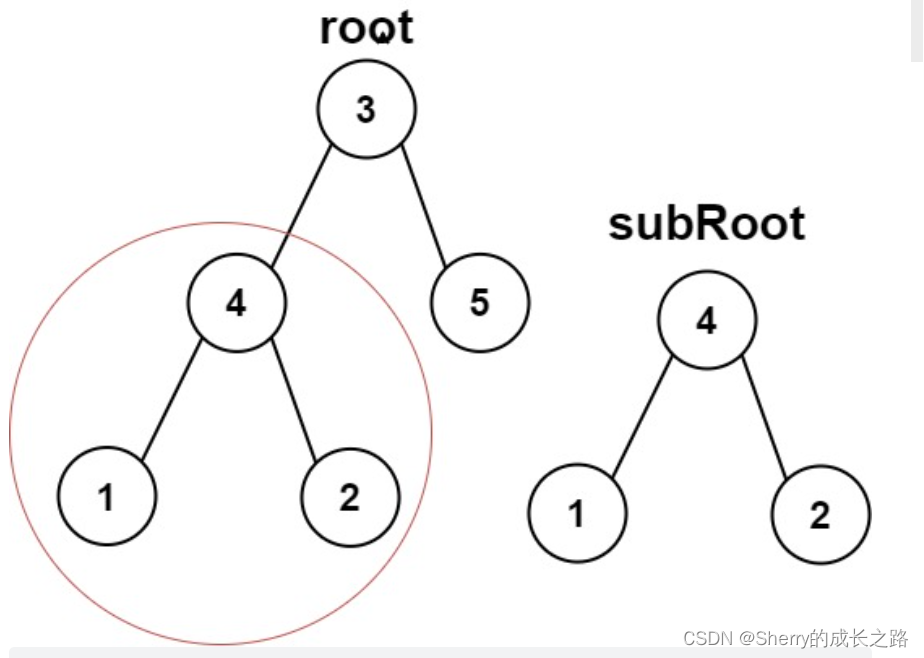
在这里插入图片描述

示例 1：
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true
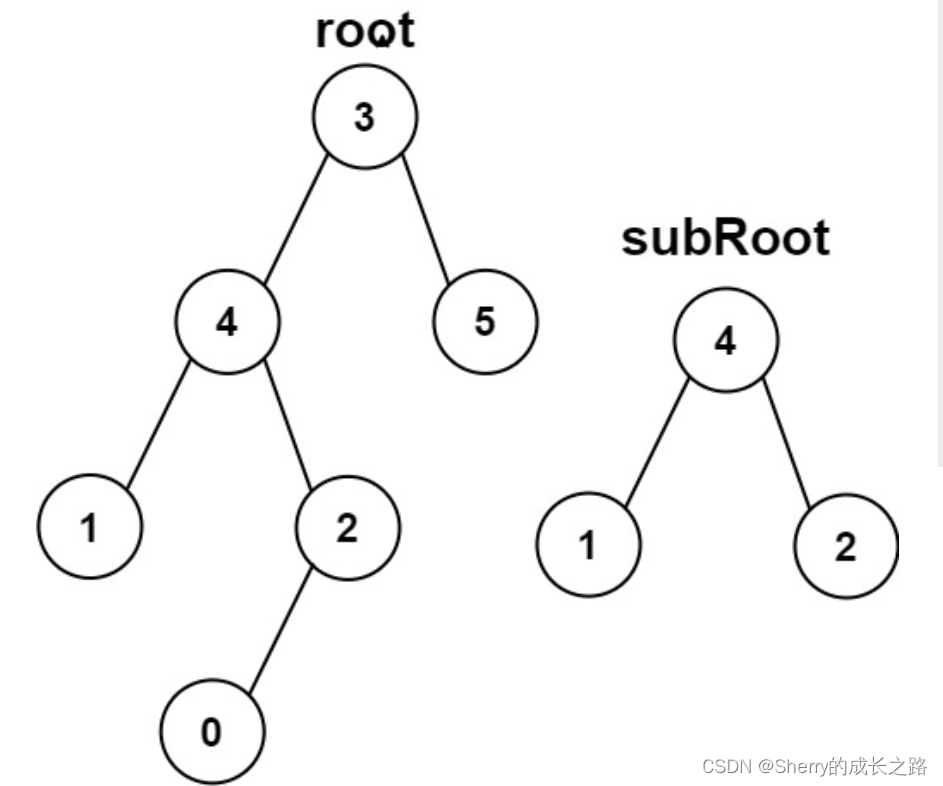
在这里插入图片描述

示例 2：
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

注意：
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

这道题算是 上一篇博客中: 相同的树 的进阶版，如果没有上一题的铺垫，这题会有点难想到。主要思路是判断 二叉树的每一棵子树是否和 subRoot 相等。

由题得，由于 subRoot 一定不为空，所以一旦 root的子树为空，则返回假；
如果 root 的子树 和 subRoot 相等，那么返回真；
否则 递归左右子树，左右子树中任意一边找到了则 子树存在 。
而这里我们判断是否相等就可以直接复用 相同的树 了。

核心思想：每一层函数栈帧中都包括：如果 root 等于空，返回 false；如果调用相同的树为真，返回 true；否则继续递归

//相同的树
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
	//p为空，q也为空
	if (p == NULL && q == NULL)
		return true;
	//p和q只有1个为空
	if (p == NULL || q == NULL)
		return false;
	//p和q的val不等
	if (p->val != q->val)
		return false;
	//相等递归
	return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
//另一棵树的子树
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
	//root等于空
	if (root == NULL)
		return false;
	//调用相同的树
	if (isSameTree(root, subRoot))
		return true;
	//继续递归
	return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

在这里插入图片描述

5、二叉树遍历

链接：二叉树遍历
题述：编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：
输入包括1行字符串，长度不超过 100。

输出描述：
可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

示例 ：

输入：abc##de#g##f###
输出：c b e g d f a

注意此题不同于上面的几道接口题，这里是 I/O 类型的题需要我们自己创建树
根据题意中先序遍历的字符串可以得到：
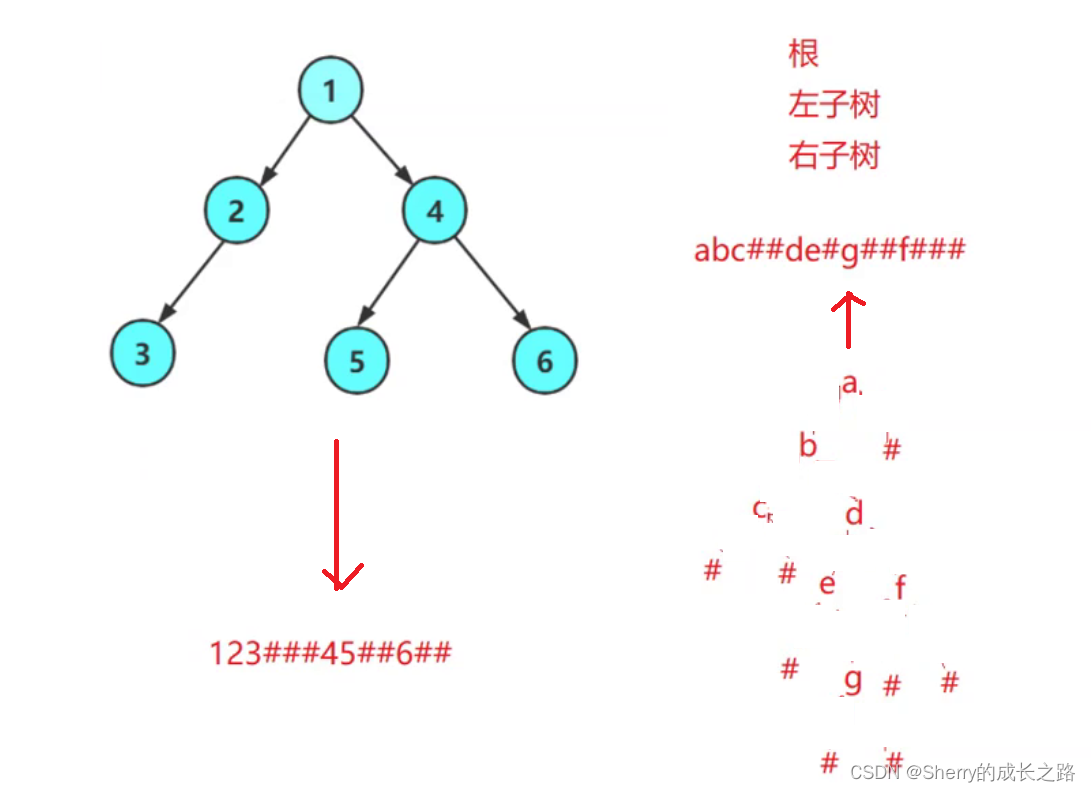
在这里插入图片描述

先前序构建树，再中序输出树

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

struct TreeNode
{
	char val;
	struct TreeNode* left;
	struct TreeNode* right;
};
//前序构建树
struct TreeNode* CreatTree(char* str, int* pi)
{
	if (str[*pi] == '#')
	{
		//空树数组的下标也要++，且为它malloc空间
		(*pi)++;
		return NULL;
	}
	//malloc空间
	struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
	//前序递归
	root->val = str[(*pi)++];
	root->left = CreatTree(str, pi);
	root->right = CreatTree(str, pi);

	return root;
}
//中序输出树
void InOrder(struct TreeNode* root)
{
	if (root == NULL)
		return;
	InOrder(root->left);
	printf("%c ", root->val);
	InOrder(root->right);
}
int main()
{
	char str[100];
	scanf("%s", str);
	int i = 0;
	struct TreeNode* root = CreatTree(str, &i);
	InOrder(root);
	return 0;
}

在这里插入图片描述

6、平衡二叉树

链接：110. 平衡二叉树

描述：给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
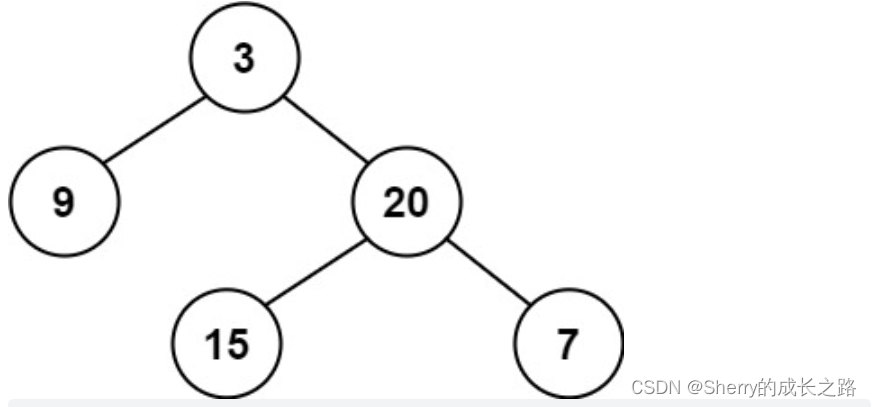
在这里插入图片描述

示例1：
输入：root = [3,9,20,null,null,15,7]
输出：true
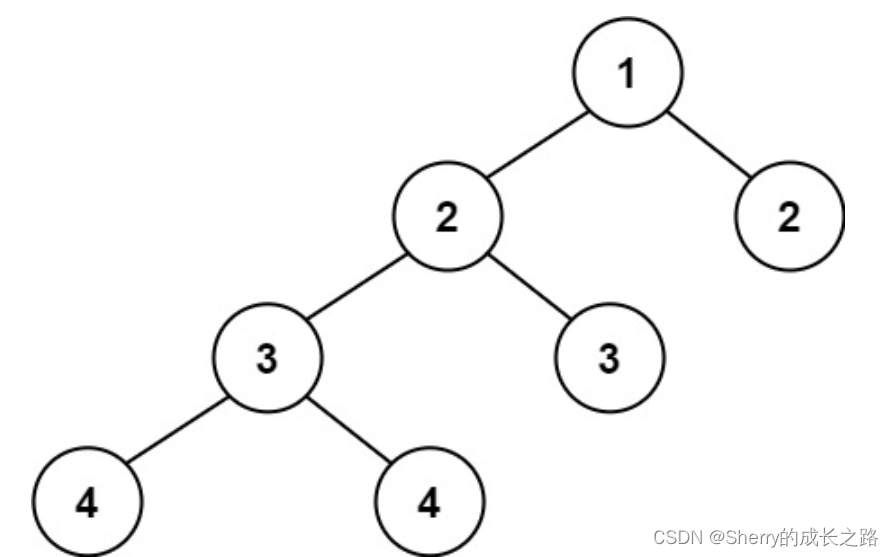
在这里插入图片描述

示例2：
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例3：
输入：root = []
输出：true

提示：
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

思路：
所谓 平衡二叉树就是任意节点的子树的高度差都小于等于1。
基于这个理解，那么我们可以将它分成：每个节点的子树的高度差小于等于1。

那么：
如果节点为空，则是完全二叉树；如果不为空，就求左右两边子树高度；
再判断左右子树的 高度差的绝对值 是否 大于1 ，大于1则一定不是完全二叉树，返回假；
最后分别递归左右子树，判断左右子树是否满足完全二叉树的条件。
求高度可以使用上上篇博客的 计算二叉树的高度 的接口。

//求二叉树的高度 
int TreeHeight(struct TreeNode* root)
{
    if (root == NULL)
    {
        return 0;
    }

    int leftHeight = TreeHeight(root->left);
    int rightHeight = TreeHeight(root->right);

    return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

bool isBalanced(struct TreeNode* root)
{
    // 根节点为空，是完全二叉树
    if (root == NULL)
    {
        return true;
    }

    // 求左右两边高度
    int leftHeight = TreeHeight(root->left);
    int rightHeight = TreeHeight(root->right);

    // 绝对值大于1一定不是完全二叉树
    if (abs(leftHeight - rightHeight) > 1)
    {
        return false;
    }

    return isBalanced(root->left) && isBalanced(root->right);
}

在这里插入图片描述

总结：

今天我们完成了二叉树OJ题(二)，通过分析明白了思路和原理，愿这篇博客能帮助大家理解这些OJ题，到这里，我们的二叉树就暂告一段落啦。接下来将更新排序算法的相关知识点。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~

在这里插入图片描述


http://www.kler.cn/a/7724.html

相关文章：

  • CSS基础知识04
  • vue项目PC端和移动端实现在线预览pptx文件
  • 安全，服务器证书和SSL连接
  • 决策树基本 CART Python手写实现
  • 【LeetCode】【算法】5. 最长回文子串
  • 万字长文解读深度学习——生成对抗网络GAN
  • 精彩回顾 | 平行云亮相LiveVideoStack2022北京站
  • 2023年一个完整的B2B订货网站源码
  • NC65 部门预算DAO类
  • ‘protoc-gen-js‘ 不是内部或外部命令，也不是可运行的程序
  • 在DongshanPI-D1开箱使用分享与折腾记录实现MPU6050数据读取
  • 面向对象编程（基础）8：关键字：package、import
  • 【面试】分库分表15道面试题
  • Python基础（二）
  • 第二章Python序列-列表
  • ROS实践06 自定义消息类型
  • Java基础（一）Java语言概述及入门
  • 【java】java中进制、byte、String转换问题
  • 经济法基础：第二章 会计法律制度
  • QT学习开发笔记（项目实战之智能家居物联 UI 界面开发 ）
  • ftp创建虚拟用户【ftp精细化配置】
  • 编译技术-编译优化
  • 打破传统思维：关键词采集与市场调查的完美结合，引领你的行业领先
  • 优先级队列（java版）
  • SpringBoot 整合 JSP和MyBatis
  • Vue 10 - 计算属性