导数的四则运算
导数的四则运算
- 简单函数
- 复杂函数
简单函数
我们举例14个基本初等函数的函数导数。
| 函数 | 原函数 | 导函数 |
|---|---|---|
| 常函数(即常数) | y = C y=C y=C(C为常数) | y ′ = 0 y'=0 y′=0 |
| 指数函数 | y = a x 、 y = e x y=a^x、y=e^x y=ax、y=ex | y ′ = a x l n a 、 y ′ = e x y'=a^xlna、y'=e^x y′=axlna、y′=ex |
| 幂函数 | y = x n y=x^n y=xn | y ′ = n x n − 1 y'=nx^{n-1} y′=nxn−1 |
| 对数函数 | y = l o g a x 、 y = l n x y=log_a^x、y=lnx y=logax、y=lnx | y ′ = 1 x l n a 、 y ′ = 1 x y'=\frac{1}{xlna}、y'=\frac{1}{x} y′=xlna1、y′=x1 |
| 正弦函数 | s i n x sinx sinx | y ′ = c o s x y'=cosx y′=cosx |
| 余弦函数 | y = c o s x y=cosx y=cosx | y ′ = − c o s x y'=-cosx y′=−cosx |
| 正切函数 | y = t a n x y=tanx y=tanx | y ′ = s e c 2 x y'=sec^2x y′=sec2x |
| 余切函数 | y = c o t x y=cotx y=cotx | y ′ = − c s c 2 x y'=-csc^2x y′=−csc2x |
| 正割函数 | y = s e c x y=secx y=secx | y ′ = s e c x t a n x y'=secxtanx y′=secxtanx |
| 余割函数 | y = c s c x y=cscx y=cscx | y ′ = − c s c x c o t x y'=-cscxcotx y′=−cscxcotx |
| 反正弦函数 | y = a r c s i n x y=arcsinx y=arcsinx | y ′ = 1 1 − x 2 y'=\frac{1}{\sqrt{1-x^2}} y′=1−x21 |
| 反余弦函数 | y = a r c c o s x y=arccosx y=arccosx | y ′ = − 1 1 − x 2 y'=-\frac{1}{\sqrt{1-x^2}} y′=−1−x21 |
| 反正切函数 | a r c t a n x arctanx arctanx | y ′ = 1 1 + x 2 y'=\frac{1}{1+x^2} y′=1+x21 |
| 反余切函数 | a r c c o t x arccotx arccotx | y ′ = − 1 1 + x 2 y'=-\frac{1}{1+x^2} y′=−1+x21 |
| 双曲线函数 | y = s h x y=shx y=shx | y ′ = c h x y'=chx y′=chx |
复杂函数
导数的四则运算如下:
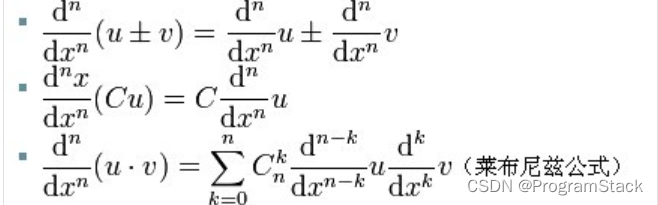
用通俗的方式表示为:
( u ± v ) ′ = u ′ ± v ′ (u\pm v)' = u' \pm v' (u±v)′=u′±v′
( u v ) ′ = u ′ v + u v ′ (uv)'=u'v+uv' (uv)′=u′v+uv′
( u v ) ′ = u ′ v − u v ′ v 2 (\frac{u}{v})' = \frac{u'v-uv'}{v^2} (vu)′=v2u′v−uv′
复合函数对自变量的导数,等于已知函数对中间变量的导数,乘以中间变量对自变量的导数(称为链式法则)。
提示:高阶导数的求法
- 直接法:由高阶导数的定义逐步求高阶导数。一般用来寻找解题方法。
- 高阶导数的运算法则:(牛顿-莱布尼茨公式)
- 间接法:利用已知的高阶导数公式,通过四则运算,变量代换等方法。
注意:代换后函数要便于求,尽量靠拢已知公式求出阶导数。
