类ChatGPT代码级解读:如何从零起步实现Transformer、llama/ChatGLM
前言
最近一直在做类ChatGPT项目的部署 微调,关注比较多的是两个:一个LLaMA,一个ChatGLM,会发现有不少模型是基于这两个模型去做微调的,说到微调,那具体怎么微调呢,因此又详细了解了一下微调代码,发现微调LLM时一般都会用到Hugging face实现的Transformers库的Trainer类
从而发现,如果大家想从零复现ChatGPT,便得从实现Transformer开始,因此便开启了本文:如何从零起步实现Transformer、LLaMA/ChatGLM
且本文的代码解读与其他代码解读最大的不同是:会对出现在本文的每一行代码都加以注释、解释、说明,甚至对每行代码中的变量都会做解释/说明,一如既往的保持对初学者的足够友好,让即便没有太多背景知识的也能顺畅理解本文
第一部分 从零实现Transformer编码器模块
transformer强大到什么程度呢,基本是17年之后绝大部分有影响力模型的基础架构都基于的transformer(比如,这里有200来个,包括且不限于基于decode的GPT、基于encode的BERT、基于encode-decode的T5等等)
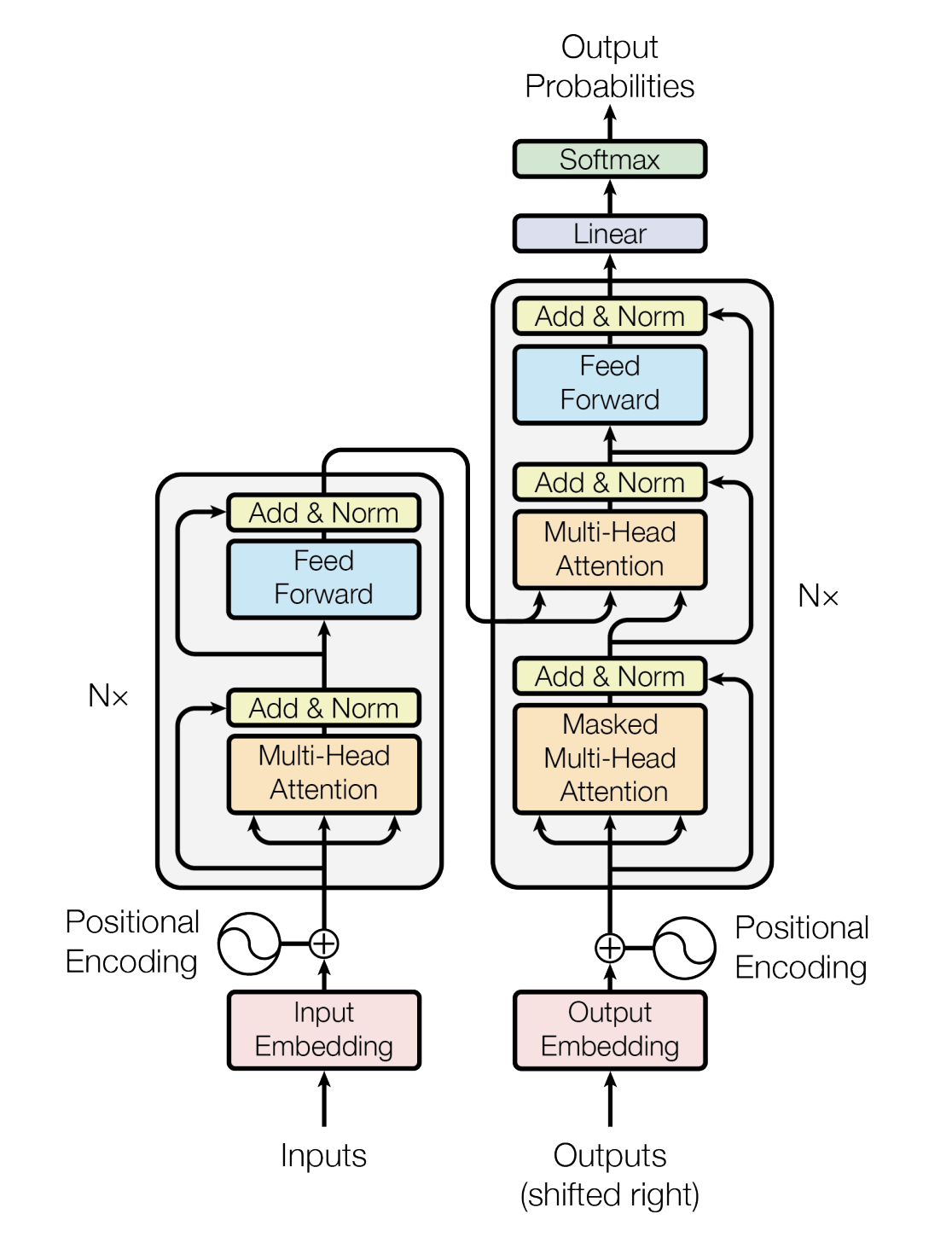
通过博客内的这篇文章《Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT》,我们已经详细了解了transformer的原理(如果忘了,建议必复习下再看本文,当然,如果你实在不想跳转,就只想呆在本文,也行,我努力..)
如果把上图中的各种细节也显示出来,则如下大图所示(此大图来源于七月在线NLP11里倪老师讲的Transformer模型源码解读)
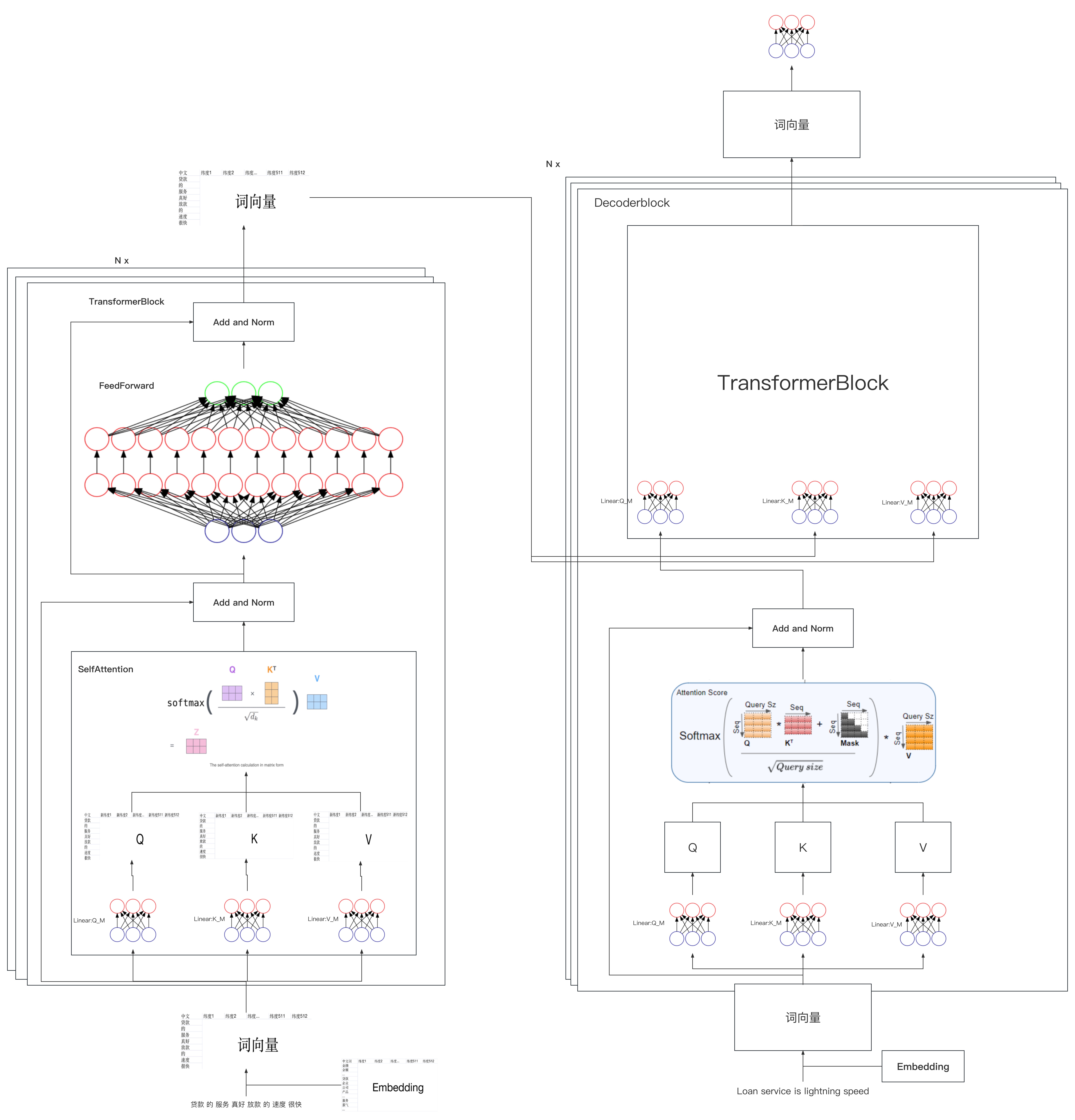
考虑到Hugging face实现的Transformers库虽然功能强大,但3000多行,对于初次实现的初学者来说,理解难度比较大,因此,咱们一步步结合对应的原理来逐行编码实现一个简易版的transformer
1.1 关于输入的处理:针对输入做embedding,然后加上位置编码
首先,先看上图左边的transformer block里,input先embedding,然后加上一个位置编码
1.1.1 针对输入做embedding
这里值得注意的是,对于模型来说,每一句话比如“七月的服务真好,答疑的速度很快”,在模型中都是一个词向量,但如果每句话都临时抱佛脚去生成对应的词向量,则处理起来无疑会费时费力,所以在实际应用中,我们会事先预训练好各种embedding矩阵,这些embedding矩阵包含常用领域常用单词的向量化表示,且提前做好分词
| 教育 | 维度1 | 维度2 | 维度3 | 维度4 | ... | 维度512 |
| 机构 | ||||||
| 在线 | ||||||
| 课程 | ||||||
| .. | ||||||
| 服务 | ||||||
| 答疑 | ||||||
| 老师 | ||||||
| .. |
从而当模型接收到“七月的服务真好,答疑的速度很快”这句输入时,便可以从对应的embedding矩阵里查找对应的词向量,最终把整句输入转换成对应的向量表示
1.1.2 位置编码的深意:如何编码更好
然,如此篇文章所述,RNN的结构包含了序列的时序信息,而Transformer却完全把时序信息给丢掉了,比如“他欠我100万”,和“我欠他100万”,两者的意思千差万别,故为了解决时序的问题,Transformer的作者用了一个绝妙的办法:位置编码(Positional Encoding)。
即将每个位置编号,从而每个编号对应一个向量,最终通过结合位置向量和词向量,作为输入embedding,就给每个词都引入了一定的位置信息,这样Attention就可以分辨出不同位置的词了,具体怎么做呢?
- 如果简单粗暴的话,直接给每个向量分配一个数字,比如1到1000之间
- 也可以用one-hot编码表示位置,可以发现,每个比特位的变化率是不一样的,越低位的变化越快,红色位置0和1每个数字会变化一次,而黄色位,每8个数字才会变化一次

- 更可以把位置向量当中的每一个元素都用一个sin函数来表示,则第t个token的位置向量可以表示为:
举个例子,如下图,类似调收音机的旋转按钮调声量一样,第一个刻度盘将调整音量非常小,可能是 1 个单位,几乎听不见差异。第二个会更强大,将音量调整 2 个单位。第三个将调整 4 个单位,第四个调整 8 个单位,依此类推
通过频率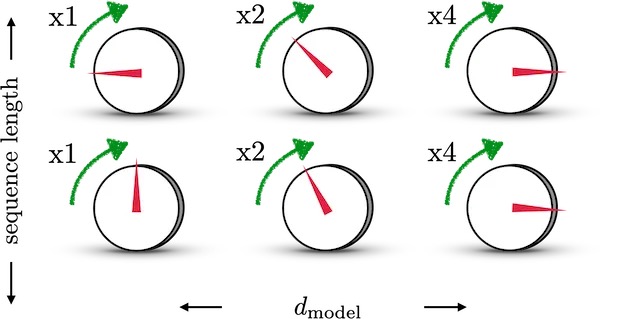
来控制sin函数的波长,频率不断减小,则波长不断变大,此时sin函数对t的变动越不敏感,以此来达到越向右的旋钮,指针移动步伐越小的目的。 这也类似于二进制编码,每一位上都是0和1的交互,越往低位走(越往左边走),交互的频率越慢
- transformer论文中作者探索了两种创建 positional encoding 的方法:
通过训练学习 positional encoding 向量
使用公式来计算 positional encoding向量,试验后发现两种选择的结果是相似的,所以采用了第2种方法,优点是不需要训练参数,而且即使在训练集中没有出现过的句子长度上也能用,计算positional encoding的公式
咋一看,这两个公式可能不太好理解,没关系,我们来拆解下pos 表示token在sequence中的位置,例如第一个token的pos为0
代表位置向量的维度(也是词embedding的维度),2i 表示偶数的维度,2i+1 表示奇数维度 『其中i的取值范围为
,且 2i≤d, 2i+1≤d』
举个例子,i 可以是0,1,2,...383
2i 是指向量维度中的偶数维,即第0维,第2维,第4维,直到第766维,用正弦函数计算
2i+1 是维度中的奇数维,即第1维,第3维,第5维,直到第767维,用余弦函数计算
// 截止到4.14日,这个transformer的位置编码还有一些细节没有讲透彻,待进一步补充完善
代码实现如下
‘’‘位置编码的实现,调用父类nn.Module的构造函数’‘’
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout) # 初始化dropout层
# 计算位置编码并将其存储在pe张量中
pe = torch.zeros(max_len, d_model) # 创建一个max_len x d_model的全零张量
position = torch.arange(0, max_len).unsqueeze(1) # 生成0到max_len-1的整数序列,并添加一个维度
# 计算div_term,用于缩放不同位置的正弦和余弦函数
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
# 使用正弦和余弦函数生成位置编码。对于d_model的偶数索引,使用正弦函数;对于奇数索引,使用余弦函数。
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # 在第一个维度添加一个维度,以便进行批处理
self.register_buffer('pe', pe) # 将位置编码张量注册为缓冲区,以便在不同设备之间传输模型时保持其状态
# 定义前向传播函数
def forward(self, x):
# 将输入x与对应的位置编码相加
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
# 应用dropout层并返回结果
return self.dropout(x)1.2 经过「embedding + 位置编码」后乘以三个权重矩阵得到三个向量Q K V
从下图可知,经过「embedding + 位置编码」得到的输入,会乘以「三个权重矩阵:
」得到查询向量q、键向量k、值向量v(你可以简单粗暴的理解为弄出来了三个分身),然后做下线性变换
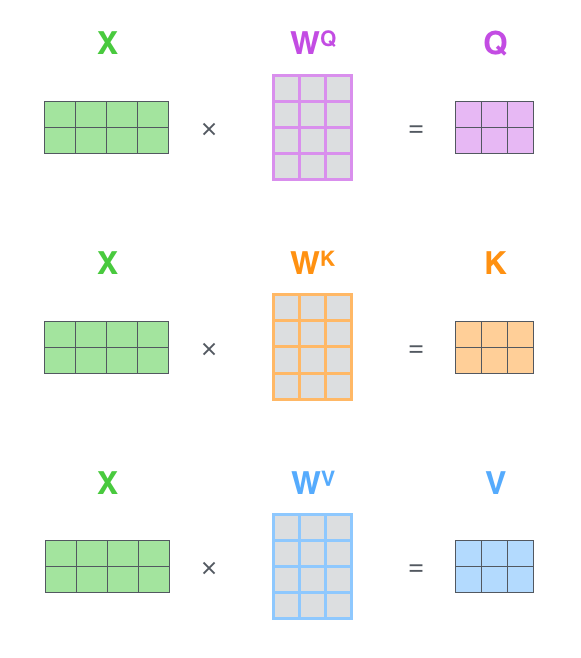
为此,我们可以先创建四个相同的线性层,每个线性层都具有 d_model 的输入维度和 d_model 的输出维度
self.linears = clones(nn.Linear(d_model, d_model), 4) 前三个线性层分别用于对 q向量、k向量、v 向量进行线性变换(至于这第4个线性层在随后的第3点)
1.3 对输入和Multi-Head Attention做Add&Norm,再对上步输出和Feed Forward做Add&Norm
我们聚焦下transformer论文中原图的这部分,可知,输入通过embedding+位置编码后,先做以下两个步骤
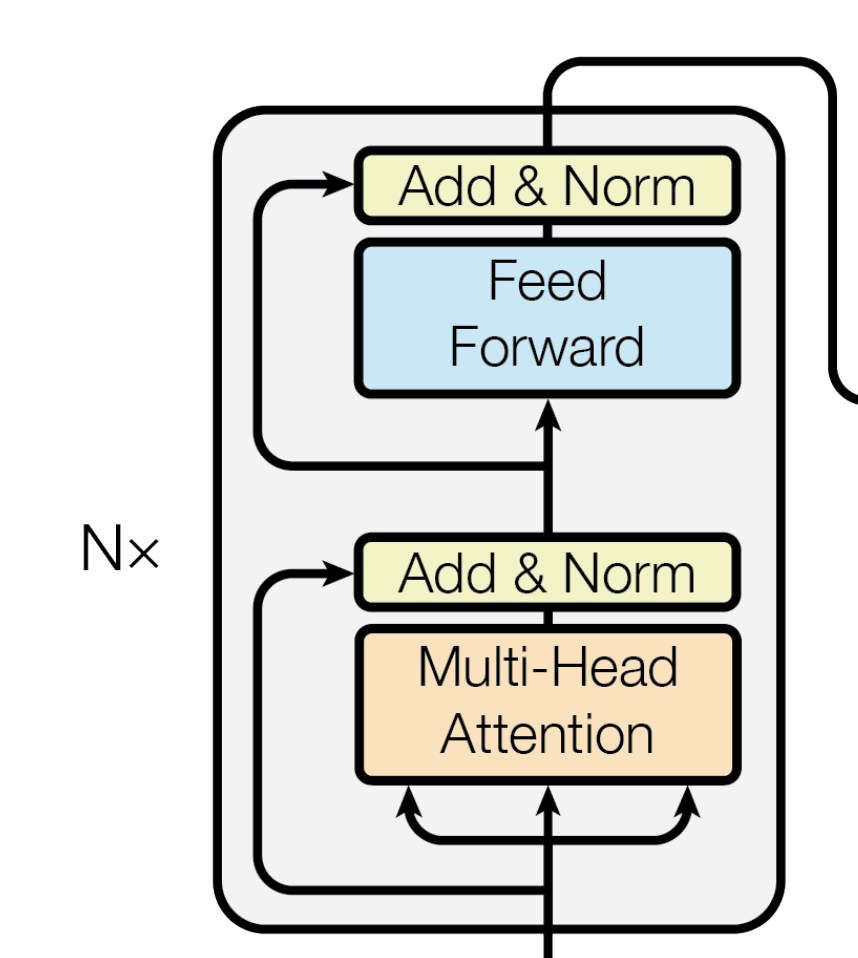
- 针对query向量做multi-head attention,得到的结果与原query向量,做相加并归一化
这个相加具体是怎么个相加法呢?事实上,Add代表的Residual Connection(残差连接),是为了解决多层神经网络训练困难的问题,通过将前一层的信息无差的传递到下一层,可以有效的仅关注差异部分,这一方法之前在图像处理结构如ResNet等中常常用到attention = self.attention(query, key, value, mask) output = self.dropout(self.norm1(attention + query))
具体编码时通过 SublayerConnection 函数实现此功能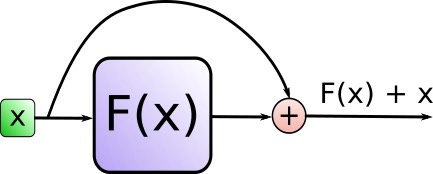
而Norm则代表了Layer Normalization,通过对层的激活值的归一化,可以加速模型的训练过程,使其更快的收敛,编码时用 LayerNorm 函数实现"""一个残差连接(residual connection),后面跟着一个层归一化(layer normalization)操作""" class SublayerConnection(nn.Module): # 初始化函数,接收size(层的维度大小)和dropout(dropout率)作为输入参数 def __init__(self, size, dropout): super(SublayerConnection, self).__init__() # 调用父类nn.Module的构造函数 self.norm = LayerNorm(size) # 定义一个层归一化(Layer Normalization)操作,使用size作为输入维度 self.dropout = nn.Dropout(dropout) # 定义一个dropout层 # 定义前向传播函数,输入参数x是输入张量,sublayer是待执行的子层操作 def forward(self, x, sublayer): # 将残差连接应用于任何具有相同大小的子层 # 首先对输入x进行层归一化,然后执行子层操作(如self-attention或前馈神经网络) # 接着应用dropout,最后将结果与原始输入x相加。 return x + self.dropout(sublayer(self.norm(x)))'''构建一个层归一化(layernorm)模块''' class LayerNorm(nn.Module): # 初始化函数,接收features(特征维度大小)和eps(防止除以零的微小值)作为输入参数 def __init__(self, features, eps=1e-6): super(LayerNorm, self).__init__() # 调用父类nn.Module的构造函数 self.a_2 = nn.Parameter(torch.ones(features)) # 定义一个大小为features的一维张量,初始化为全1,并将其设置为可训练参数 self.b_2 = nn.Parameter(torch.zeros(features)) # 定义一个大小为features的一维张量,初始化为全0,并将其设置为可训练参数 self.eps = eps # 将防止除以零的微小值eps保存为类实例的属性 # 定义前向传播函数,输入参数x是输入张量 def forward(self, x): mean = x.mean(-1, keepdim=True) # 计算输入x在最后一个维度上的均值,保持输出结果的维度 std = x.std(-1, keepdim=True) # 计算输入x在最后一个维度上的标准差,保持输出结果的维度 # 对输入x进行层归一化,使用可训练参数a_2和b_2进行缩放和偏移,最后返回归一化后的结果 return self.a_2 * (x - mean) / (std + self.eps) + self.b_2 - 上面步骤得到的『输出结果output做feed forward』之后,再与『上面步骤的原输出结果output』也做相加并归一化
forward = self.feed_forward(output) block_output = self.dropout(self.norm2(forward + output)) return block_output
这个编码器层代码可以完整的写为
"""编码器(Encoder)由自注意力(self-attention)层和前馈神经网络(feed forward)层组成"""
class EncoderLayer(nn.Module):
# 初始化函数,接收size(层的维度大小)、self_attn(自注意力层实例)、feed_forward(前馈神经网络实例)和dropout(dropout率)作为输入参数
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__() # 调用父类nn.Module的构造函数
self.self_attn = self_attn # 将自注意力层实例保存为类实例的属性
self.feed_forward = feed_forward # 将前馈神经网络实例保存为类实例的属性
self.sublayer = clones(SublayerConnection(size, dropout), 2) # 创建两个具有相同参数的SublayerConnection实例(用于残差连接和层归一化)
self.size = size # 将层的维度大小保存为类实例的属性
# 先对输入x进行自注意力操作,然后将结果传递给第一个SublayerConnection实例(包括残差连接和层归一化)
def forward(self, x, mask):
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
# 将上一步的输出传递给前馈神经网络,然后将结果传递给第二个SublayerConnection实例(包括残差连接和层归一化),最后返回结果
return self.sublayer[1](x, self.feed_forward)1.3.1 缩放点积注意力(Scaled Dot-Product Attention)
接下来,先看下缩放点积注意力(Scaled Dot-Product Attention)的整体实现步骤
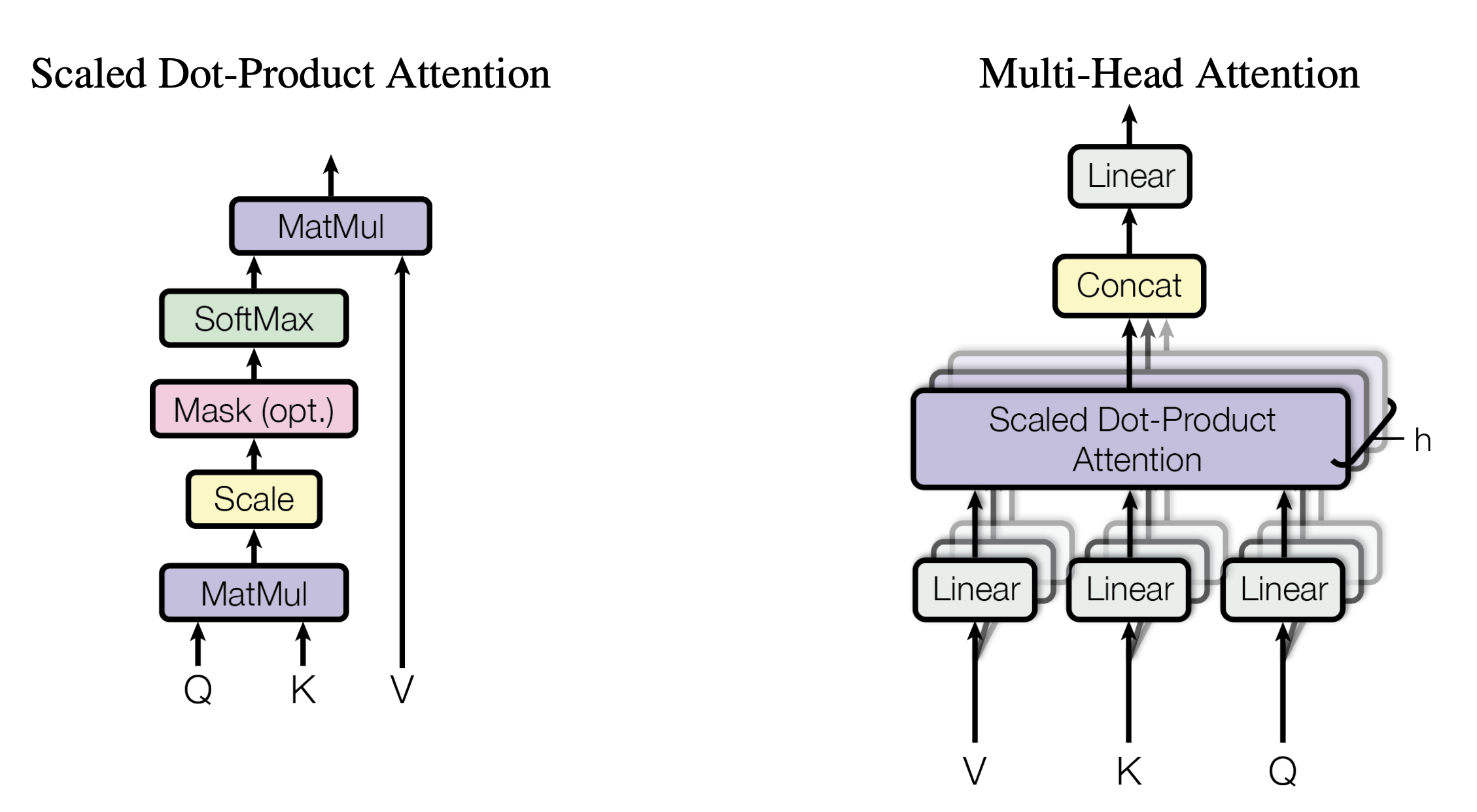
- 为了计算每个单词与其他单词之间的相似度,会拿「每个单词/token的q向量」与「包括自身在内所有单词/token的k向量」一一做点积(两个向量之间的点积结果可以代表两个向量的相似度)
对应到矩阵的形式上,则是矩阵Q与K矩阵的转置做相乘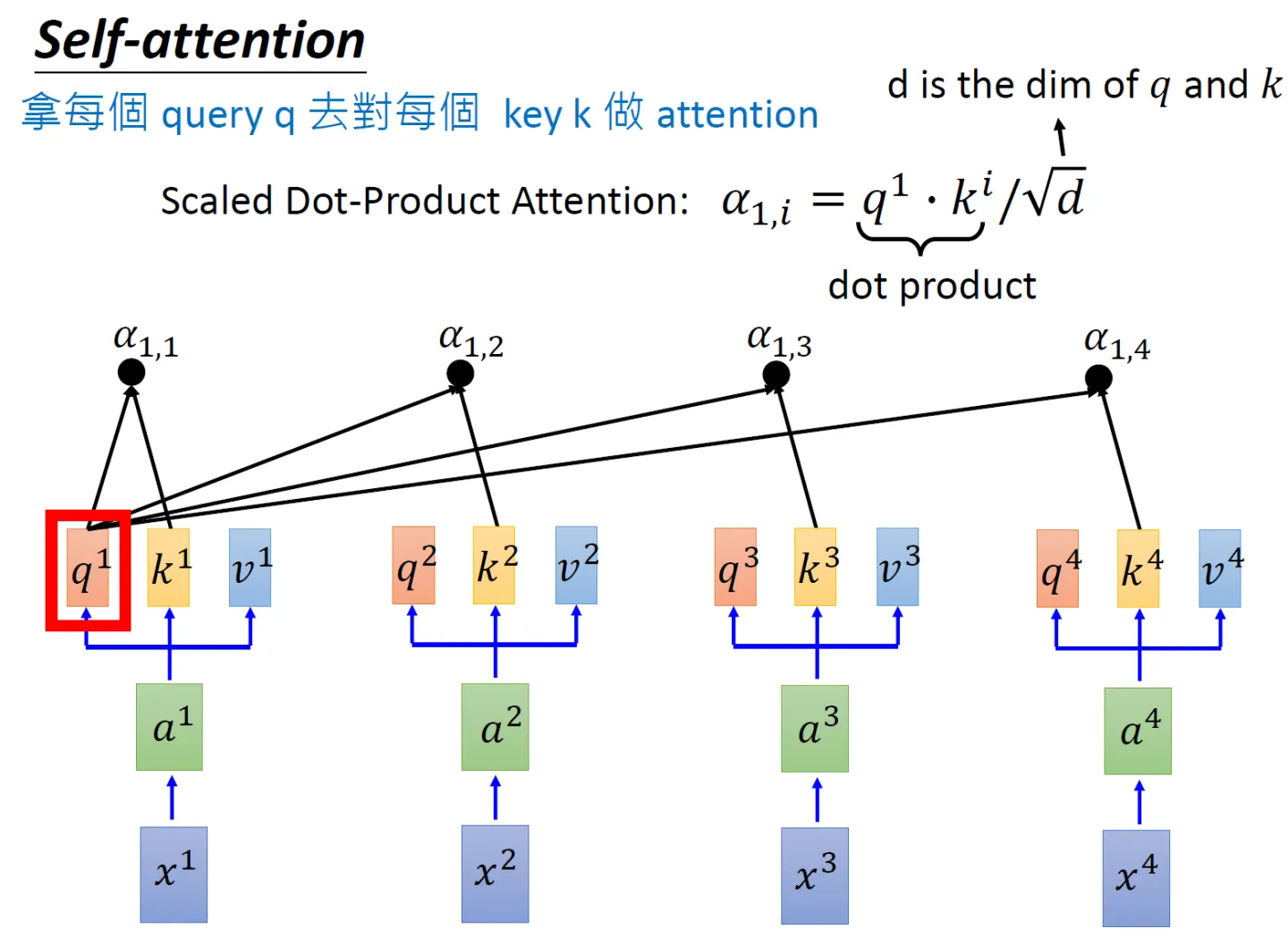
举个例子,假设一个句子中的单词是:1 2 3 4,则Q乘以K的转置如下图所示
最终得到的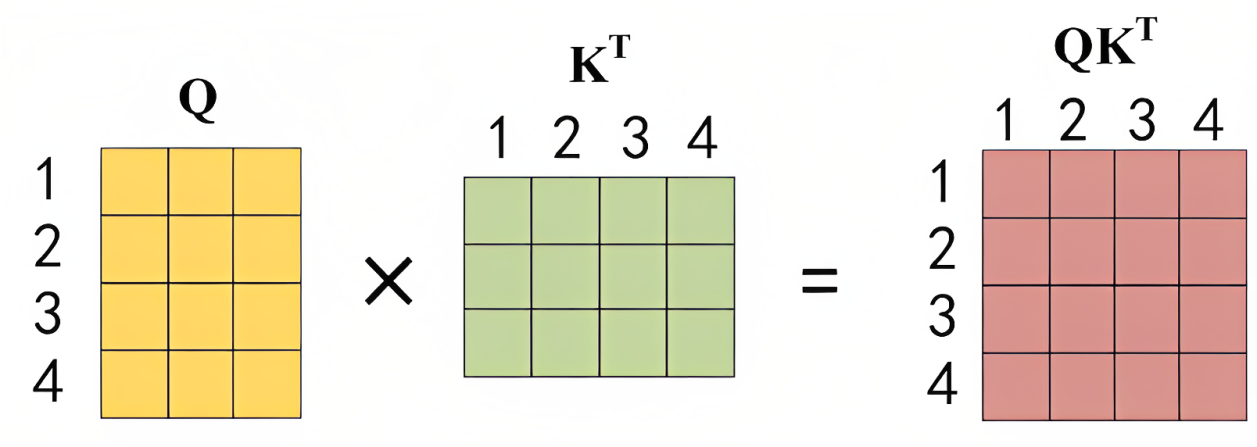
矩阵有4行4列,从上往下逐行来看的话,每一个格子里都会有一个数值,每一个数值依次代表:
单词1与1 2 3 4各自的点积结果或相似度,比如可能是0.5 0.2 0.2 0.1,代表编码1时放在1 2 3 4上面的注意力大小
同时,可以看到模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置(当然 这无可厚非,毕竟自己与自己最相似嘛),而可能忽略了其它位置。很快你会看到,作者采取的一种解决方案就是采用多头注意力机制(Multi-Head Attention)2与1 2 3 4各自的点积结果或相似度
3与1 2 3 4各自的点积结果或相似度
4与1 2 3 4各自的点积结果或相似度
- 由于
会随着dimension的增大而增大,为避免过大,所以除以
,相当于对点积的结果做下缩放
其中,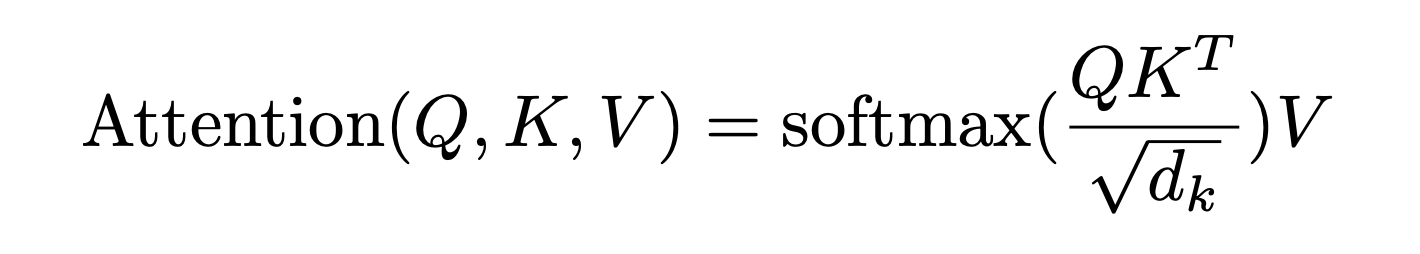
是向量
的维度,且
,如果只设置了一个头,那
就是模型的维度
,如果设置了8个头,则
,且模型的维度是512维,则
即等于8
上面两步的代码可以如下编写# torch.matmul是PyTorch库提供的矩阵乘法函数 # 具体操作即是将第一个矩阵的每一行与第二个矩阵的每一列进行点积(对应元素相乘并求和),得到新矩阵的每个元素 scores = torch.matmul(query, key.transpose(-2, -1)) \ / math.sqrt(d_k) - 接着使用 Softmax 计算每一个单词对于其他单词的 Attention值,这些值加起来的和为1(相当于起到了归一化的效果)
这步对应的代码为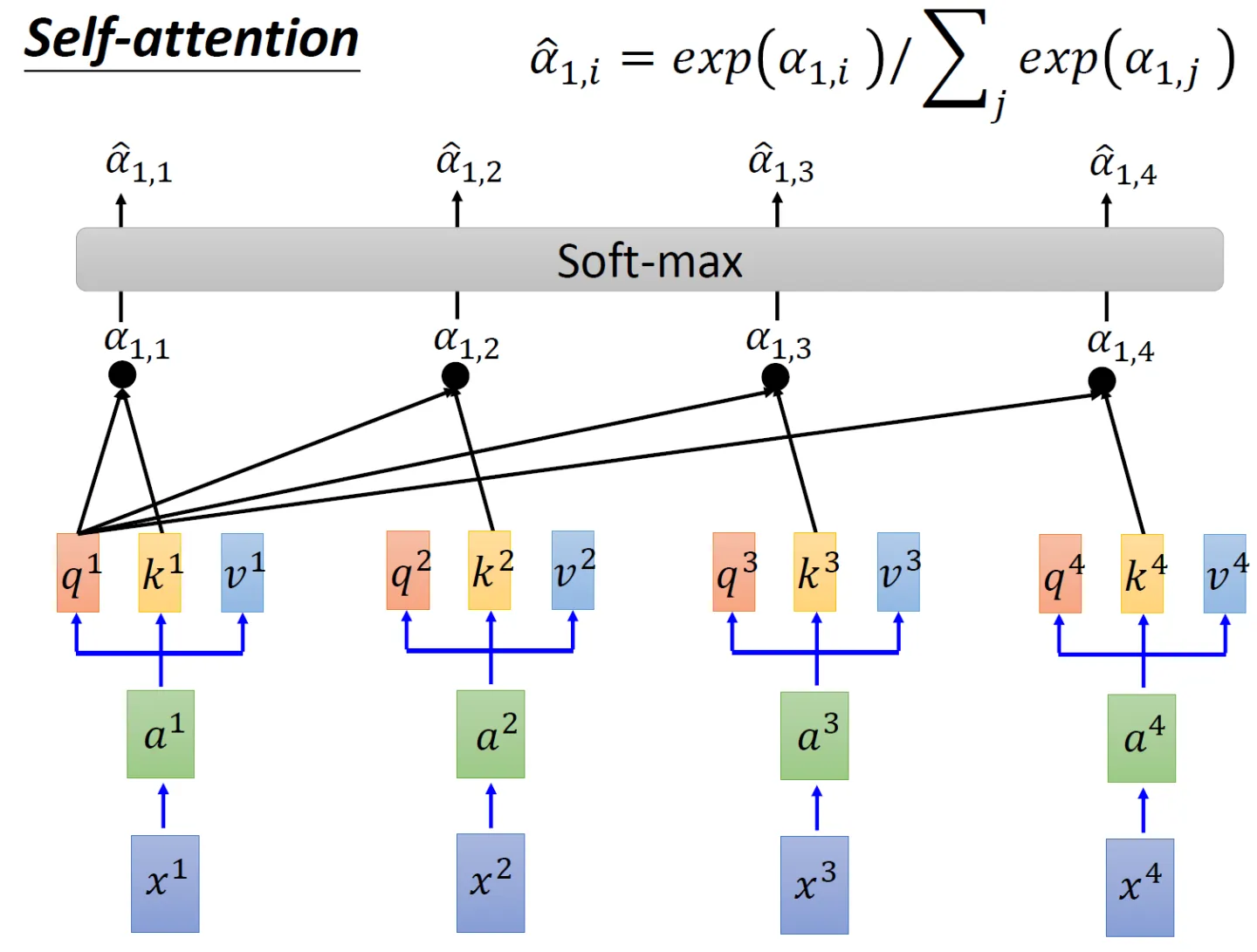
# 对 scores 进行 softmax 操作,得到注意力权重 p_attn p_attn = F.softmax(scores, dim = -1) - 最后再乘以
矩阵,即对所有values(v1 v2 v3 v4),根据不同的attention值(
),做加权平均
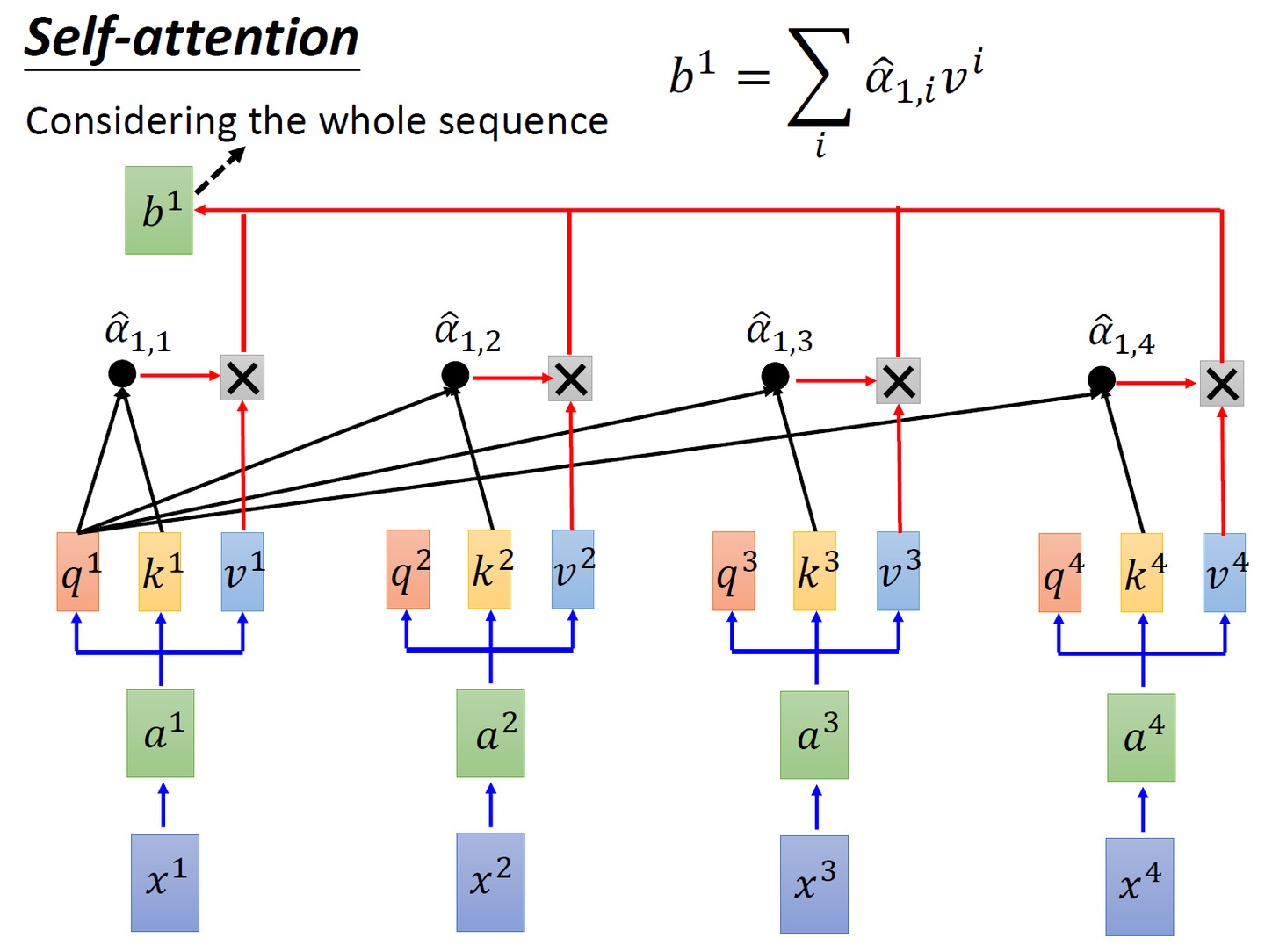
- 最终得到单词的输出,如下图所示(图中V矩阵的4行分别代表v1 v2 v3 v4):
上述两步对应的代码为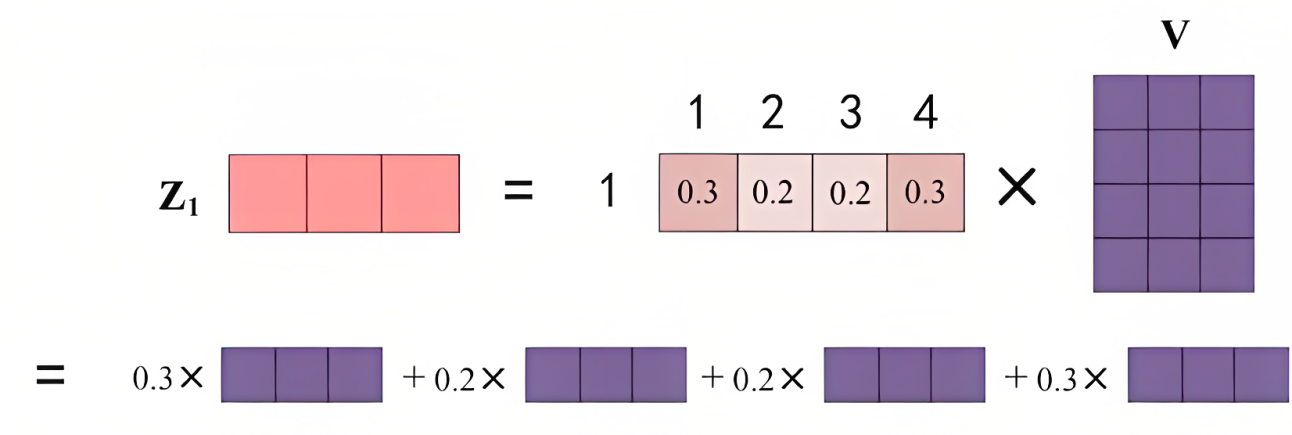
# 用注意力权重 p_attn 对 value 向量进行加权求和,得到最终的输出 return torch.matmul(p_attn, value), p_attn
最终,Scaled Dot-Product Attention这部分对应的完整代码可以写为
'''计算“缩放点积注意力'''
# query, key, value 是输入的向量组
# mask 用于遮掩某些位置,防止计算注意力
# dropout 用于添加随机性,有助于防止过拟合
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1) # 获取 query 向量的最后一个维度的大小,即词嵌入的维度
# 计算 query 和 key 的点积,并对结果进行缩放,以减少梯度消失或爆炸的可能性
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
# 如果提供了 mask,根据 mask 对 scores 进行遮掩
# 遮掩的具体方法就是设为一个很大的负数比如-1e9,从而softmax后 对应概率基本为0
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 对 scores 进行 softmax 操作,得到注意力权重 p_attn
p_attn = F.softmax(scores, dim = -1)
# 如果提供了 dropout,对注意力权重 p_attn 进行 dropout 操作
if dropout is not None:
p_attn = dropout(p_attn)
# 用注意力权重 p_attn 对 value 向量进行加权求和,得到最终的输出
return torch.matmul(p_attn, value), p_attn1.3.2 多头注意力(Multi-Head Attention)
先看2个头的例子,依然还是通过生成对应的三个矩阵
、
、
,然后这三个矩阵再各自乘以两个转移矩阵得到对应的分矩阵,如
矩阵对应的两个分矩阵
、
矩阵对应的两个分矩阵为
、
矩阵对应的两个分矩阵为
、
至于同理,也生成对应的6个分矩阵
、
、
、
、
、
接下来编码时,分两步
先与
做点积然后乘以
,然后再与
做点积再乘以
,再把这两个计算的结果相加得到
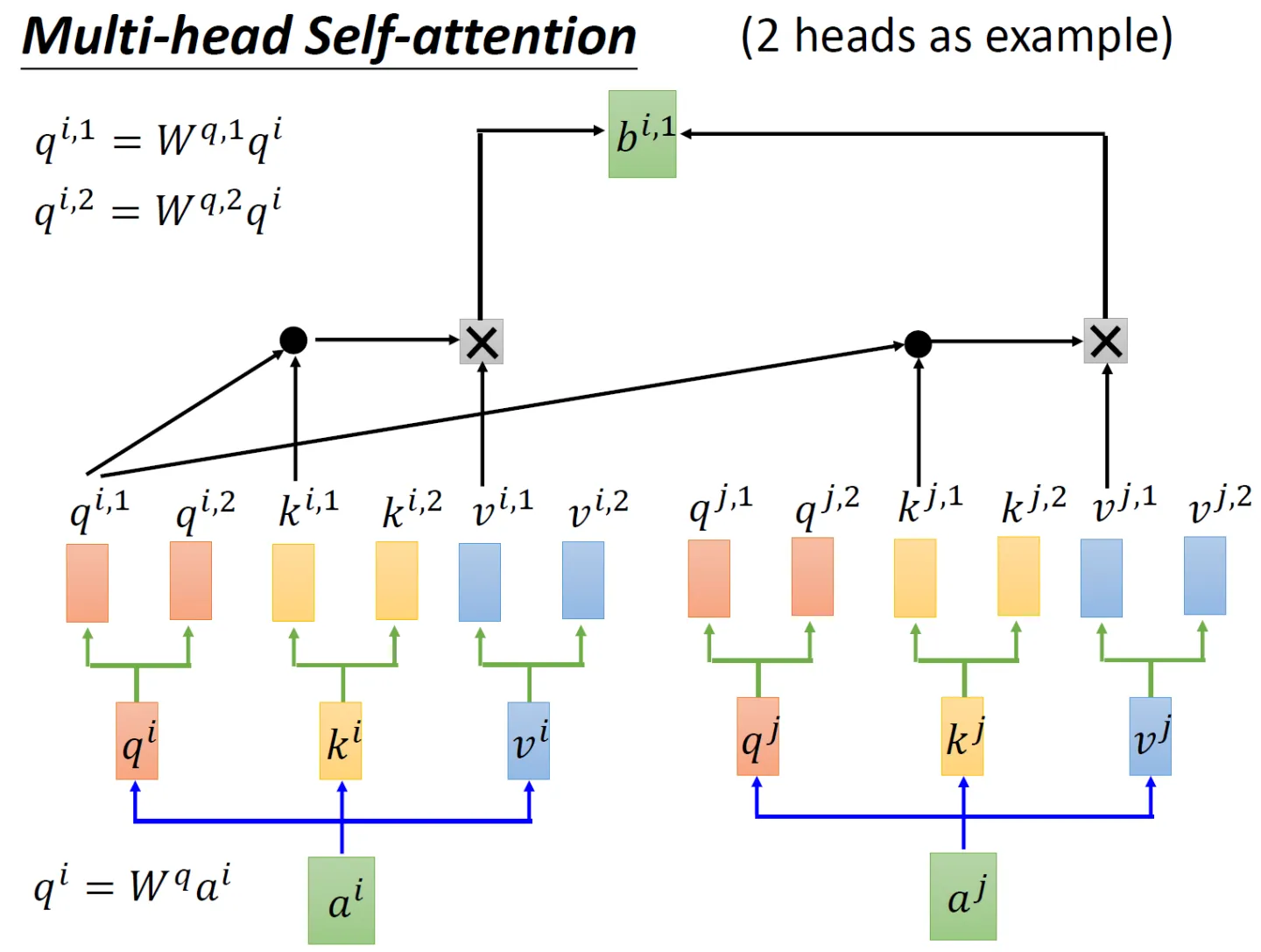
再分别与
做点积然后乘以
、然后再与
做点积再乘以
,再把这两个计算的结果相加得到

如果是8个头呢,计算步骤上也是一样的,只是从2个头变化到8个头而已,最终把每个头得到的结果直接concat,最后经过一个linear变换,得到最终的输出,整体如下所示
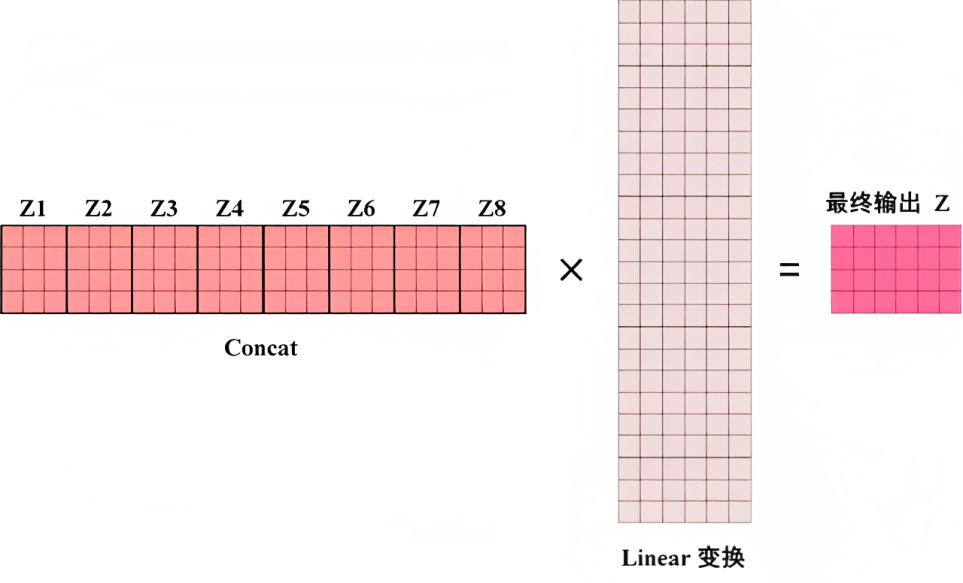
这部分Multi-Head Attention的代码可以写为
'''代码来自nlp.seas.harvard.edu,我针对每一行代码、甚至每行代码中的部分变量都做了详细的注释/解读'''
class MultiHeadedAttention(nn.Module):
# 输入模型的大小(d_model)和注意力头的数量(h)
def __init__(self, h, d_model, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0 # 确保 d_model 可以被 h 整除
# 我们假设 d_v(值向量的维度)总是等于 d_k(键向量的维度)
self.d_k = d_model // h # 计算每个注意力头的维度
self.h = h # 保存注意力头的数量
self.linears = clones(nn.Linear(d_model, d_model), 4) # 上文解释过的四个线性层
self.attn = None # 初始化注意力权重为 None
self.dropout = nn.Dropout(p=dropout) # 定义 dropout 层
# 实现多头注意力的前向传播
def forward(self, query, key, value, mask=None):
if mask is not None:
# 对所有 h 个头应用相同的 mask
mask = mask.unsqueeze(1)
nbatches = query.size(0) # 获取 batch 的大小
# 1) 批量执行从 d_model 到 h x d_k 的线性投影
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) 在批量投影的向量上应用注意力
# 具体方法是调用上面实现Scaled Dot-Product Attention的attention函数
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) 使用 view 函数进行“拼接concat”,然后做下Linear变换
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x) # 返回多头注意力的输出1.3.3 Position-wise前馈网络的实现
在上文,咱们逐一编码实现了embedding、位置编码、缩放点积/多头注意力,以及Add和Norm,整个编码器部分还剩最后一个模块,即下图框里的Feed Forward Network(简称FFN)
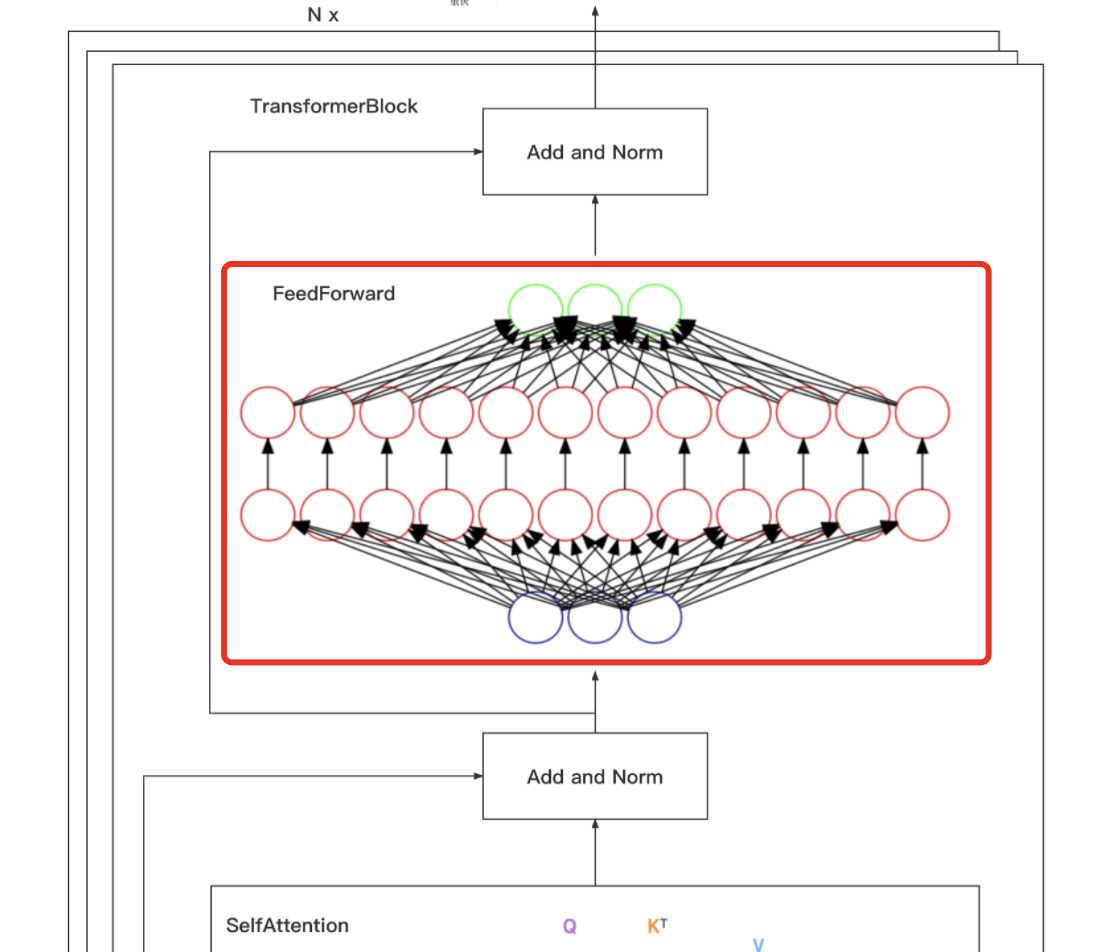
其中包括两个线性变换:维度上先扩大后缩小,最终输入和输出的维数为,内层的维度为
,过程中使用ReLU作为激活函数
虽然线性变换在不同位置上是相同的,但它们在层与层之间使用不同的参数,相当于使用了两个内核大小为1的卷积
这部分的代码可以如下编写
‘’‘定义一个名为PositionwiseFeedForward的类,继承自nn.Module’‘’
class PositionwiseFeedForward(nn.Module):
# 文档字符串:实现FFN方程
# 初始化方法,接受三个参数:d_model,d_ff和dropout(默认值为0.1)
def __init__(self, d_model, d_ff, dropout=0.1):
# 调用父类nn.Module的初始化方法
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff) # 定义一个全连接层,输入维度为d_model,输出维度为d_ff
self.w_2 = nn.Linear(d_ff, d_model) # 定义一个全连接层,输入维度为d_ff,输出维度为d_model
self.dropout = nn.Dropout(dropout) # 定义一个dropout层,dropout概率为传入的dropout参数
# 定义前向传播方法,接受一个输入参数x
def forward(self, x):
# 将输入x通过第一个全连接层w_1后,经过ReLU激活函数,再通过dropout层,最后通过第二个全连接层w_2,返回最终结果
return self.w_2(self.dropout(F.relu(self.w_1(x))))第二部分 从零实现Transformer解码器模块
// 待更
第三部分 LLaMA与ChatGLM-6B的代码架构与逐一实现
// 待更..
第四部分 如何加速模型的训练以及调优
// 本文正在每天更新中,预计4月底完成初稿,5月底基本成型..
参考文献与推荐阅读
- Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT
- Transformer原始论文(值得反复读几遍):Attention Is All You Need
- Vision Transformer 超详细解读 (原理分析+代码解读) (一)
- Transformer模型详解(图解最完整版)
- The Annotated Transformer(翻译之一),harvard对transformer的简单编码实现
- transformer的细节到底是怎么样的?
- 如何从浅入深理解transformer?
- Transformer 结构详解:位置编码 | Transformer Architecture: The Positional Encoding
- Transformer学习笔记一:Positional Encoding(位置编码)
附录:创作/修改记录
- 4.12-4.14,基本完成第一部分 transformer编码器部分的初稿
- ..