matlab simulink 直线一级倒立摆控制(自起摆和稳态控制)
1、内容简介
略
6-可以交流、咨询、答疑
2、内容说明
- 控制器设计
- 自起摆建模
规定正方向:顺时针为角度(力矩)正方向,向右为位移正方向。
在规定的正方向条件下,图 1 所示摆杆的角度φ为正值, 下车向右加速,故a为正值,则摆杆相对于小车的运动方程可表示为:
其中,J是指摆杆相对于摆杆转轴的转动惯量,
若垂直向下位置规定为π,则有:
由此可见,当正方向确定后,摆杆运动方程的形式与摆杆垂直向下位置的
规定角度无关。同理,假如开始时小车向左加速,摆杆向右摆起,,可得摆杆运动方程与上述相同。
-
- 自起摆算法设计与仿真
利用李雅谱诺夫原理构建控制律
由前面的分析可知,倒立摆摆杆的运动方程为:
,可改写成:
。
摆杆的能量可以由两部分构成:转动动能和势能,若将摆杆垂直向上位置的势能定义为零势能,则摆杆的能量Ep可表示为:
(1)
摆杆的目标位置是垂直向上,且摆起后的理想状态是,
均为0。由此可知,在摆起过程中,
(摆杆垂直向下位置),
(摆杆垂直向上位置),理想的控制率应保证
在摆起过程汇总始终是减小的。
小车在运动过程中的能量
, 由于在控制摆杆摆起到目标位置的同时,小车的横向位置应回到起摆时的位置,在构建小车的能量函数时应考虑小车的位移,为此,构建小车的广义能量函数为:
, 为了简
化后继的运算,与摆杆的能量函数之间能提取出公共项,引入一个比例系数r将
表达为:
。
构建一个李雅谱诺夫函数如下:
(2)
,其中
表示取
的符号。
为了确保
,取控制量
为如下形式:
(3)
其中α为权重系数,其值的选取是保证控制量
在许可的范围之内,保证系统尽可能快地收敛(达到目标值)。
当
时,除了在垂直向上位置,即倒立摆系统处于平衡位置
时,均有下式成立:
由此可知,当
取(3)所示的值时,系统在平衡位置是渐进稳定的,摆杆能摆起至垂直向上位置。
在实际运算中,当
时,系统将无法运算,为了防止该种情况发生,在实际控制时,可采用以下控制规律:
实际仿真中,取
。仿真步长设定为0.01s。

3、仿真分析
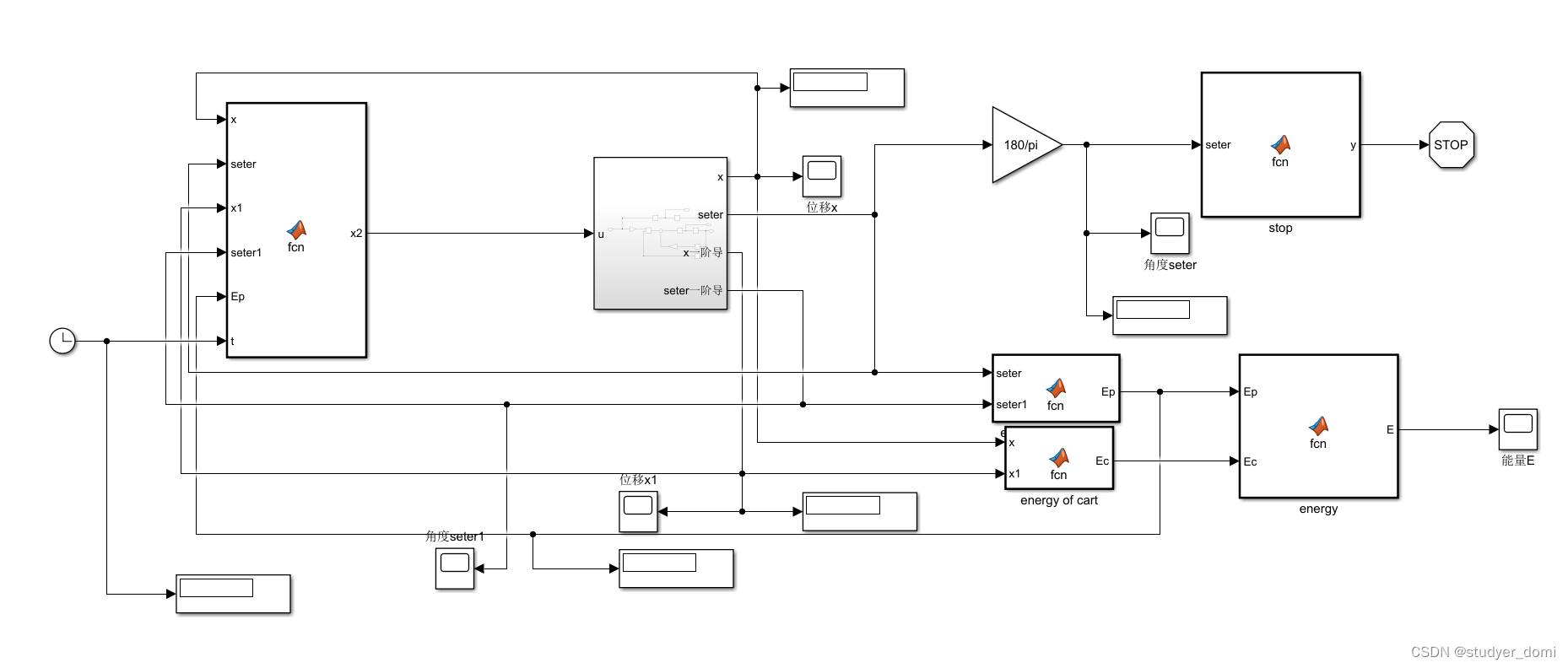
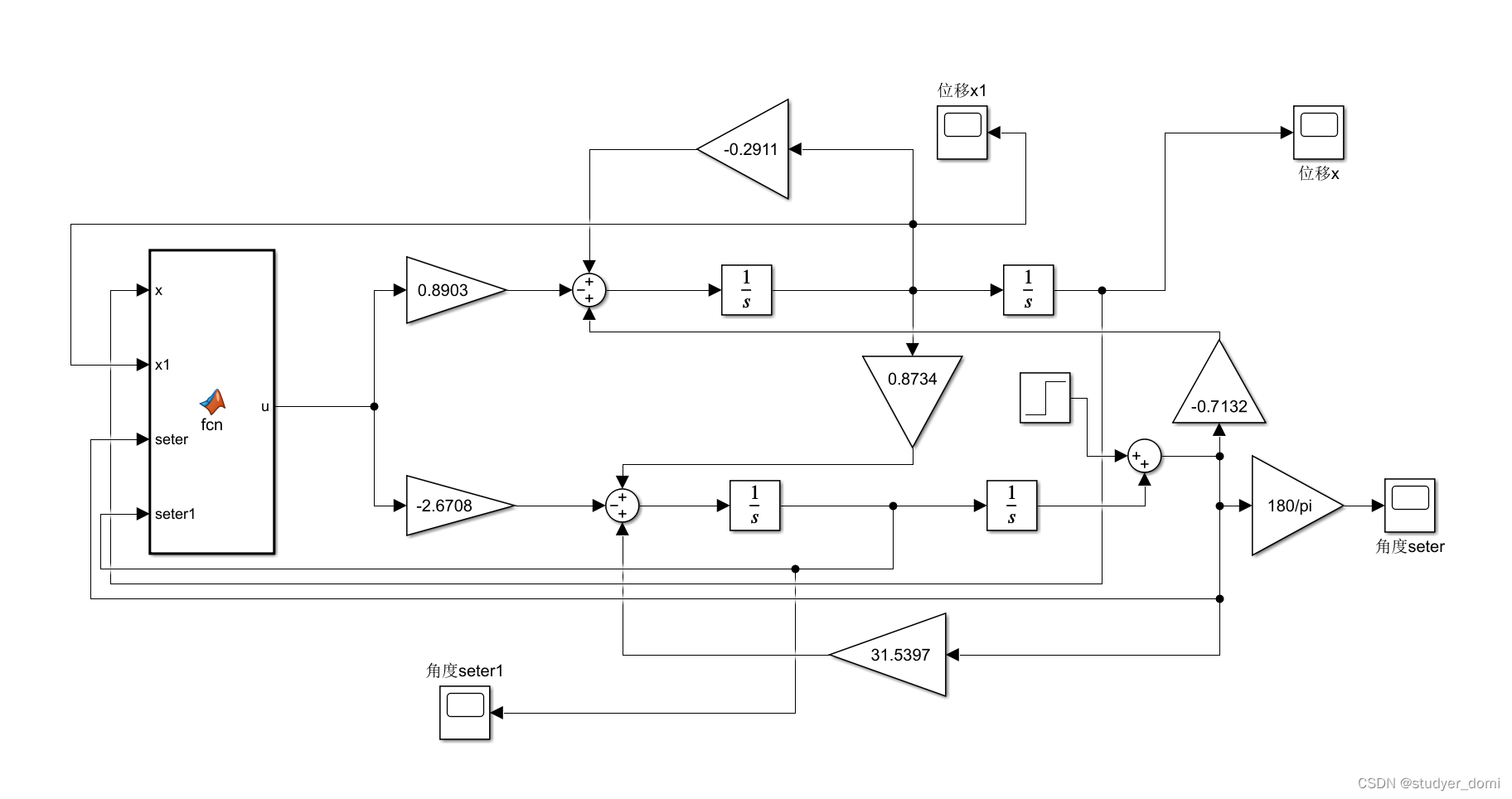
4、参考论文
略
