当前位置：首页 > article >正文

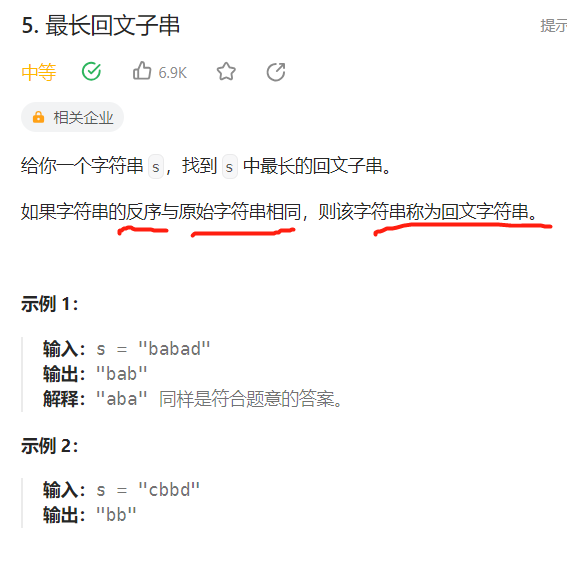
【LeetCode】5. 最长回文子串

article 2024/9/25 9:36:46

题目链接

文章目录

- Python3
- - 方法：暴力求解 $\lgroup O(n^3)、O(1)\rgroup$
  - 方法一：动态规划 (回文串同时去掉头尾后依然是回文串) $\lgroup O(n^2)\rgroup$
  - ⭐ 方法二：中心扩展法 $\lgroup O(n^2)、O(1)\rgroup$
  - ⭐ 方法三：Manacher(马拉车) 法 $\lgroup O(n)\rgroup$ 【空间换时间】
  - - - 写法一：维护盒子左右两边
      - 写法二：维护盒子右侧和中心
- C++
- - 方法二：中心扩展法 $\lgroup O(n^2)、O(1)\rgroup$
  - 方法三：Manacher(马拉车) 法 $\lgroup O(n)\rgroup$ 【空间换时间】
  - - 写法一：维护盒子左右两侧下标
    - 写法二：维护盒子中心下标和右侧下标
    - Manacher(马拉车) 法理解参考

Python3

方法：暴力求解 $\lgroup O(n^3)、O(1)\rgroup$

class Solution:
    def longestPalindrome(self, s: str) -> str:
        if s == s[::-1]:
            return s
        n = len(s)
        res = s[0]
        max_length = 1 # 至少一个字符
        for i in range(n-1): # 
            for j in range(i+1, n):
                if j - i + 1 > max_length and s[i:j+1] == s[i:j+1][::-1]: # s[i:i+1] 必然回文，直接跳过
                    res = s[i:j+1]
                    max_length = j - i + 1
                        

        return res

方法一：动态规划 (回文串同时去掉头尾后依然是回文串) $\lgroup O(n^2)\rgroup$

在这里插入图片描述

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if s == s[::-1] or n <= 1:
            return s
        
        dp = [[False]*n for _ in range(n)]
        for i in range(n):
            dp[i][i] = True
        
        max_length = 1
        index_left = 0  # 维护 前后界下标 占用的空间 似乎 比 直接维护 字符串少些

        for right in range(1, n):
            for left in range(right):
                if s[left] == s[right]:
                    if right - left <= 2: ##  aba(right-left==2)  aa(right-left==1)
                        dp[left][right] = True 
                    else:  # 长度 大于 3或2, 取决于 同时去掉两端的字符串 为回文
                        dp[left][right] = dp[left+1][right-1]
                
                ## 处理好后，判断
                if right - left + 1 > max_length and dp[left][right]: # 当长度 够长 才 决定是否更新
                    max_length = right - left + 1  # 注意长度计算
                    index_left = left 
                
        return s[index_left : index_left + max_length] # 注意 转换

在这里插入图片描述

⭐ 方法二：中心扩展法 $\lgroup O(n^2)、O(1)\rgroup$

class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 子模块 中心扩散
        def expandAroundCenter(s, left, right):
            while left >= 0 and right <= len(s)-1 and s[left] == s[right]:
                left -= 1
                right += 1

            return left+1, right-1  ## 返回 回文字符串 左右 下标    ab 01  


        # 主模块
        ## 处理特殊情况
        n = len(s)
        if s == s[::-1] or n <= 1:
            return s 
        
        max_length = 1
        index_left = 0
        for i in range(n):
            left1, right1 = expandAroundCenter(s, i, i)  ## 中心为一个字符
            left2, right2 = expandAroundCenter(s, i, i+1)  # 中心为 两个一样的字符
            if right1- left1 + 1 > max_length: 
                max_length = right1 - left1 + 1 
                index_left = left1 
            if right2 - left2 + 1 >  max_length:
                max_length = right2 - left2 + 1
                index_left  = left2  

        return s[index_left : index_left+max_length]

在这里插入图片描述

⭐ 方法三：Manacher(马拉车) 法 $\lgroup O(n)\rgroup$ 【空间换时间】

在这里插入图片描述

写法一：维护盒子左右两边

class Solution:
    #  子模块   中心扩散模块    盒外 以及 边界 仍需要扩展  
    def expandAroundCenter(self, s, left, right):
        while left >= 0 and right <= len(s)-1 and s[left] == s[right]:
            left -= 1
            right += 1

        ## 由于 边界是必定满足的，所以循环跳出 必定是 s[left] != s[right]
        # return s[left+1: right]  ### 注意 切片[] 是左合右开的
        return (right - left - 2) // 2  ## 注意这里要返回 回文半径 =[right - 1 - (left+1)] //2    
    # 主模块
    def longestPalindrome(self, s: str) -> str:
        """马拉车(统一处理奇偶回文串、进一步利用之前记录的对称关系)"""

        s = '#' + '#'.join(list(s)) + '#'  ## 插入特殊字符，s改造后 总长度为奇
        d = []   ## 记录 回文半径

        start, end = 0, -1   ## 用于 记录 最长回文串的起始和终止位置
        right = -1   ## 维护 盒子的 右端位置, 根据  回文串的特性， left = 2 * center - right
        left = 0   ## 维护盒子  左边 位置
        
        ## 写入 回文半径 d
        d.append(1)
        for i in range(1, len(s)):
            if i <= right: ## 位于 盒内 和边界
                mirror_left = left + right - i  ## 左边镜像的位置
                min_d = min(d[mirror_left], right-i)   ## 只扩展 盒子外的
                cur_d = self.expandAroundCenter(s, i - min_d, i + min_d)  ## 左右扩展
            else:
                cur_d = self.expandAroundCenter(s, i, i) ## 位于 盒外，无法利用之前的信息，直接左右扩展
            d.append(cur_d)

            if i + cur_d > right: ### 更新盒子 的左边界 和 右边界
                left =  i - cur_d 
                right = i + cur_d

            ## 更新  最长回文串的  位置
            if right - left > end - start:
                start = left
                end = right

        return s[start + 1 : end + 1 : 2]

写法二：维护盒子右侧和中心

class Solution:
    # 子模块
    def expandAroundCenter(self, s, left, right):
        while left >= 0 and right <= len(s)-1 and s[left] == s[right]:
            left -= 1
            right += 1

        return (right - left - 2) // 2  # 返回 回文半径

    # 主模块
    def longestPalindrome(self, s: str) -> str:
        # 改造 s ,统一成  奇数长度
        s = '#' + '#'.join(list(s)) + '#'

        d = []  # 记录回文半径

        start, end = 0, -1  ## 回文串 起始 和 结束 下标
        center = 0  # 盒子中心坐标
        right = -1 # 盒子 右侧下标

        d.append(1)
        for i in range(1, len(s)):
            if i <= right: 
                mirror_left = 2 * center - i
                min_d = min(d[mirror_left], right-i)
                cur_d = self.expandAroundCenter(s, i - min_d, i + min_d)
            else:
                cur_d = self.expandAroundCenter(s, i, i)
            d.append(cur_d)
            
            # 更新 盒子
            if i + cur_d > right:
                center = i 
                right = i + cur_d 

            # 更新 最长回文串 位置
            if 2 * cur_d + 1 > end - start:
                start = i - cur_d 
                end = i + cur_d 
        return s[start + 1 : end + 1 : 2]

在这里插入图片描述

C++

方法二：中心扩展法 $\lgroup O(n^2)、O(1)\rgroup$

class Solution {
public:
    // 子模块
    pair<int, int> expandAroundCenter(const string & s,int left, int right){
        while (left >= 0 && right <= s.size()-1 && s[left] == s[right]){
            --left;
            ++right;
        }
        return {left + 1, right - 1};
    }

    // 主模块
    string longestPalindrome(string s) {
        int start = 0, end = 0; // 当前 回文串 的起止下标
        for (int i = 0; i < s.size(); ++i){
            auto [left1, right1] = expandAroundCenter(s, i, i);
            auto [left2, right2] = expandAroundCenter(s, i, i+1);
            if (right1 - left1 > end - start){
                start = left1;
                end = right1;
            }
            if (right2 - left2 > end - start){
                start = left2;
                end = right2;
            }
        }
        return s.substr(start, end - start + 1);   // 注意写法
    }
};

方法三：Manacher(马拉车) 法 $\lgroup O(n)\rgroup$ 【空间换时间】

写法一：维护盒子左右两侧下标

class Solution {
public:
    // 子模块
    int expandAroundCenter(const string &s, int left, int right){
        while (left >= 0 && right <= s.size()-1 && s[left] == s[right]){
            --left;
            ++right;
        }
        return (right - left - 2)/2;  // 返回  回文半径
    }

    // 主模块
    string longestPalindrome(string s){
        // 修改s  插入特殊字符
        string t = "#";  // 注意是字符串 形式
        for (char c : s){
            t += c;
            t += '#';
        }
        t += '#';
        s = t;

        int start = 0, end = -1;  // 维护 最长回文串的 起止下标
        int left = 0, right = -1;
        vector<int> d; 
        d.emplace_back(1);
        for (int i = 1; i < s.size(); ++i){
            int cur_d;
            if (i <= right){// 位于盒内 或 边界
                int mirror_left = left + right - i;
                int min_d = min(d[mirror_left], right - i);
                cur_d = expandAroundCenter(s, i - min_d, i + min_d);
            }
            else{
                cur_d = expandAroundCenter(s, i, i);  //奇数情况
            }
            d.emplace_back(cur_d);

            if (i + cur_d > right){
                left = i - cur_d;
                right = i + cur_d;
            }
            
            if (right - left > end - start){
                start = left;
                end = right;
            }
        }
        string res;
        for (int i = start; i <= end; ++i){
            if (s[i] != '#'){
              res += s[i];  
            }
        }
        return res;
    }
};

写法二：维护盒子中心下标和右侧下标

class Solution {
public:
    // 子模块
    int expandAroundCenter(const string &s, int left, int right){
        while (left >= 0 and right <= s.size() - 1 && s[left] == s[right]){
            --left;
            ++right;
        }
        return (right - left - 2)/2; // 返回 回文半径
    }

    // 主模块
    string longestPalindrome(string s) {
        // 修改 s   统一成 奇长度
        string t = "#";
        for (char c : s){
            t += c;
            t += '#';
        }
        t += '#';
        s = t;

        // 存储 回文半径
        vector<int> d;
        d.emplace_back(1);
        int start = 0, end = -1; // 最长 回文串 的起止下标
        int center = 0, right = -1;  // 盒子 的 中间下标 和 右侧下标
        for (int i = 1; i < s.size(); ++i){
            int cur_d;
            if (i <= right){
                int mirror_left = 2 * center - i;
                int min_d = min(d[mirror_left], right-i);
                cur_d = expandAroundCenter(s, i - min_d, i + min_d);
            }
            else{
                cur_d = expandAroundCenter(s, i, i);   // 盒子外， 中心扩展
            }
            d.emplace_back(cur_d);

            if (i + cur_d > right){
                center = i;
                right = i + cur_d;
            }

            // 更新 最长 回文串 的起止下标
            if (2 * cur_d + 1 > end - start){
                start = i - cur_d;
                end = i + cur_d;
            }
        }
        string res;
        for (int i = start; i <= end; ++i){ // 注意 起止
            if (s[i] != '#'){
                res += s[i];
            }
        }
        return res;
    }
};