吴恩达《机器学习》2-5->2-7:梯度下降算法与理解
一、梯度下降算法
梯度下降算法的目标是通过反复迭代来更新模型参数,以便最小化代价函数。代价函数通常用于衡量模型的性能,我们希望找到使代价函数最小的参数值。这个过程通常分为以下几个步骤:
-
初始化参数: 随机或设定初始参数的数值,如 𝜃0, 𝜃1, ..., 𝜃𝑛。
-
计算代价函数的梯度: 对于每个参数 𝜃𝑗,计算代价函数 J(𝜃0, 𝜃1, ..., 𝜃𝑛) 对该参数的偏导数,即梯度,表示为 ∂J/∂𝜃𝑗。
-
更新参数: 使用梯度信息来更新参数,根据以下规则更新每个参数 𝜃𝑗
𝜃𝑗 := 𝜃𝑗 - 𝛼 * ∂J/∂𝜃𝑗 其中,𝛼是学习率(learning rate),它决定了每次参数更新的步长。 -
重复迭代: 重复步骤2和步骤3,直到满足停止条件,如达到最大迭代次数或梯度足够小。
二、批量梯度下降
批量梯度下降(Batch Gradient Descent)是一种梯度下降的变体,其中在每一次参数更新时,使用整个训练数据集的信息。更新规则如下:
Repeat {
𝜃𝑗 := 𝜃𝑗 - 𝛼 * (1/𝑚) * ∑ (ℎ𝜃(𝑥(𝑖)) - 𝑦(𝑖)) * 𝑥(𝑖) for 𝑖 = 1 to 𝑚
}
这表示在每一次迭代中,我们计算所有训练样本的梯度,然后对所有参数进行同时更新。

三、学习率的选择
学习率 𝛼 是一个重要的超参数,它控制了参数更新的速度。如果 𝛼 太小,模型会收敛得很慢,需要更多的迭代次数才能达到最小值。如果 𝛼 太大,可能会导致无法收敛,甚至发散。
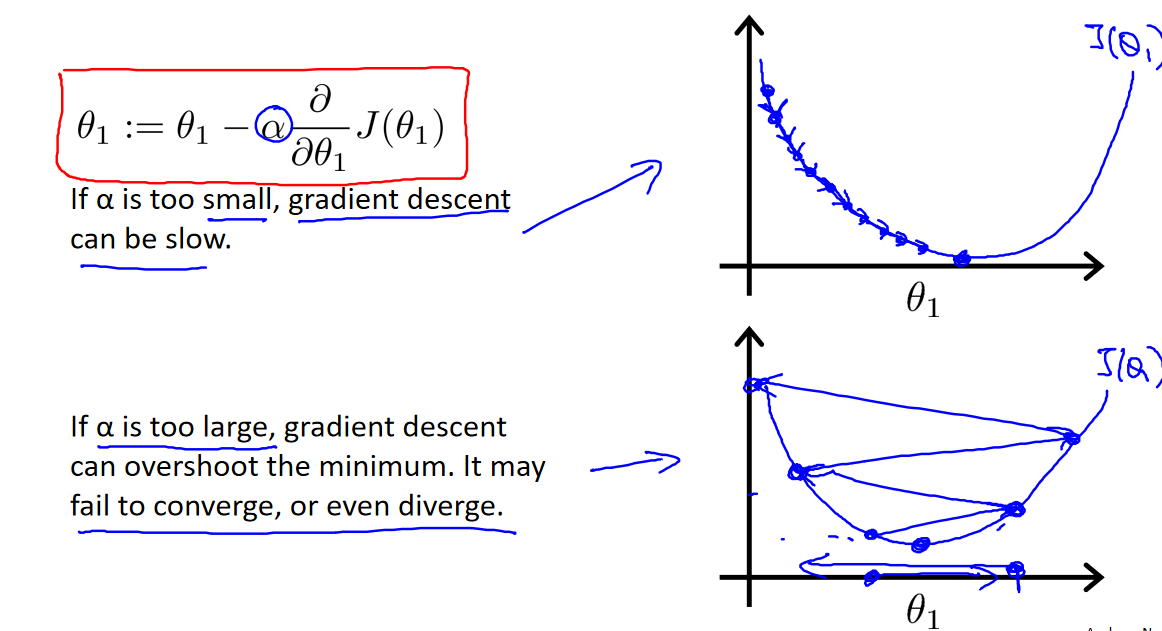
在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的幅度,这是因为当我们接近局部最低点时,很显然在局部最低时导数等于零,所以当我们接近局部最低时,导数值会自动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小𝑎。
四、局部最小值
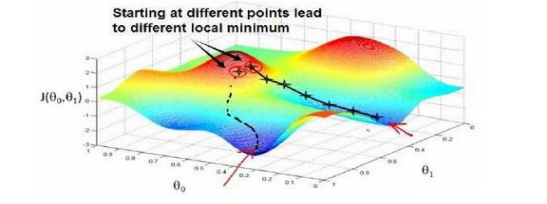
梯度下降通常会找到一个局部最小值,因为它不会尝试所有可能的参数组合。选择不同的初始参数组合可能导致不同的局部最小值。全局最小值通常很难找到,特别是对于复杂的代价函数。
参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记
