当前位置： 首页 > article >正文

【数据结构】Map和Set

article 2024/11/15 2:06:51

⭐ 作者：小胡_不糊涂
🌱 作者主页：小胡_不糊涂的个人主页
📀 收录专栏：浅谈数据结构
💖 持续更文，关注博主少走弯路，谢谢大家支持 💖

Map、Set

  • 1. 搜索树
    • 1.1 概念
    • 1.2 性能分析
  • 2. 搜索
    • 2.1 概念及场景
    • 2.2 模型
  • 3. Map的使用
    • 3.1 关于Map.Entry<K, V>的说明
    • 3.2 Map的常用方法说明
    • 3.4 TreeMap的使用案例
  • 4. Set的说明
    • 4.1 常见方法说明
    • 4.2 TreeSet的使用案例

在这里插入图片描述

1. 搜索树

1.1 概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

下图就是一个二叉搜索树：

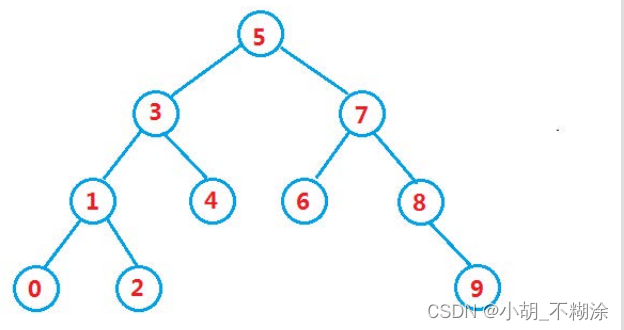
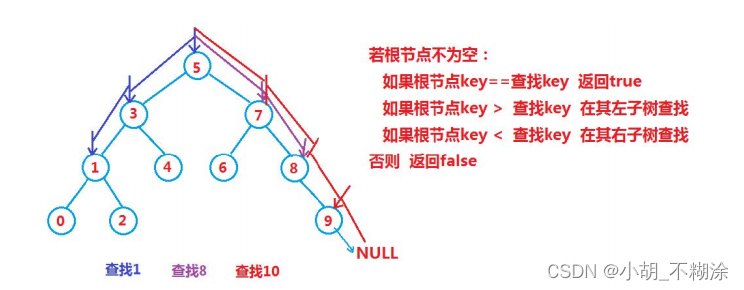
在这里插入图片描述

进行查找操作：
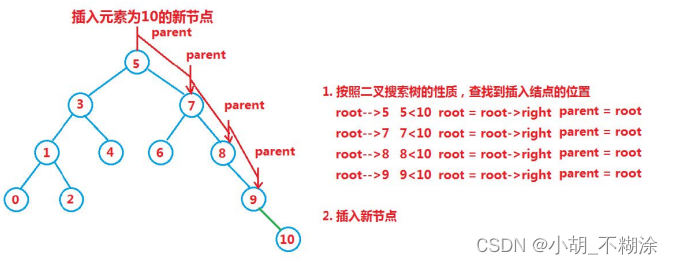
在这里插入图片描述

进行插入操作：
1. 树为空树
在这里插入图片描述
2. 如果树不是空树，按照查找逻辑确定插入位置，插入新结点
在这里插入图片描述
进行删除操作：
设待删除结点为 cur, 待删除结点的双亲结点为 parent

  1. cur.left == null
    cur 是 root，则 root = cur.right
    cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
    cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
  2. cur.right == null
    cur 是 root，则 root = cur.left
    cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
    cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
  3. cur.left != null && cur.right != null
    需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

在这里插入图片描述
代码实现：

public class BinarySearchTree {
    public static class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        public TreeNode(int val){
            this.val=val;
        }
    }
    public TreeNode root;

    /**
     * 查找元素
     * 最好情况：完全二叉树 O(logN)
     * 最坏情况: 单分支的树 O(N)
     * @param key
     * @return
     */
    public boolean search(int key){
        TreeNode cur=root;
        while(cur!=null){
            if(cur.val==key){
                return true;
            }else if(cur.val>key){
                cur=cur.left;
            }else{
                cur=cur.right;
            }
        }
        return false;
    }

    //插入元素
    public boolean insert(int key){
        if(root==null){
            root=new TreeNode(key);
            return true;
        }
        TreeNode cur=root;
        TreeNode parent=null;
        while(cur!=null){
            if(cur.val>key){
                parent=cur;
                cur=cur.left;
            }else if(cur.val<key){
                parent=cur;
                cur=cur.right;
            }else{
                return false;//树中不能有相等元素
            }
        }
        //若cur=null，判断key与父亲节点的大小
        if(parent.val>key){
            parent.left=new TreeNode(key);
        }
        if(parent.val<key){
            parent.right=new TreeNode(key);
        }
        return true;
    }

	//删除元素
    public void remove(int key){
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null) {
            if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else if(cur.val > key) {
                parent = cur;
                cur = cur.left;
            }else {
                //开始删除
                removeNode(cur,parent);
            }
        }
    }
    public void removeNode(TreeNode cur,TreeNode parent){
        //第一种情况
        if(cur.left==null){
            if(cur==root){
                root=cur.right;
            }
            if(cur==parent.left){
                parent.left=cur.right;
            }
            if(cur==parent.right){
                parent.right=cur.right;
            }
        }
        //第二种情况
        if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }
        //第三种情况
        if(cur.left!=null && cur.right!=null){
            TreeNode targetParent = cur;
            TreeNode target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            //删除target
            if(targetParent.left == target) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
}

1.2 性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。

但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
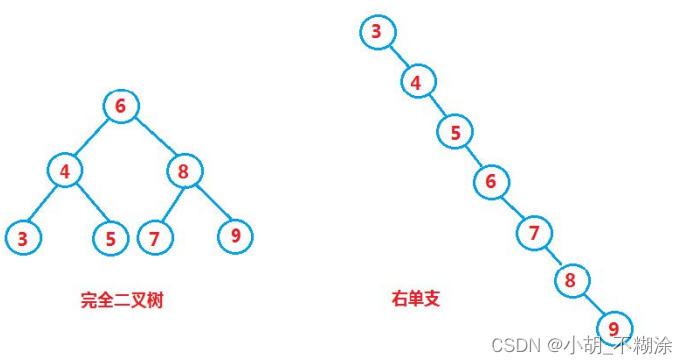
在这里插入图片描述

最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：log2(N)
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：N/2

2. 搜索

2.1 概念及场景

Map 和 Set 是一种专门用来进行搜索的容器或者数据结构，其搜索的效率与其具体的实例化子类有关。 以前常见的搜索方式有：

  1. 直接遍历，时间复杂度为O(N)，元素如果比较多效率会非常慢
  2. 二分查找，时间复杂度为，但搜索前必须要求序列是有序的

上述排序比较适合静态类型的查找，即一般不会对区间进行插入和删除操作了，而现实中的查找比如：

  1. 根据姓名查询考试成绩
  2. 通讯录，即根据姓名查询联系方式
  3. 不重复集合，即需要先搜索关键字是否已经在集合中
    可能在查找时进行一些插入和删除，即动态查找，那上述两种方式就不太适合了，而 Map 和 Set 则是一种适合动态查找的集合容器。

2.2 模型

一般把搜索的数据称为关键字（Key），和关键字对应的称为值（Value），将其称之为Key-value的键值对，所以模型会有两种：

  1. 纯 key 模型，比如：
  • 有一个英文词典，快速查找一个单词是否在词典中
  • 快速查找某个名字在不在通讯录中
  1. Key-Value 模型，比如：
  • 统计文件中每个单词出现的次数，统计结果是每个单词都有与其对应的次数：<单词，单词出现的次数>
    而Map中存储的就是key-value的键值对，Set中只存储了Key

3. Map的使用

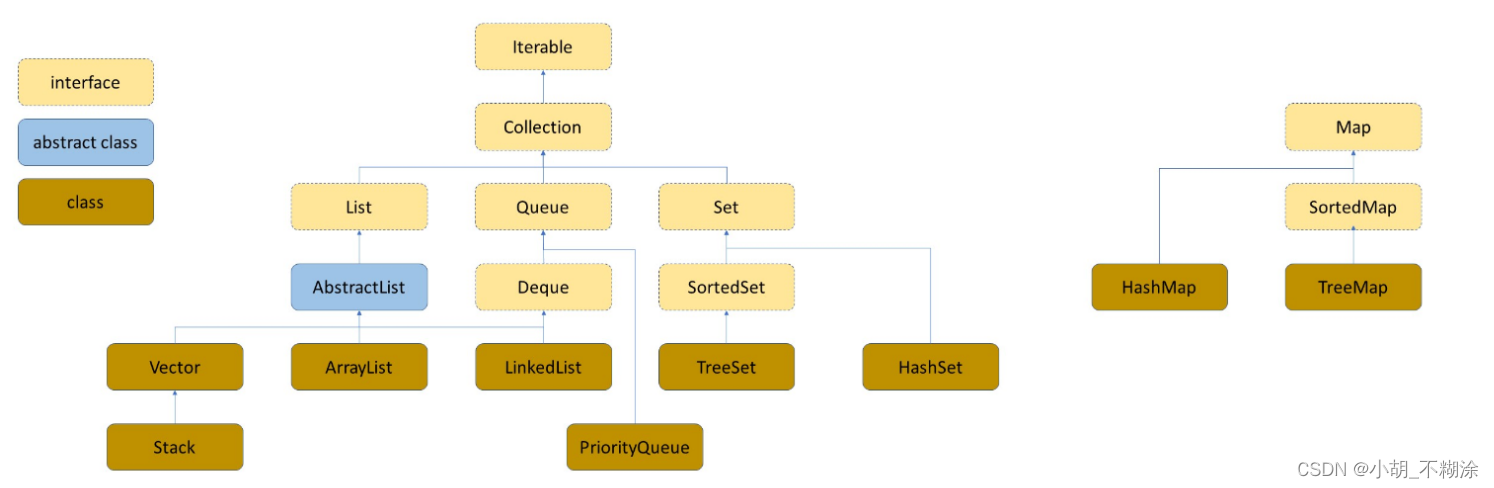
在这里插入图片描述
在这里插入图片描述
Map是一个接口类，该类没有继承自Collection，该类中存储的是<K,V>结构的键值对，并且K一定是唯一的，不能重复。

3.1 关于Map.Entry<K, V>的说明

Map.Entry<K, V> 是Map内部实现的用来存放<key, value>键值对映射关系的内部类，该内部类中主要提供了<key, value>的获取，value的设置以及Key的比较方式。

方法解释
K getKey()返回 entry 中的 key
V getValue()返回 entry 中的 value
V setValue(V value)将键值对中的value替换为指定value

Map.Entry<K,V>并没有提供设置Key的方法

3.2 Map的常用方法说明

方法解释
V get(Object key)返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)返回 key 对应的 value，key 不存在，返回默认值
V put(K key, V value)设置 key 对应的 value
V remove(Object key)删除 key 对应的映射关系
Set keySet()返回所有 key 的不重复集合
Collection values()返回所有 value 的可重复集合
Set<Map.Entry<K, V>> entrySet()返回所有的 key-value 映射关系
boolean containsKey(Object key)判断是否包含 key
boolean containsValue(Object value)判断是否包含 value

注：

  1. Map是一个接口，不能直接实例化对象，如果要实例化对象只能实例化其实现类TreeMap或者HashMap
  2. Map中存放键值对的Key是唯一的，value是可以重复的
  3. 在TreeMap中插入键值对时，key不能为空，否则就会抛NullPointerException异常，value可以为空。但是HashMap的key和value都可以为空。
  4. Map中的Key可以全部分离出来，存储到Set中来进行访问(因为Key不能重复)。
  5. Map中的value可以全部分离出来，存储在Collection的任何一个子集合中(value可能有重复)。
  6. Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉，然后再来进行重新插入。
  7. TreeMap和HashMap的区别：
Map底层结构TreeMapHashMap
底层结构红黑树哈希桶
插入/删除/查找时间复杂度O(log2(N))O(1)
是否有序关于Key有序无序
线程安全不安全不安全
插入/删除/查找区别需要进行元素比较通过哈希函数计算哈希地址
比较与覆写key必须能够比较，否则会抛出ClassCastException异常自定义类型需要覆写equals和hashCode方法
应用场景需要Key有序场景下Key是否有序不关心，需要更高的时间性能

3.4 TreeMap的使用案例

public static void TestMap(){
        Map<String, String> m = new TreeMap<>();
        // put(key, value):插入key-value的键值对
        // 如果key不存在，会将key-value的键值对插入到map中,返回null
        m.put("林冲", "豹子头");
        m.put("鲁智深", "花和尚");
        m.put("武松", "行者");
        m.put("宋江", "及时雨");
        String str = m.put("李逵", "黑旋风");
        System.out.println(m.size());//5
        System.out.println(m);
        //{宋江=及时雨, 李逵=黑旋风, 林冲=豹子头, 武松=行者, 鲁智深=花和尚}

        // put(key,value): 注意key不能为空，但是value可以为空
        // key如果为空，会抛出空指针异常
        //m.put(null, "花名");
        str = m.put("无名", null);
        System.out.println(m.size());//6

        // put(key, value):
        // 如果key存在，会使用value替换原来key所对应的value，返回旧value
        str = m.put("李逵", "铁牛");

        // get(key): 返回key所对应的value
        // 如果key存在，返回key所对应的value
        // 如果key不存在，返回null
        System.out.println(m.get("鲁智深"));//花和尚
        System.out.println(m.get("史进"));//null

        //GetOrDefault(): 如果key存在，返回与key所对应的value，如果key不存在，返回一个默认值
        System.out.println(m.getOrDefault("李逵", "铁牛"));//铁牛
        System.out.println(m.getOrDefault("史进", "九纹龙"));//九纹龙
        System.out.println(m.size());//6

        //containKey(key)：检测key是否包含在Map中，时间复杂度：O(logN)
        // 按照红黑树的性质来进行查找
        // 找到返回true，否则返回false
        System.out.println(m.containsKey("林冲"));//true
        System.out.println(m.containsKey("史进"));//false
        
        // containValue(value): 检测value是否包含在Map中，时间复杂度: O(N)
        // 找到返回true，否则返回false
        System.out.println(m.containsValue("豹子头"));//true
        System.out.println(m.containsValue("九纹龙"));//false
        
        // 打印所有的key
        // keySet是将map中的key防止在Set中返回的
        for(String s : m.keySet()){
            System.out.print(s + " ");//宋江 无名 李逵 林冲 武松 鲁智深 
        }
        System.out.println();
        
        // 打印所有的value
        // values()是将map中的value放在collect的一个集合中返回的
        for(String s : m.values()){
            System.out.print(s + " ");//及时雨 null 铁牛 豹子头 行者 花和尚
        }
        System.out.println();
        
        // 打印所有的键值对
        // entrySet(): 将Map中的键值对放在Set中返回了
        for(Map.Entry<String, String> entry : m.entrySet()){
            System.out.println(entry.getKey() + "--->" + entry.getValue());
        }
        System.out.println();
        //宋江--->及时雨
        //无名--->null
        //李逵--->铁牛
        //林冲--->豹子头
        //武松--->行者
        //鲁智深--->花和尚
    }

4. Set的说明

Set与Map主要的不同有两点：Set是继承自Collection的接口类，Set中只存储了Key。

4.1 常见方法说明

方法解释
boolean add(E e)添加元素，但重复元素不会被添加成功
void clear()清空集合
boolean contains(Object o)判断 o 是否在集合中
Iterator iterator()返回迭代器
boolean remove(Object o)删除集合中的 o
int size()返回set中元素的个数
boolean isEmpty()检测set是否为空，空返回true，否则返回false
Object[] toArray()将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)集合c中的元素是否在set中全部存在，是返回true，否则返回false
boolean addAll(Collection<? extendsE> c)将集合c中的元素添加到set中，可以达到去重的效果

注意：

  1. Set是继承自Collection的一个接口类
  2. Set中只存储了key，并且要求key一定要唯一
  3. TreeSet的底层是使用Map来实现的，其使用key与Object的一个默认对象作为键值对插入到Map中的
  4. Set最大的功能就是对集合中的元素进行去重
  5. 实现Set接口的常用类有TreeSet和HashSet，还有一个LinkedHashSet，LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
  6. Set中的**Key不能修改，**如果要修改，先将原来的删除掉，然后再重新插入
  7. TreeSet中不能插入null的key，HashSet可以。
  8. TreeSet和HashSet的区别：
Set底层结构TreeSetHashSet
底层结构红黑树哈希桶
插入/删除/查找时间复杂度O(log2(N)O(1)
是否有序关于Key有序不一定有序
线程安全不安全不安全
插入/删除/查找区别按照红黑树的特性来进行插入和删除1. 先计算key哈希地址 2. 然后进行
插入和删除
比较与覆写key必须能够比较，否则会抛出ClassCastException异常自定义类型需要覆写equals和hashCode方法
应用场景需要Key有序场景Key是否有序不关心，需要更高的时间性能

4.2 TreeSet的使用案例

public static void TestSet(){
        Set<String> s = new TreeSet<>();
        // add(key): 如果key不存在，则插入，返回ture
        // 如果key存在，返回false
        boolean isIn = s.add("apple");
        s.add("orange");
        s.add("peach");
        s.add("banana");
        System.out.println(s.size());//4
        System.out.println(s);//[apple, banana, orange, peach]
        isIn = s.add("apple");
        
        // add(key): key如果是空，抛出空指针异常
        //s.add(null);
        // contains(key): 如果key存在，返回true，否则返回false
        System.out.println(s.contains("apple"));//true
        System.out.println(s.contains("watermelen"));//false
        
        // remove(key): key存在，删除成功返回true
        // key不存在，删除失败返回false
        // key为空，抛出空指针异常
        s.remove("apple");
        System.out.println(s);//[banana, orange, peach]
        s.remove("watermelen");
        System.out.println(s);//[banana, orange, peach]
        
        Iterator<String> it = s.iterator();
        while(it.hasNext()){
            System.out.print(it.next() + " ");
        }
        System.out.println();
        //banana orange peach
    }

http://www.kler.cn/a/108682.html

相关文章：

  • Python中异常处理小测验
  • 【OceanBase 诊断调优】—— ocp上针对OB租户CPU消耗计算逻辑
  • jmeter常用配置元件介绍总结之后置处理器
  • 什么是RAG? LangChain的RAG实践！
  • Python标准库模块的使用：math、datetime
  • c#使用COM接口设置excel单元格宽高匹配图片，如何计算？
  • 深入浅出排序算法之基数排序
  • OS的Alarm定时器调度机制
  • oracle，CLOB转XML内存不足，ORA-27163: out of memory ORA-06512: at “SYS.XMLTYPE“,
  • Think-Queue3一直提示[Exception]redis扩展未安装
  • 开源B2B网站电子商务平台源码下载搭建 实现高效交易的桥梁
  • Kotlin数据流概览
  • server2012 通过防火墙开启局域网内限定IP进行远程桌面连接
  • 工作组与域
  • 基于SSM的汽车维修管理系统
  • 透明安全地解释Moonbeam基金会分配的GLMR去了哪
  • 【K8S】常用的 Kubernetes（K8S）指令
  • LV.12 D12 GPIO实验 学习笔记
  • Makefile泛谈
  • 9、电路综合-基于简化实频的任意幅频响应的微带电路设计
  • 【zookeeper】zk的ZAB原子广播协议
  • C语言实现输入一个字符串，递归将其逆序输出
  • appium操控微信小程序的坑
  • 【iOS】——知乎日报第二周总结
  • 【Java】Map集合中常用方法
  • 【2023年NCST C语言新生培训】| 五次培训总结 | C到C++内容补充 | 排位赛详细题解 |《万字长文》