当前位置：首页 > article >正文

【无功优化】基于多目标差分进化算法的含DG配电网无功优化模型【IEEE33节点】（Matlab代码实现）

article 2024/11/13 8:03:58

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章讲解

💥1 概述

多目标无功优化可在目标函数中兼顾经济性和电压稳定性，引起了研究人员的广泛关注。与单目标无功优化问题的本质区别在于，多目标无功优化的解不是唯一的，即不存在使经济性和电压

稳定性同时达到最优的解，而是存在一个非劣解的集合，称为帕累托(Pareto)最优集，集合中的元素就所有目标而言是不可比较的。当前多目标无功优化问题的求解方法大致可分为以下 2类：

1)先验法。通过事先设置反映各目标偏好程度的参数将多目标无功优化模型转化成单目标优

化问题进行求解，常用的方法有线性加权法[11-12]和模糊集理论[13-14]。这类方法虽然便于计算，但存在明显的缺点：权重向量或隶属度函数难以确定；每次计算只能得到一个控制方案，若要得到一组近似的 Pareto最优解，则需进行多次计算；对 Pareto前沿的形状敏感，若问题的 Pareto前沿是非凸集，则很难搜索到完整的 Pareto最优集。

2)后验法。该方法的特点是无需事先给出目标函数之间的优先关系，运行人员只需从 Pareto最

优集中选择出满足要求的控制方案。因此快速地获取具有良好分布且范围宽广的 Pareto前沿成为关键。文献 [15．16]分别应用强度 Pareto 进化算法 (strengthParetoevolutionaryalgorithm，SPEA)及其改进版本 SPEA2来求得 Pareto最优集；文献提出采用 NSGA—II来获取 Pareto前沿；另外以 PSO为框架的多目标优化技术也被用来求解多目标无功优化问题。然而上述算法常存在易陷入局部最优、非劣解分布不均匀、控制参数难以选择等缺陷。

多目标差分优化算法见第4部分。

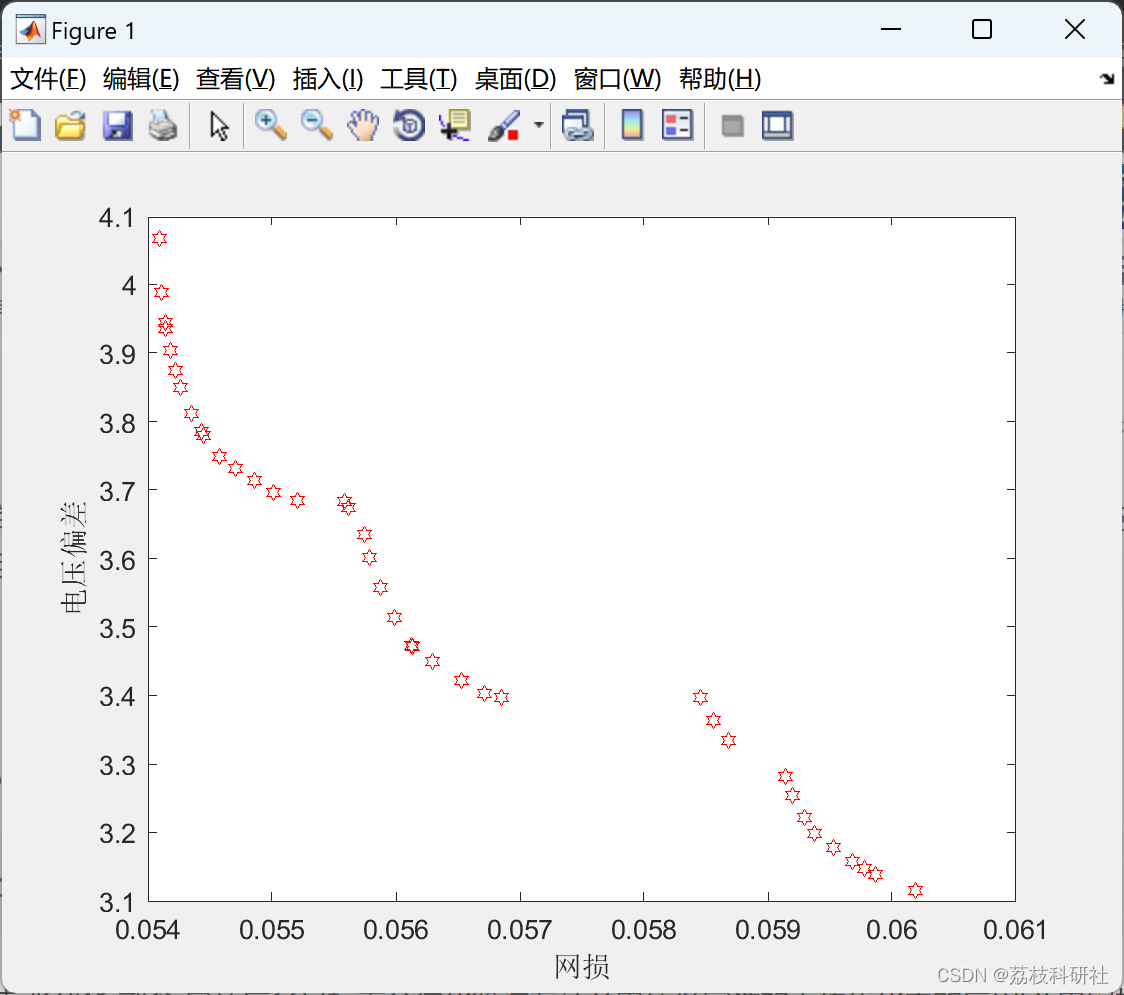
📚2 运行结果

图1为改进的IEEE33节点配电系统,在保持线路参数不变的前提下，增加﹖组并联补偿电容器和2个分布式电源。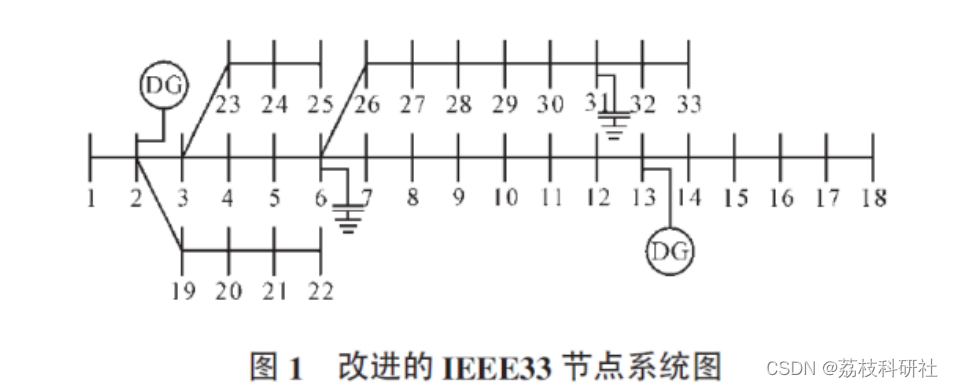

假定每个分布式电源能发出1MW的有功功率，且这②个分布式电源无功出力在-100~500 kvar区间内而且可调节;并联补偿电容器的补偿容量定为150 kvarx4和150 kvar×7。

部分代码：

% data=[1   2   0.0922   0.047   100   60   0
% 2   3   0.493   0.2511   (90-1000)   40   0
% 3   4   0.366   0.1864   120   80   0
% 4   5   0.3811   0.1941   60   30   0
% 5   6   0.819   0.707   60   20   0
% 6   7   0.1872   0.6188   200   (100-0*150)   0
% 7   8   0.7114   0.2351   200   100   0
% 8   9   1.03   0.74   60   20   0
% 9   10   1.044   0.74   60   20   0
% 10   11   0.1966   0.065   45   30   0
% 11   12   0.3744   0.1238   60   35   0
% 12   13   1.468   1.155   60   35   0
% 13   14   0.5416   0.7129   120   80   0
% 14   15   0.591   0.526   60   10   0
% 15   16   0.7463   0.545   60   20   0
% 16   17   1.289   1.721   60   20   0
% 17   18   0.372   0.574   90   40   0
% 2   19   0.164   0.1565   90   40   0
% 19   20   1.5042   1.3554   90   40   0
% 20   21   0.4095   0.4784   90   40   0
% 21   22   0.7089   0.9373   90   40   0
% 3   23   0.4512   0.3083   90   50   0
% 23   24   0.898   0.7091   420   200   0
% 24   25   0.896   0.7011   420   200   0
% 6   26   0.203   0.1034   60   25   0
% 26   27   0.2842   0.1447   60   25   0
% 27   28   1.059   0.9337   60   20   0
% 28   29   0.8042   0.7006   120   70   0
% 29   30   0.5075   0.2585   200   600   0
% 30   31   0.9744   0.963   150   70   0
% 31   32   0.3105   0.3619   210   (100-0*150)   0
% 32   33   0.341   0.5362   60   40   0
% 8   21   2   2   0   0   0
% 9   15   2   2   0   0   0
% 12   22   2   2   0   0   0
% 18   33   0.5   0.5   0   0   0
% 25   29   0.5   0.5   0   0   0
% ];

Y=1./Z;
Y00=zeros(1,33);
Sload=zeros(1,33);%各个母线负荷
for j=1:32
Sload(data(j,2))=data(j,5)+data(j,6)*i;
end
Sload=Sload/1000;
PQDGnun=0;
PVnun=0;
PQVDGnun=0;
PQVDGposition=[31];
PQVrePower=[0.5];
PQVmaxmin=[0.5;0];
PVposition=[22];%PV节点的位置
PVrePower=[0.5];
PVmaxmin=[0.5;0];%PV节点无功上下限
PVreacPower=[0.25]; %PV节点无功补偿的初始无功功率
PQDGposition=[7];
PQDGpower=[0.5+0.5i];
U=zeros(1,33)+10;%设置节点的电压初值
U(1)=12.66;
if PQVDGnun>0
for j=1:PQVDGnun
PQVreacPower(j)=-U(PQVDGposition(j))*U(PQVDGposition(j))/38+(-U(PQVDGposition(j))*U(PQVDGposition(j))+sqrt(U(PQVDGposition(j))^4-4*real(PQVrePower(j))*real(PQVrePower(j))*1.95*1.95))/(2*1.95);
end
else
PQVreacPower=0.5;%0.5没有任何意义，在后面也没有用到这个数字
end