【数据结构】图的存储结构及实现(邻接表和十字链表)
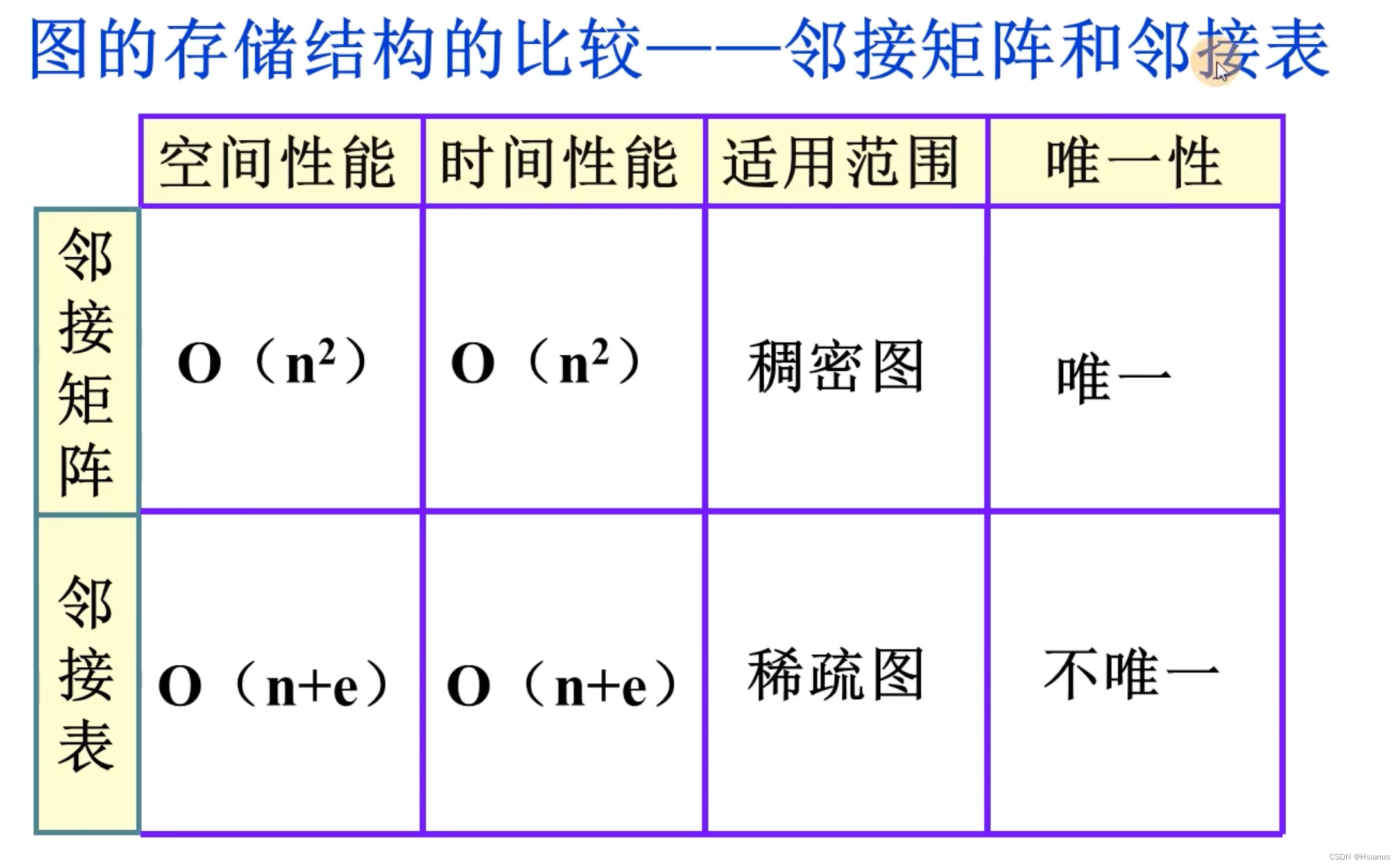
一.邻接矩阵的空间复杂度
假设图G有n个顶点e条边,则存储该图需要O(n^2)
不适用稀疏图的存储
二.邻接表
1.邻接表的存储思想:
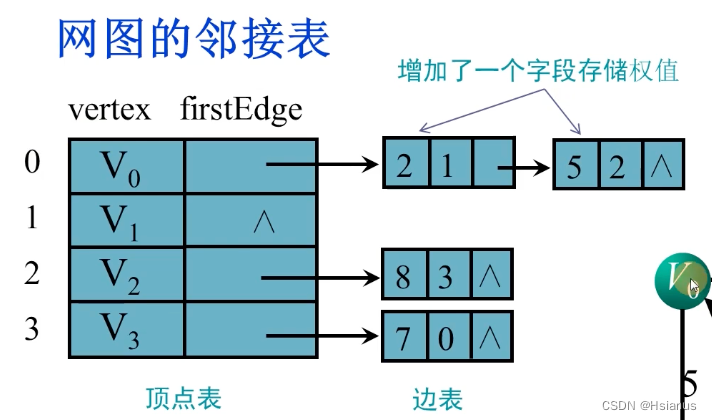
对于图的每个顶点vi,将所有邻接于vi的顶点链成一个单链表,称为顶点vi的边表(对于有向图则称为出边表),所有边表的头指针和存储顶点信息的一维数组构成了顶点表。
2.邻接表的结构定义
struct ArcNode{
int adjvex;
struct ArcNode *next;
};
template <class T>
struct VertexNode{
T vertex;
struct ArcNode *firstEdge;
};
邻接表的空间复杂度为O(n+e)
更适用于有向图的存储
3.无向图的邻接表
1.如何求顶点i的度?
顶点i的边表中结点的个数
2.如何判断顶点vi和vj之间是否有边?
测试顶点vi的边表中是否有终点为j的结点
4.有向图的邻接表
1.如何求顶点i的出度?
顶点i的边表中结点的个数
2.如何求顶点i的入度?
各顶点的出边表中以顶点i为终点的结点个数
5.网图的邻接表
三.邻接表存储有向图的类
struct ArcNode{
int adjvex;
struct ArcNode *next;
};
template <class T>
struct VertexNode{
T vertex;
struct ArcNode *firstEdge;
};
template <class T>
class ALGraph{
private:
VertexNode<T> adjList[MAX_VERTEX];
int vertexNum,arcNum;
public:
ALGraph(T v[],int n,int e);
~ALGraph();
void DFSTraverse();
void BFSTraverse();
};template <class T>
ALGraph<T>::ALGraph(T v[],int n,int e){
int vi,vj;
ArcNode *s;
vertexNum=n;
arcNum=e;
for(int i=0;i<n;i++){
adjList[i].vertex=v[i];
adjList[i].firstEdge=NULL;
}
for(int i=0;i<arcNum;i++){
cin>>vi>>vj;
s=new ArcNode;
s->adjvex=vj;
s->next=adjList[vi].firstEdge;
adjList[vi].firstEdge=s;
}
}
template <class T>
ALGraph<T>::~ALGraph(){
int i,j;
ArcNode *p;
for(i=0;i<vertexNum;i++){
p=adjList[i].firstEdge;
if(p){
while(p){
adjList[i].firstEdge=p->next;
delete p;
p=adjList[i].firstEdge;
}
}
}
}
四.逆邻接表
对于邻接表来说,查找入度非常困难。
所以引入了逆邻接表。
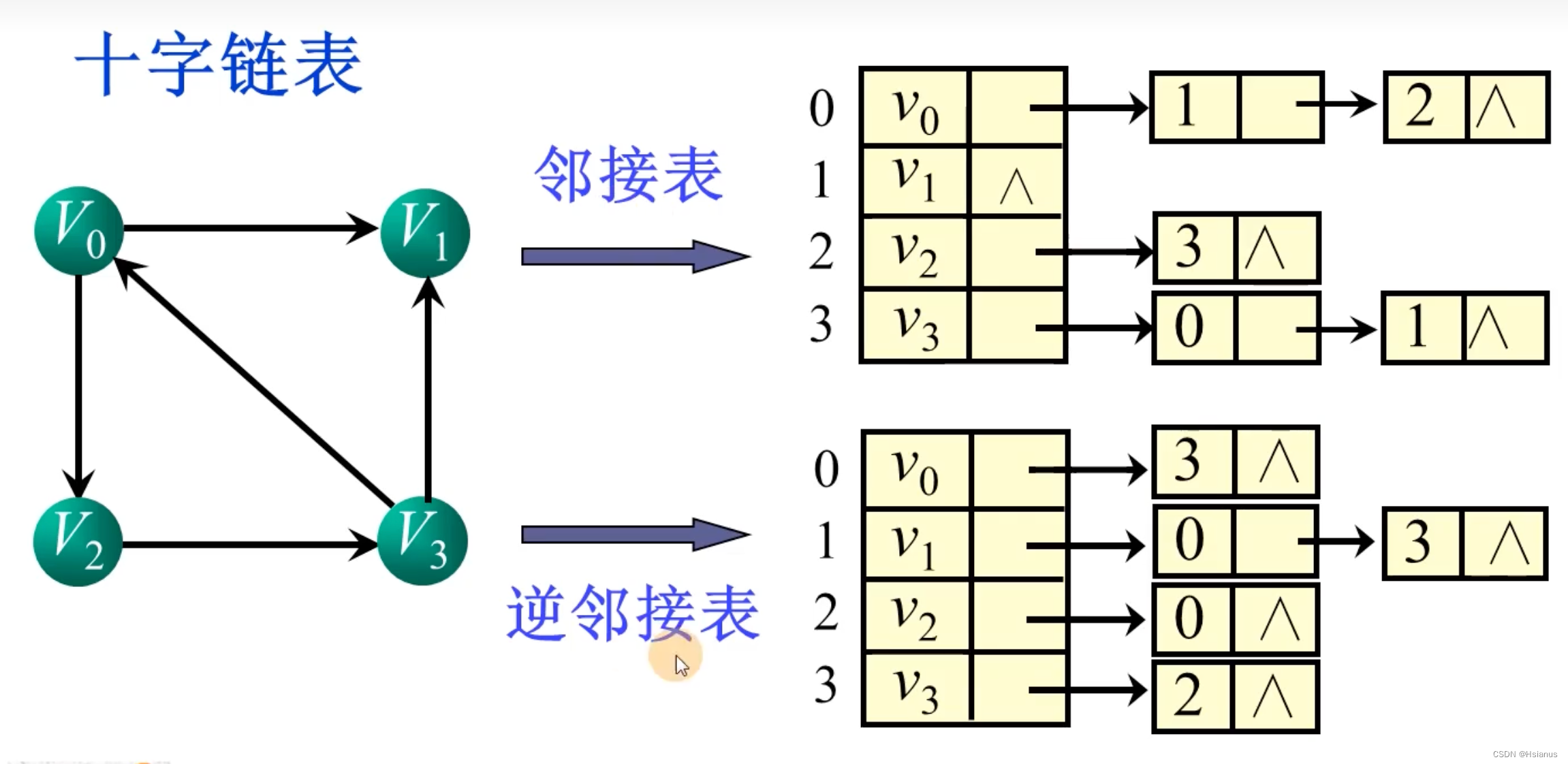
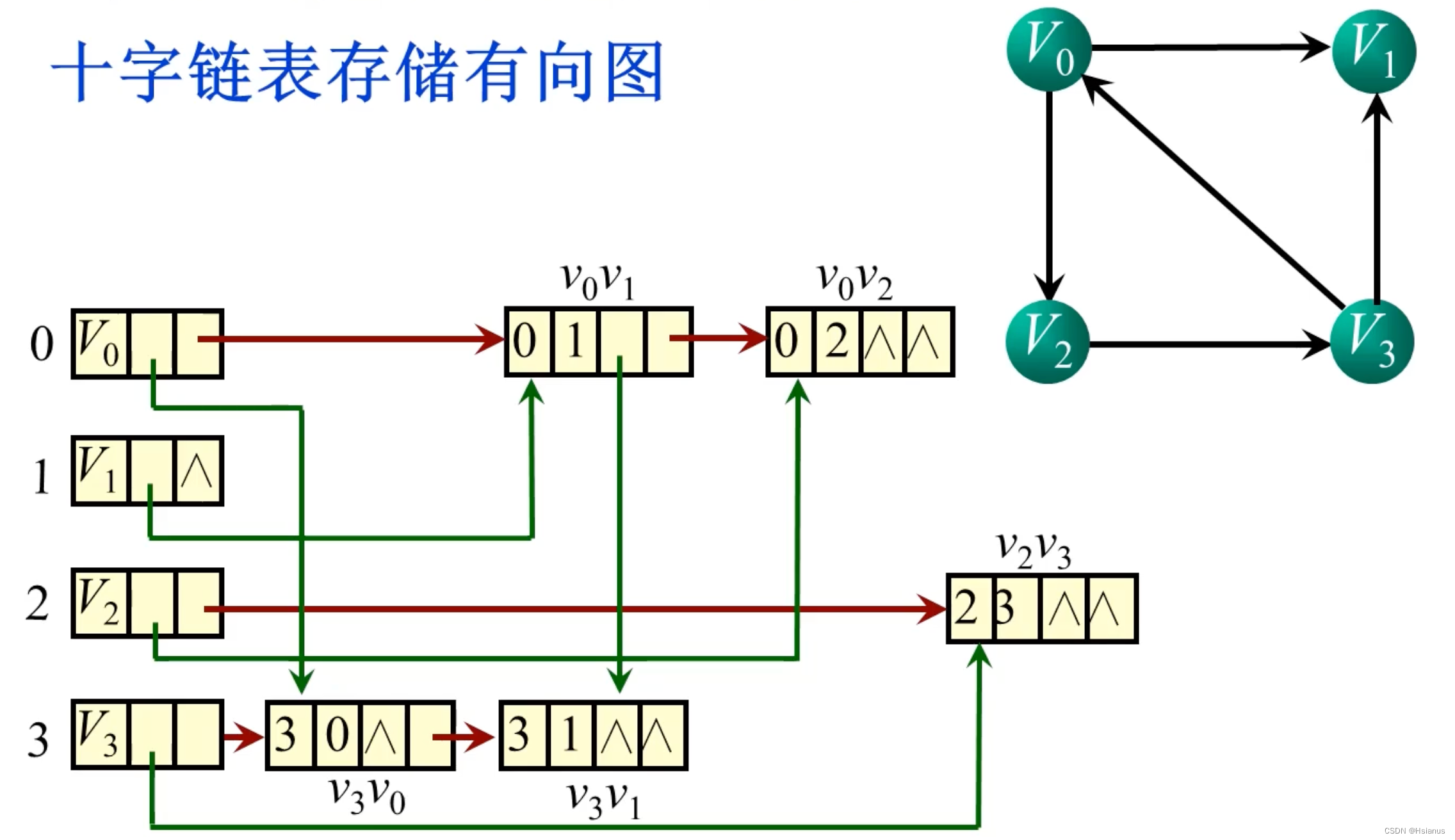
五.十字链表
十字链表的结点结构:

六.图的存储结构的比较