2.机器学习笔记第二周
梯度下降:
就是最优选择算法的图形化表示:一个站在山顶的人,每秒走绝对小的一步,他朝着什么方向移动可以最快到达山脚。
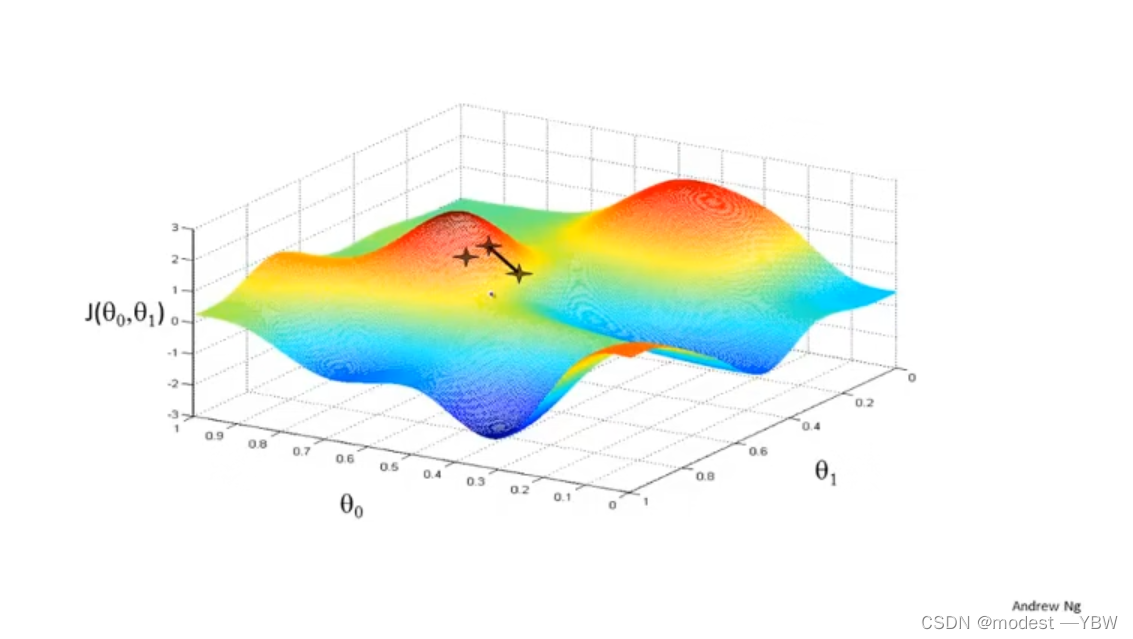
接下来是梯度运算的数学解法:
:=是赋值的意思,a:=b就是a无论什么值,都是等于b
α在此处是学习率,也就是一次性迈多大的步子,决定我们让代价函数一次性下降多大的距离,如果是批量的学习,α是统一的。对于α左边的先保留
下面那个算法是表示同步更新

解释斜率,后面那个导数就代表斜率,所以无论斜率正负,只要是靠近最小值,对算法来说都是有益的尝试

关于学习了α太小或者太大,太小会导致学习速率很慢,很久才能接近最佳点,太大数据有可能不离散,错过最佳点
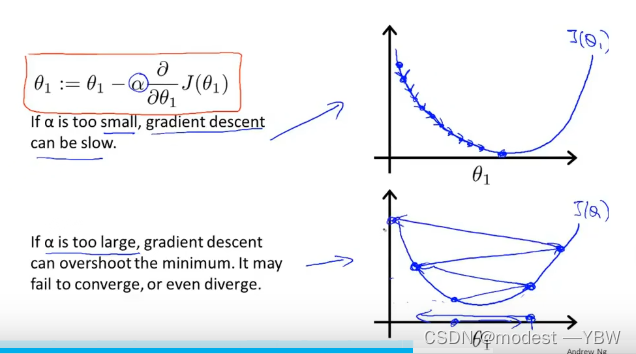
优算法,由于固定学习率α有一些弊端,所以设定学习率减小随着导数减小,就可以很大程度节约开头算力,算力运用效率大大提升。
但是实际上这个是不用,α是一个固定值,而且一旦越接近最低点,导数自然是越来越小,无论是正还是负,都是越趋近最小值越小,所以这个算法很绝妙。
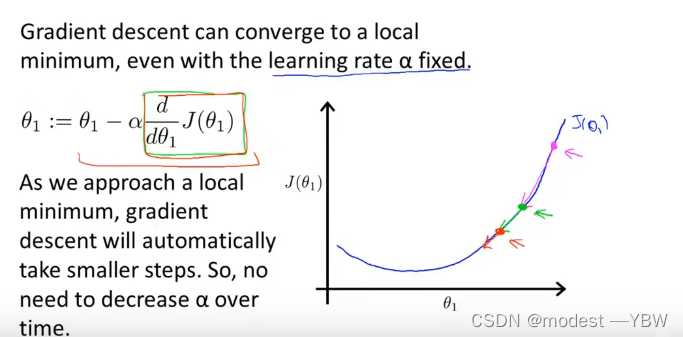
线性回归的梯度下降,将梯度下降算法运用到线性回归里面
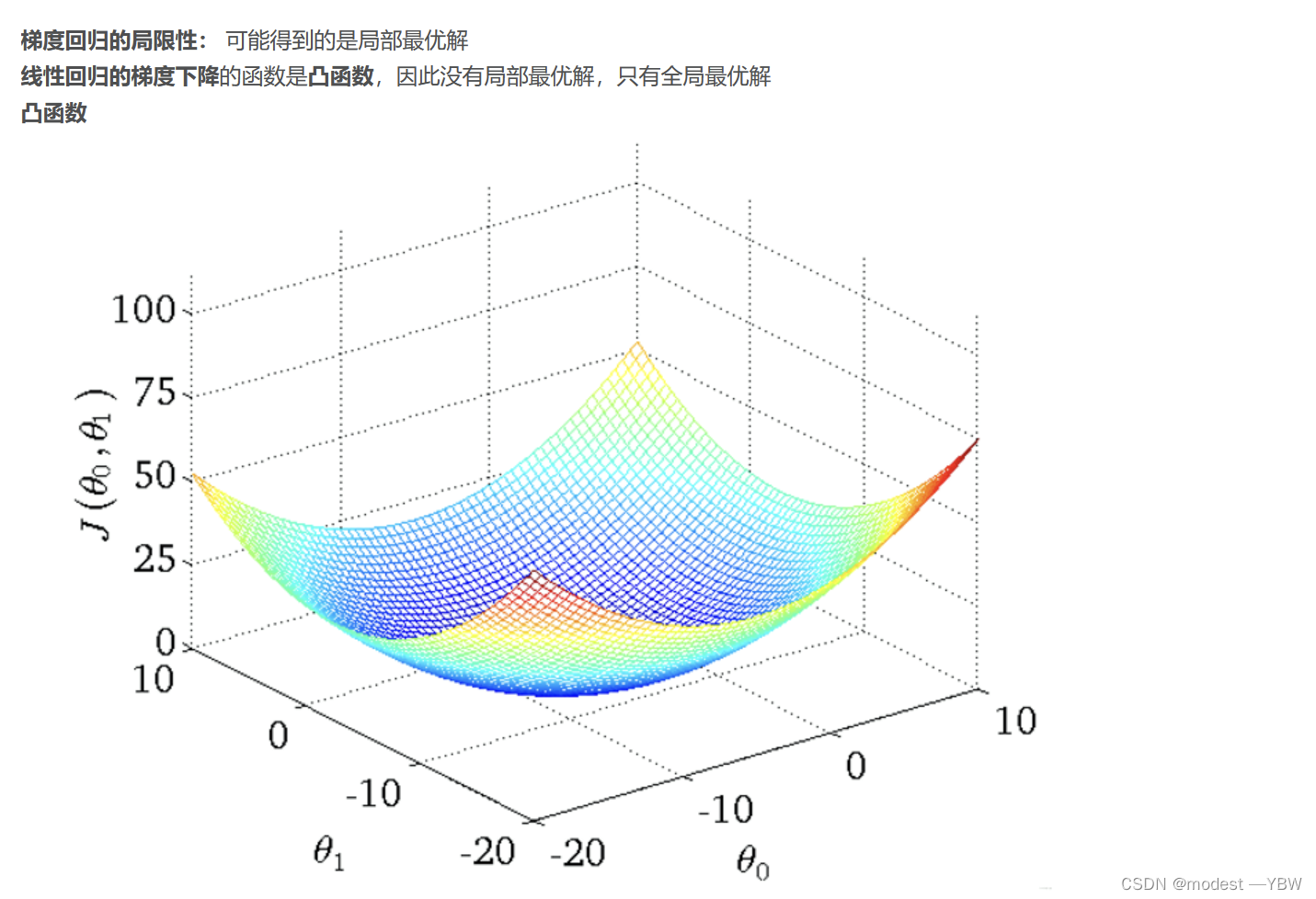
接下来一段为摘抄,我没理解的数学算法

BAD 由于高数不太好,听不懂了,裂开,我学的第一个算法就因为高数学不会了。

本周总结:这周确实没怎么学懂算法,我单独理解了两个分算法的意思,但是在把他们合起来的时候,由于偏导数和一些知识,导致我没有听清楚我学到的第一个算法,很裂开。
