Peter算法小课堂—高精度减法

 给大家看个小视频高精度减法_哔哩哔哩_bilibili

基本思想

计算机模拟人类做竖式计算，从而得到正确答案

大家还记得小学时学的“减法竖式”吗？是不是这样

x-y问题

函数总览：

1.converts() 字符串转为高精度大数

2.le() 判断大小

3.sub() 将两个高精度大数相减

4.print() 输出一个高精度大数（删除前导0）

易错点

1.相减为负数时的处理

2.减法借位的处理

3.删除前导0

main()

int x[SIZE],y[SIZE];
int main(){
	string s1,s2;
	cin>>s1>>s2;
	converts(x,s1);
	converts(y,s2);
	if(le(y,x)){
		sub(x,y);
		print(x);
	}
	else{
		sub(y,x);
		cout<<"-";print(y);
	}
	return 0;
}

le()

bool le(int *a,int *b,int len=SIZE){
	int i;
	for(i=len-1;i>=0&&a[i]==b[i];i--);//判断等于 
	return i<0||a[i]<b[i];
}

方法图示

sub()

void sub(int *a,int *b,int len=SIZE){
	for(int i=0;i<len;i++)
		if((a[i]-=b[i])<0){
			a[i+1]--;
			a[i]+=10;
		}
}

借位图示

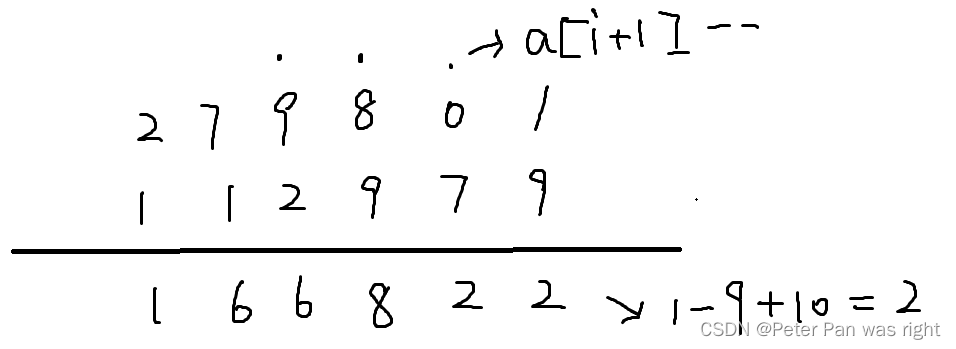
代码

#include <bits/stdc++.h>
using namespace std;
#define SIZE 550
int x[SIZE],y[SIZE];
void converts(int *a,string s){
	int i,len=s.size();
	for(i=0;i<len;i++) a[i]=s[len-i-1]-'0';
	for(;i<SIZE;i++) a[i]=0;
}
bool le(int *a,int *b,int len=SIZE){
	int i;
	for(i=len-1;i>=0&&a[i]==b[i];i--);//判断等于 
	return i<0||a[i]<b[i];
}
void sub(int *a,int *b,int len=SIZE){
	for(int i=0;i<len;i++)
		if((a[i]-=b[i])<0){
			a[i+1]--;
			a[i]+=10;
		}
}
void print(int *a){
	int i;
	for(i=SIZE-1;i>0;i--) if(a[i]>0) break;
	for(;i>=0;i--) cout<<a[i];
	cout<<endl;
}
int main(){
	string s1,s2;
	cin>>s1>>s2;
	converts(x,s1);
	converts(y,s2);
	if(le(y,x)){
		sub(x,y);
		print(x);
	}
	else{
		sub(y,x);
		cout<<"-";print(y);
	}
	return 0;
}

希望这些对大家有用，三连必回