经典文献阅读之--Traversability Analysis for Autonomous Driving...(Lidar复杂环境中的可通行分析)
0. 简介
对于自动驾驶来说,复杂环境的可通行是最需要关注的任务。《Traversability Analysis for Autonomous Driving in Complex Environment: A LiDAR-based Terrain Modeling Approach》一文提出了用激光雷达完成建图的工作,其可以输出稳定、完整和精确的地形建模以及可通行分析结果。由于地形是环境的固有属性,不会随着视角不同而发生变化,因此本文方法采用一种多帧的信息融合策略进行地形建模。具体而言,本文采用一种正态分布变换建图方法,通过融合来自连续激光雷达帧的信息来精确地建模地形。然后利用空间-时间贝叶斯广义核推断和双边滤波来提高结果的稳定性和完整性,同时保留尖锐地形的边缘。基于地形建模结果,通过对相邻地形区域之间进行几何连通性分析来获取每个区域的可通行性。
1. 主要贡献
本文的贡献总结如下:
1)本文充分利用连续激光雷达帧提供的信息进行可通行分析,而不是将其作为一个单帧任务。本文采用一种NDT建图方法对地形进行建模。此外,我们还考虑了全局网格地图和局部网格地图之间的量化误差。通过采用这种多帧融合方法,可以轻易避免一些估计误差,并且估计结果更有可能稳定和完整;
2)本文提出一种空间-时间BGK高度推断方法。与最初的BGK方法相比,我们做出了两点改进。第一点改进为,我们将双边滤波引入到BGK高度推断中,从而缓解了边缘模糊问题。第二点改进为,在BGK推断中引入由NDT建图方法估计的高度方差作为权重。在这个权重的帮助下,具有较大方差的网格单元对高度推断的贡献越少。通过应用这两点改进,估计的地形模型和可通行分析结果可以更为精确;
3)通过分析相邻地形单元之间的几何连通性质,我们可以获得一张代价地图。这张代价地图有助于区分不同的地形类型,例如路缘、沟渠、坡道和道路边界。因此,本文所提出的方法可以帮助UGV路径规划模块在复杂环境中选择合理且安全的路径。
2. 方法总结
所提出的可行性分析方法的框架如图2所示。输入是来自姿态估计模块[Xue et al., 2019]的LiDAR点云和高频6自由度(DoF)姿态序列,该模块融合了惯性导航系统(INS)、轮编码器和LiDAR里程计的信息。该方法的输出是一个密集的地形模型和局部环境的代价地图。地形模型由法向量图和密集的高程图表示。 所提出的方法主要包括四个模块:数据预处理和粗分割模块、高程估计模块、高程预测和细化模块以及可行性分析模块。这四个模块的详细内容如下所述。
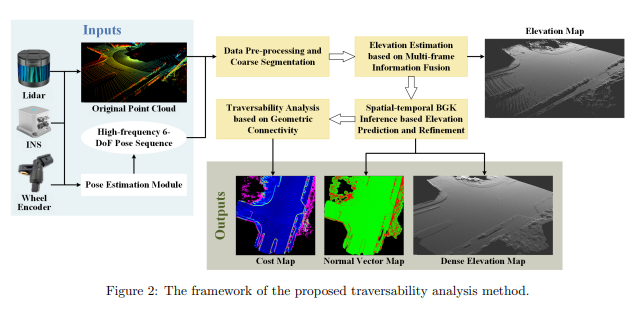
图2:所提出的可行性分析方法的框架
2. 数据预处理和粗分割
众所周知,随着UGV在一次LiDAR扫描期间移动,LiDAR点云会发生扭曲。为了纠正扭曲的点云,高频6自由度姿态估计模块生成的姿态被用于帧内运动补偿。此外,根据6自由度姿态中获取的方位角、横滚角和俯仰角,点云也被旋转到垂直位置。在此旋转后,可以在轴对齐坐标中很好地估计地形属性(如法向量、坡度等)。 然后,矫正后的点云被投影到一个2D网格地图中,并利用最小-最大高度差方法[Thrun et al., 2006]将网格单元粗略分类为地形单元和非地形单元。在这种方法中,需要设置一个高度差阈值Th(该阈值的设置在表2中列出)。如果网格单元的最小-最大高度差大于Th,则被认为是障碍单元。此外,还利用[Jaspers et al., 2017]中介绍的方法从点云中去除悬挂结构。
在这个粗分类之后,2D网格地图被分为三个部分:障碍网格单元、潜在地形网格单元和未观测到的网格单元。在这个阶段,值得一提的是,潜在地形网格单元可能包含误报。例如,附近车辆的车顶可能被错误地判断为潜在地形单元。这些错误可能不容易通过处理单个LiDAR帧来纠正,但可以通过采用后续子节中描述的多帧信息融合策略来轻松避免。 对于每个潜在地形网格单元
x
i
x_i
xi,其观测到的高度可以通过融合落在该网格单元中的所有
n
i
n_i
ni个点的观测高度
{
z
i
,
j
}
j
=
1
:
n
i
\{z_i,j\}_{j=1:n_i}
{zi,j}j=1:ni来建模为正态分布
N
(
µ
i
,
Σ
i
)
N(µ_i, Σ_i)
N(µi,Σi):
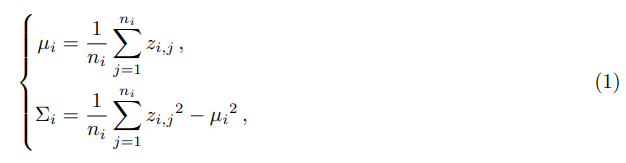
其中
µ
i
µ_i
µi和
Σ
i
Σ_i
Σi分别是
N
(
µ
i
,
Σ
i
)
N(µ_i,Σ_i)
N(µi,Σi)的均值和方差。图3展示了由单个LiDAR帧生成的高程分布的一个说明性例子。
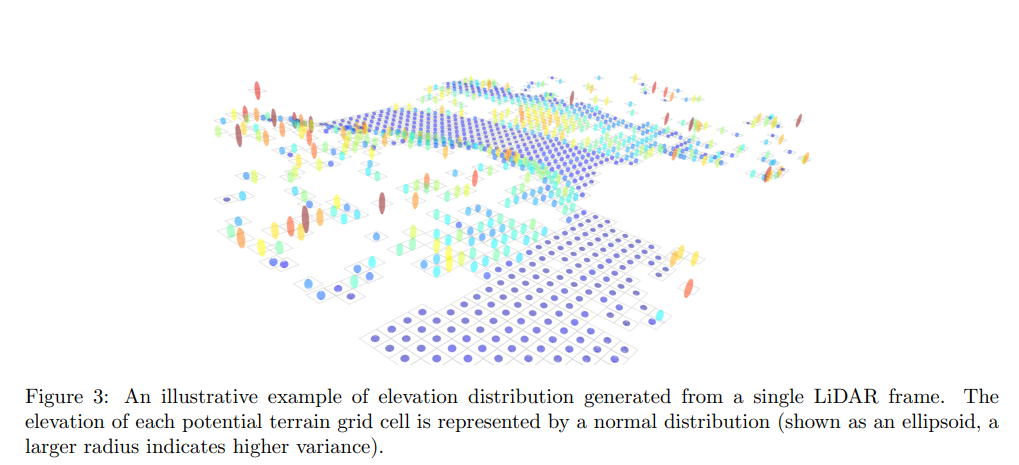
图3:通过单个LiDAR帧生成的高程分布的示例说明。每个潜在地形网格单元的高程由一个正态分布表示(以椭球形式展示,较大的半径表示较高的方差)
3. 基于多帧信息融合的高度估计
为了融合连续的LiDAR帧的信息,采用了滚动网格技术[Behley and Stachniss, 2018]来构建全局网格地图。如图4所示,全局网格地图的大小为
W
×
W
W×W
W×W,每个网格单元表示一个
ω
×
ω
ω×ω
ω×ω的区域,存储在上一个时间步骤
t
−
1
t-1
t−1中估计的高度分布(
W
W
W和
ω
ω
ω的设置在表2中列出)。随着UGV的移动,超出地图边界的历史网格单元将被移除(如图4中的灰色单元),并且在移动方向上生成相同数量的新单元。
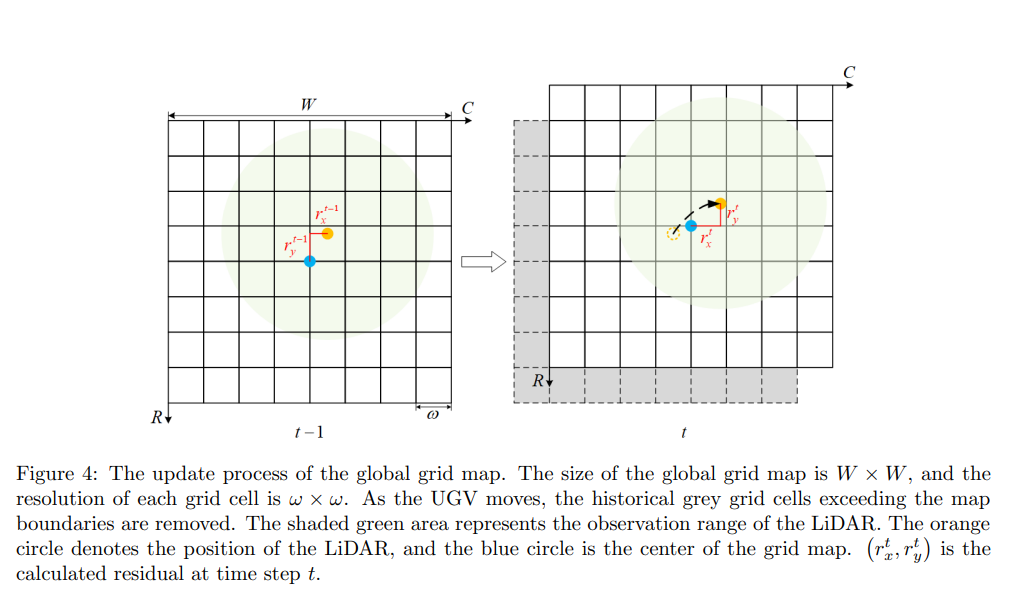
图4:全局栅格地图的更新过程。全局栅格地图的大小为 W × W W×W W×W,每个栅格单元的分辨率为 ω × ω ω×ω ω×ω。随着无人地面车辆的移动,超出地图边界的历史灰色栅格单元将被移除。阴影绿色区域表示激光雷达的观测范围。橙色圆圈表示激光雷达的位置,蓝色圆圈是栅格地图的中心。 ( r x t , r y t ) (r^t_x , r^t_y) (rxt,ryt) 是时间步骤 t t t处计算得到的残差
全局网格地图的中心被定义为LiDAR所在的网格单元的左下角(如图4中的蓝色圆圈所示)。设
(
L
x
t
,
L
y
t
)
(L^t_x , L^t_y)
(Lxt,Lyt)表示LiDAR在全局坐标系中的位置,表示为时间步骤
t
t
t(如图4中的橙色圆圈所示),那么我们可以计算出LiDAR相对于其所在网格单元左下角的残差
(
r
x
t
,
r
y
t
)
(r^t_x , r^t_y)
(rxt,ryt) 。

其中函数Floor(a)是一个取整运算符,返回不大于
a
a
a的最大整数。
由于全局地图的中心始终定义为LiDAR所在的网格单元的左下角,因此计算得到的残差恰好表示LiDAR坐标和全局地图坐标之间的平移偏移量。设
(
p
x
t
,
p
y
t
,
p
z
t
)
(p^t_x , p^t_y , p^t_z)
(pxt,pyt,pzt)表示LiDAR坐标系中的观测点,其全局网格坐标
(
r
,
c
)
(r, c)
(r,c)可以计算得到。
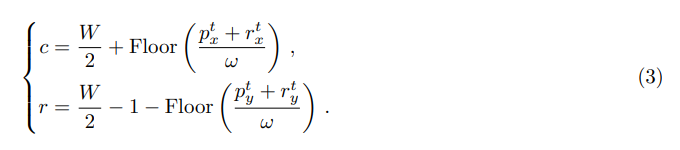
在以往的研究中,点云通常在激光雷达的局部坐标系中进行处理,其中激光雷达地图的中心与激光雷达的原点对齐。该过程的输出通常是一个局部网格地图,然后将其融合到全局网格地图中。在本文中,我们强调全局网格地图是由全局坐标离散化的,因此首先应通过计算得到的残差来补偿激光雷达的局部坐标。借助这个值,激光雷达的局部网格地图将与全局网格地图对齐,从而可以很好地消除由不同激光雷达姿态引起的量化误差。
然后,连续帧的信息将在全局网格地图中融合。对于包含投影点的每个网格单元xi,首先通过公式(1)计算时间戳 t t t下的观测高度分布 N ( µ i t , Σ i t ) N(µ^t_i , Σ^t_i ) N(µit,Σit),并通过将 N ( µ i t , Σ i t ) N(µ^t_i , Σ^t_i ) N(µit,Σit)与先前的联合高度分布 N ^ ( µ ^ i t , Σ ^ i t ) \hat{N}(\hat{µ}^t_i , \hat{Σ}^t_i) N^(µ^it,Σ^it) 进行融合来估计当前的联合高度分布 N ^ ( µ ^ i t − 1 , Σ ^ i t − 1 ) \hat{N}(\hat{µ}^{t-1}_i , \hat{Σ}^{t-1}_i) N^(µ^it−1,Σ^it−1)
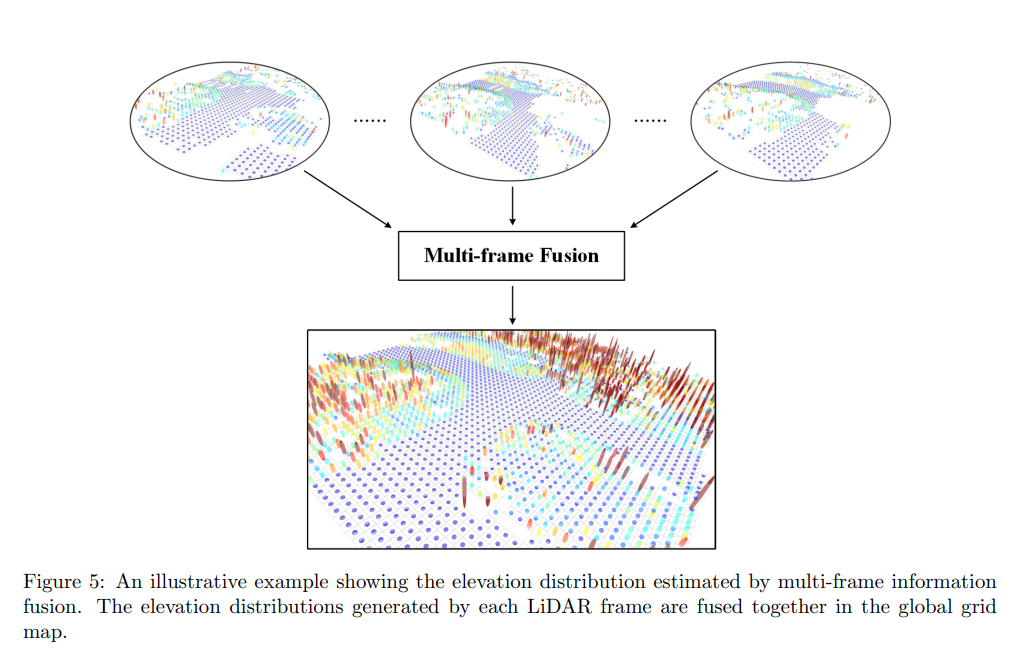
图5:一个说明性的例子,展示了多帧信息融合所估计的高程分布。每个激光雷达帧生成的高程分布在全局网格地图中进行融合
多帧信息融合估计的高程分布的一个说明性例子如图5所示,每个单独的LiDAR帧生成的高程分布在全局网格地图中进行融合,从而得到更稳定和完整的结果。此外,通过稳定的分布方差信息可以对潜在地形区域进行细化分割,如果一个被多次观测到的网格单元的估计方差高于方差阈值 T Σ T_Σ TΣ(该阈值的设置在表2中列出),则该网格单元也将被视为障碍物单元。
4. 基于时空BGK推理的高程预测与细化
这段内容进一步讲述了一个改进的空间-时间BGK推理方法来预测和精化网格单元的高度分布。输入是潜在地形单元集
O
t
O^t
Ot,其中
N
i
t
N_i^t
Nit代表在时间步长
t
t
t处的网格单元
x
i
x_i
xi的预测高度分布,
N
o
t
N^t_o
Not是
O
t
O^t
Ot中的输入样本数量。任务是基于输入
O
t
O^t
Ot估计目标网格单元
x
∗
x_∗
x∗的高度分布
N
∗
t
N^t_∗
N∗t,并将其转化为一个回归问题。
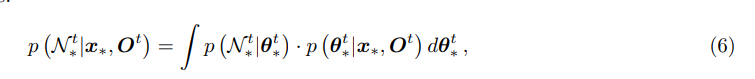
空间-时间BGK推理方法应用了贝叶斯定理、条件独立假设以及一个平滑的扩展似然模型。这个方法也考虑了每个网格单元 x i x_i xi相关的预测方差信息 Σ ˆ t i Σˆt_i Σˆti作为权重。方差较大的网格单元在高度推理过程中的贡献会较小。
空间-时间BGK推理方法的目标是估计目标网格单元
x
∗
x_∗
x∗的高度
h
∗
h_∗
h∗。此外,也采用了边缘保持过滤技术,特别是双边过滤,以解决高斯滤波可能导致边缘模糊的问题。这在地形有明显变化的区域尤其重要。
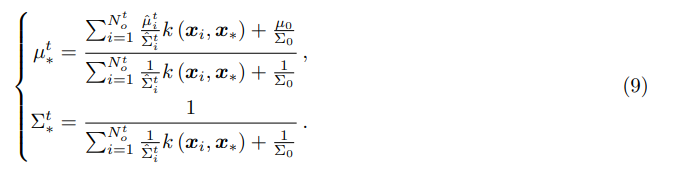
在这个推理过程中,每个潜在地形单元
x
i
x_i
xi的高度首先通过公式(9)进行估计,然后计算估计高度与观察高度之间的差值
δ
i
t
δ^t_i
δit。对于地形有急剧变化的网格单元,差值
δ
i
t
δ^t_i
δit通常会很大。因此,
δ
i
t
δ^t_i
δit被转化为高斯权重
w
i
t
w^t_i
wit。

最后,这个过程是通过图7进行展示的,其中绿色单元代表观测到的潜在地形网格单元,红色单元表示需要估计的目标网格单元。在内核的有效支持范围l(由灰色圆圈颜色表示)内,每个绿色单元对红色单元的估计都有贡献,贡献程度取决于三个因素:在第3.2节中估计的分布方差
Σ
i
t
Σ^t_i
Σit、与红色单元的距离
d
i
d_i
di,以及用于双边过滤的估计-观察差异
δ
i
t
δ^t_i
δit。
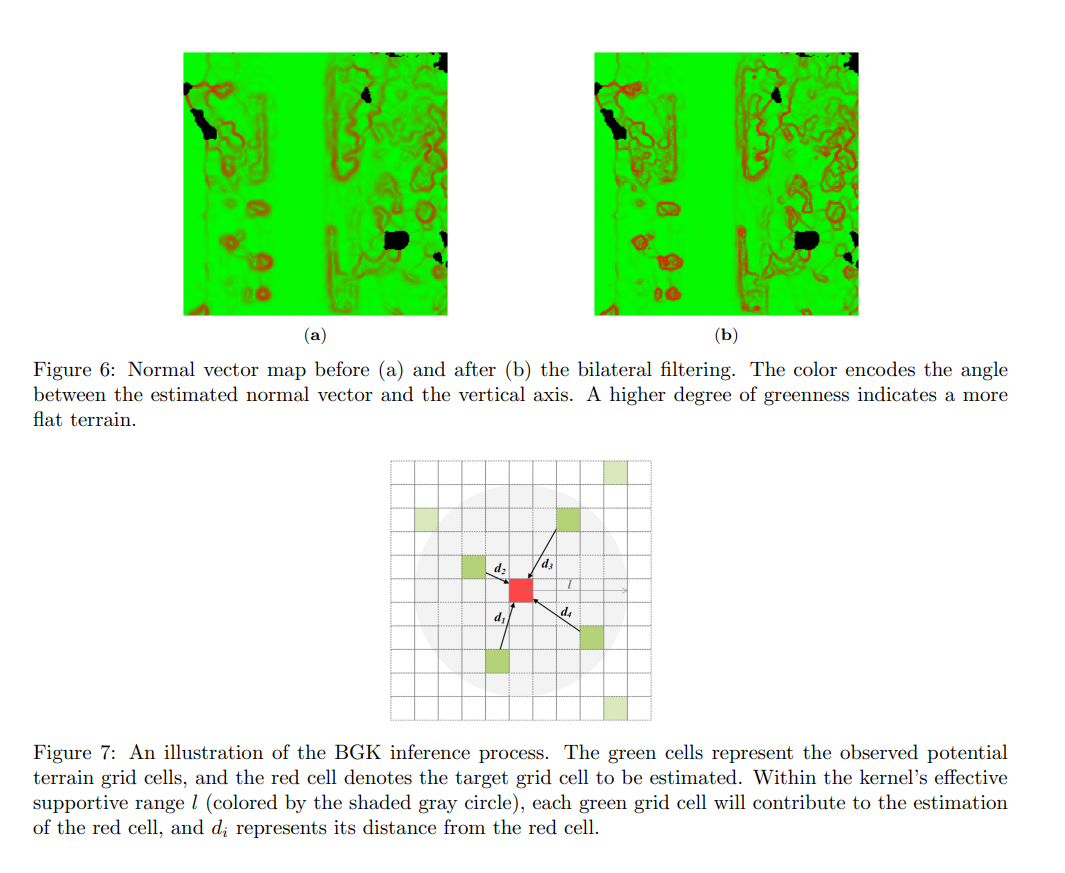
图6:双边滤波前(a)和双边滤波后(b)的法向量图。颜色编码了估计的法向量与垂直轴之间的角度。更高程度的绿色表示更平坦的地形。
图7:BGK推理过程的示意图。绿色单元格表示观测到的潜在地形网格单元格,红色单元格表示待估计的目标网格单元格。在核函数的有效支持范围l内(由阴影灰色圆圈标示),每个绿色网格单元格都会对红色单元格的估计做出贡献, d i d_i di表示它与红色单元格的距离。
