当前位置：首页 > article >正文

算法设计与实现--动态规划篇

article 2024/11/14 20:48:05

什么是动态规划算法

动态规划算法是一种求解复杂问题的方法，通过将原问题分解为相对简单的子问题来求解。其基本思想是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。动态规划算法通常适用于有重叠子问题和最优子结构性质的问题，可以大大减少计算量。

动态规划算法的实现方式包括自底向上的递推和自顶向下的递归，同时需要使用记忆化存储来避免重复计算。动态规划算法可以应用于许多领域，如计算机科学、数学、经济学等。

动态规划算法的优点在于它可以解决一些经典的问题，如背包问题、最大子段和问题、最长公共子序列问题等，并且在一些情况下，它的时间复杂度比朴素解法更优。同时，动态规划算法也可以用于解决一些实际问题，如资源分配、生产调度、图像处理等。

动态规划算法的缺点在于它需要花费大量的时间和空间来存储子问题的解，因此对于一些大规模问题，可能会出现“维度灾难”的情况。此外，动态规划算法的正确性和效率往往取决于问题的定义和状态转移方程的设计，因此需要仔细地分析和设计算法。

总之，动态规划算法是一种重要的算法思想，可以帮助我们解决一些复杂的问题。但是，它并不是万能的，需要根据具体问题的特点来决定是否使用动态规划算法来求解。

动态规划可以简化为下面四个步骤：

问题结构分析：给出问题表示，明确原始问题

递推关系确立：分析最优结构，构造递推关系

自底向上计算：确定计算顺序，依次求解问题

最优方案追踪：记录决策过程，输出最优方案

下面我们用具体的问题来深入的了解动态规划算法。

动态规划相关问题

1、0-1背包问题

问题描述

问题：给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，我们如何选择，才能使得物品的总价值最高

解决思路：

定义状态：
- 定义一个二维数组dp，dp[i][j]表示在前i个物品中，背包容量为j时的最大总价值。
初始化：
- 将dp数组的第一行和第一列初始化为0，表示背包容量为0或物品数量为0时的最大总价值都为0。
状态转移：
- 对于第i个物品，有两种情况：
  - 不放入背包，此时总价值为dp[i-1][j]；
  - 放入背包，此时总价值为dp[i-1][j-w[i]] + v[i]，其中w[i]表示第i个物品的重量，v[i]表示第i个物品的价值。
- 取两种情况中的较大值，即dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])。
最优解：
- 最大总价值为dp[n][C]，其中n为物品的数量，C为背包的容量

用动态规划的思想

1、问题结构分析：

p[i][c] : 前i个样品可选，背包容量为 c 时的最大总价格

p[n][c]:前n个样品可选，背包容量为 c 时的最大总价格

2、递推关系确立

最优子结构性质：问题的最优解由相关子问题最优解组合而成，子问题可以独立求解

3、确定计算顺序

4、最优方案追踪

代码实现

#include <stdio.h>

// 返回两个整数中的较大值
int max(int a, int b) {
    return (a > b) ? a : b;
}

// 0-1背包问题的动态规划解法
// W 表示背包的承载量，wt[],是物品的重量，val[]是物品的价值，n 是物品的总数
int knapsack(int W, int wt[], int val[], int n) {  
    int dp[n + 1][W + 1];  // 创建动态规划表

    // 填充动态规划表
    for (int i = 0; i <= n; i++) {
        for (int w = 0; w <= W; w++) {
            if (i == 0 || w == 0) {
                dp[i][w] = 0;  // 边界条件，背包容量为0或没有物品可选时，价值为0
            } else if (wt[i - 1] <= w) {
            	// 如果背包的容量够，那么就有两种可能，一种是选择该件商品，一种是不选择该件商品
				// 如果选择该件商品，那么需要记录背包中的总价值，并且记录背包的剩余容量
				// 如果不选择该件商品，就直接返回原来的背包容量
				// 然后进行比较，返回价值较大的选择 
                dp[i][w] = max(val[i - 1] + dp[i - 1][w - wt[i - 1]], dp[i - 1][w]);
            } else {
                // 如果背包容量不够，那就不能选择商品
                dp[i][w] = dp[i - 1][w];
            }
        }
    }

    return dp[n][W];  // 返回最大价值
}

int main() {
    int val[] = {60, 100, 120};  // 物品的价值
    int wt[] = {10, 20, 30};  // 物品的重量
    int W = 50;  // 背包的容量
    int n = sizeof(val) / sizeof(val[0]);

    int maxVal = knapsack(W, wt, val, n);
    printf("背包中物品的最大总价值为：%d\n", maxVal);

    return 0;
}

2、最大子数组问题

这个在前面一章中也提到过，在这个文章中用的是分治的思想

算法设计与实现--分治篇-CSDN博客

最大子数组问题是指在一个一维数组中找到和最大的连续子数组

算法思路

1、问题结构分析：

2、递推关系确立

3、自底向上计算

4、最优方案追踪

算法实现

/*
思路：
1、定义一个动态规划数组 D，其中 D[i] 表示以第 i 个元素结尾的最大子数组和。、
2、递推关系是关键，它告诉我们如何通过已知信息计算新的信息：D[i] = max(D[i-1] + num[i], num[i])
意思是，要计算以第 i 个元素结尾的最大子数组和，我们可以选择继续扩展前面的子数组，或者从当前元素重新开始一个新的子数组
就是说，假如说 我们现在知道D[2] = 3 就是第2个元素结尾的最大子数组和是3，然后就是现在要求D[3],D[3] = max(D[3-1] + num[3], num[3]),就是说，原本的子数组和 + 下一个数组元素，和原来的数组元素比较大小，大的话就记录下来。以此类推，直到遍历完整个数组。

*/


# include <stdio.h>

int max(int a,int b){
	if(a>b){
		return a;
	}else{
		return b;
	}
}


int maxSubArray(int* num,int size){
	if(size == 0){
		return 0;
	}
	int D[size];
	D[0] = num[0];  // 动态规划数组，D[i]表示以第i个元素结尾的最大子数组和
	int maxSum = D[0];  // 初始化第一个元素
    // 从第二个元素开始遍历数组，根据递推关系更新动态规划数组
	for(int i = 1;i<size;i++){
		D[i] = max((D[i-1]+num[i]),num[i]);
		
		if(maxSum < D[i]){
			maxSum = D[i];
		}
	}
	return maxSum;
}

int main(){
	
	
	int nums[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
    int size = sizeof(nums) / sizeof(nums[0]);

    int result = maxSubArray(nums, size);

    printf("Maximum Subarray Sum: %d\n", result);
	
	return 0;
}

3、最长公共子序列问题

问题描述

最长公共子序列（Longest Common Subsequence，简称LCS）问题是一个经典的计算机科学问

题，通常用于比较两个序列之间的相似性

算法思路

假设有两个序列，分别为序列A和序列B，长度分别为m和n。

1、创建一个二维数组dp，大小为(m+1)×(n+1)，用于存储中间结果。dp[i][j]表示序列A的前i个元素和序列B的前j个元素的LCS的长度。

2、初始化第一行和第一列的值为0，即dp[0][j] = dp[i][0] = 0。

3、使用动态规划的思想，依次计算dp[i][j]的值。遍历i从1到m，遍历j从1到n。

如果A[i]等于B[j]，则说明A[i]和B[j]可以作为LCS的一个元素，所以dp[i][j] = dp[i-1][j-1] + 1。

如果A[i]不等于B[j]，则说明A[i]和B[j]不能同时作为LCS的元素，此时需要做选择：

如果选择包含A[i]，则LCS的长度不变，即dp[i][j] = dp[i-1][j]；

如果选择包含B[j]，则LCS的长度不变，即dp[i][j] = dp[i][j-1]；

综合考虑，取两种选择中的较大值，即dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

4、遍历完所有的元素后，dp[m][n]即为序列A和序列B的LCS的长度。

5、可以通过回溯dp数组的路径，得到LCS的具体内容。从dp[m][n]开始，根据dp数组的值和状态转移方程进行回溯，如果dp[i][j]等于dp[i-1][j-1]+1，则A[i]和B[j]是LCS的一个元素，将其加入结果序列中，并继续回溯dp[i-1][j-1]；如果dp[i][j]等于dp[i-1][j]，则表示A[i]不是LCS的元素，继续回溯dp[i-1][j]；如果dp[i][j]等于dp[i][j-1]，则表示B[j]不是LCS的元素，继续回溯dp[i][j-1]。重复以上步骤，直到回溯到dp[0][0]，即可得到LCS的内容。

代码实现

#include <stdio.h>
#include <string.h>

#define MAX_LENGTH 100

int max(int a, int b) {
    return (a > b) ? a : b;
}

void longestCommonSubsequence(char* A, char* B) {
	
	int m = strlen(A);
    int n = strlen(B);
	
    int dp[m+1][n+1];
    int i, j;

    // 初始化dp数组
    for (i = 0; i <= m; i++) {
        for (j = 0; j <= n; j++) {
            if (i == 0 || j == 0)
                dp[i][j] = 0;
            else if (A[i - 1] == B[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }

    // 回溯dp数组，构造LCS
    int index = dp[m][n];   // 得到最长公共子序列的长度
    char lcs[index + 1];  
    lcs[index] = '\0';
    i = m;
    j = n;
    while (i > 0 && j > 0) {
        if (A[i - 1] == B[j - 1]) { // 说明这个字符在LCS中，我们将其放入lcs数组的当前位置index - 1，然后将i和j都减1，继续向前回溯。
            lcs[index - 1] = A[i - 1]; 
            i--;
            j--;
            index--;
        }
        else if (dp[i - 1][j] > dp[i][j - 1])
            i--;
        else
            j--;
    }

    printf("Longest Common Subsequence: %s\n", lcs);
    printf("Length of LCS: %d\n", dp[m][n]);
}


int main() {
    char A[MAX_LENGTH];
    char B[MAX_LENGTH];

    printf("Enter sequence A: ");
    scanf("%s", A);
    printf("Enter sequence B: ");
    scanf("%s", B);
	longestCommonSubsequence(A, B);

    return 0;
}

4、最长公共子串

问题描述和算法思路

最长公共子串（Longest Common Substring）问题是另一个经典的计算机科学问题，与最长公共子序列（LCS）问题类似，但要求子串在原序列中是连续的。下面是解决最长公共子串问题的一种常见思路：

假设有两个序列，分别为序列A和序列B，长度分别为m和n。

1、创建一个二维数组dp，大小为(m+1)×(n+1)，用于存储中间结果。dp[i][j]表示以序列A的第i个元素和序列B的第j个元素为结尾的最长公共子串的长度。

2、初始化第一行和第一列的值为0，即dp[i][0] = dp[0][j] = 0。

3、使用动态规划的思想，依次计算dp[i][j]的值。遍历i从1到m，遍历j从1到n。

如果A[i]等于B[j]，说明A[i]和B[j]可以作为公共子串的一部分，所以dp[i][j] = dp[i-1][j-1] + 1。

如果A[i]不等于B[j]，说明以A[i]和B[j]为结尾的子串不连续，此时dp[i][j] = 0。

4、在计算过程中，记录最长公共子串的长度和结束位置。遍历dp数组，如果dp[i][j]大于最长公共子串的长度，则更新最长公共子串的长度和结束位置。

5、最长公共子串的起始位置可以通过最长公共子串的结束位置和长度计算得到。

算法实现

#include <stdio.h>
#include <string.h>

// 定义最大字符串长度
#define MAX_LENGTH 100

void longestCommonSubstring(char* A, char* B) {
    int m = strlen(A);
    int n = strlen(B);

    // 创建二维数组并初始化为 0
    int dp[m+1][n+1] = {0};
    int maxLength = 0;  // 最长公共子串的长度
    int endIndex = 0;   // 最长公共子串的结束位置

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (A[i - 1] == B[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > maxLength) {
                    maxLength = dp[i][j];
                    endIndex = i - 1;
                }
            }
        }
    }

    if (maxLength == 0) {
        printf("没有找到公共子串。\n");
    } else {
        printf("最长公共子串为：");
        for (int i = endIndex - maxLength + 1; i <= endIndex; i++) {
            printf("%c", A[i]);
        }
        printf("\n");
        printf("最长公共子串的长度为：%d\n", maxLength);
    }
}

int main() {
    char str1[MAX_LENGTH];
    char str2[MAX_LENGTH];

    // 从标准输入读取两个字符串
    printf("请输入第一个字符串：");
    fgets(str1, sizeof(str1), stdin);
    printf("请输入第二个字符串：");
    fgets(str2, sizeof(str2), stdin);

    // 去除换行符
    str1[strcspn(str1, "\n")] = '\0';
    str2[strcspn(str2, "\n")] = '\0';

    // 调用函数求解最长公共子串
    longestCommonSubstring(str1, str2);

    return 0;
}

5、编辑距离问题

问题描述

编辑距离（Edit Distance），也称为Levenshtein距离，是衡量两个字符串之间相似程度的一种度量方法。它表示通过插入、删除和替换操作，将一个字符串转换为另一个字符串所需的最少操作次数。

具体而言，编辑距离定义了三种基本操作：

插入（Insertion）：在一个字符串中插入一个字符。
删除（Deletion）：从一个字符串中删除一个字符。
替换（Substitution）：将一个字符替换为另一个字符。

通过执行这些操作，我们可以将一个字符串转换为另一个字符串。编辑距离是执行这些操作的最少次数。

例如，考虑将字符串"kitten"转换为字符串"sitting"。可以通过以下操作实现转换：

替换"k"为"s"。
插入"i"。
插入"g"。

因此，执行这些操作的最小次数为3，因此编辑距离为3

动态规划思想

1、问题结构分析

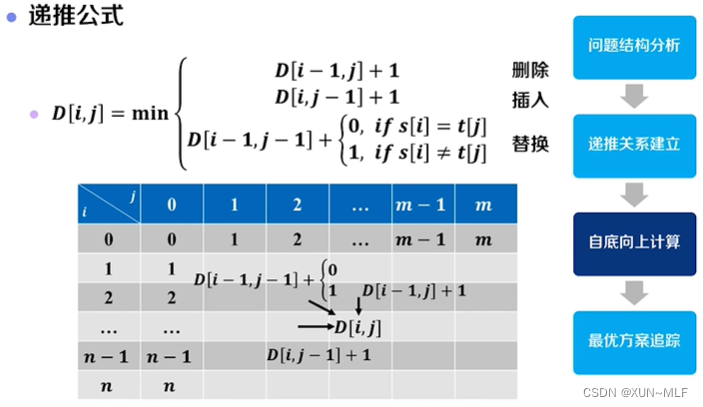
2、递推关系建立

3、自底向上计算

4、最优方案最终

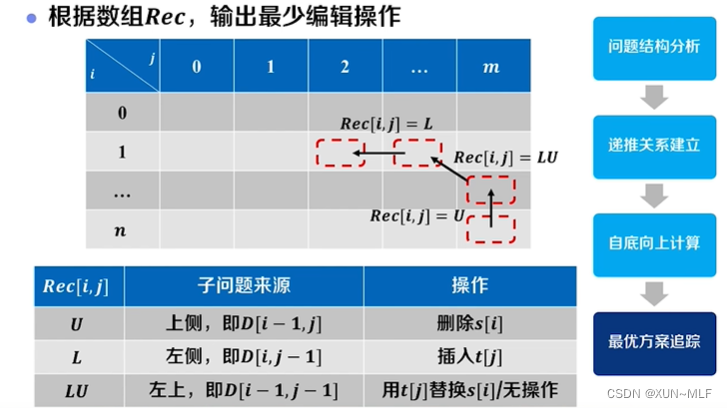
算法思想

计算两个字符串的编辑距离可以使用动态规划算法来解决。下面是一种常见的解题思路：

创建一个二维数组dp，大小为(m+1) × (n+1)，其中m和n分别为两个字符串的长度。dp[i][j]表示将字符串A的前i个字符转换为字符串B的前j个字符所需的最小操作次数。
初始化边界条件：
- 当i=0时，dp[0][j] = j，表示将空字符串转换为字符串B的前j个字符所需的操作次数为j。
- 当j=0时，dp[i][0] = i，表示将字符串A的前i个字符转换为空字符串所需的操作次数为i。
对于i从1到m，和j从1到n，执行以下操作：
- 如果A[i-1]等于B[j-1]，则dp[i][j] = dp[i-1][j-1]，即不需要进行任何操作。
- 否则，dp[i][j]等于以下三个值的最小值加1：
  - dp[i-1][j] + 1，表示将字符串A的前i-1个字符转换为字符串B的前j个字符所需的操作次数，再执行删除操作。
  - dp[i][j-1] + 1，表示将字符串A的前i个字符转换为字符串B的前j-1个字符所需的操作次数，再执行插入操作。
  - dp[i-1][j-1] + 1，表示将字符串A的前i-1个字符转换为字符串B的前j-1个字符所需的操作次数，再执行替换操作。
最终，dp[m][n]即为将字符串A转换为字符串B所需的最小操作次数，即编辑距离。

算法实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 返回三个数中的最小值
int min(int a, int b, int c) {
    if (a <= b && a <= c) {
        return a;
    } else if (b <= a && b <= c) {
        return b;
    } else {
        return c;
    }
}

// 计算字符串的编辑距离
int editDistance(const char* A, const char* B) {
    int m = strlen(A);
    int n = strlen(B);

    // 创建二维数组来存储状态转移表
    /* 
    由于 C 语言中没有直接支持动态分配二维数组的语法，我们需要手动进行内存分配
	我们使用 malloc 函数分配了一段大小为 (m + 1) * sizeof(int*) 字节的内存空间，
	用于存储指向每行的指针
	这一部分的内存分配是为了创建二维数组的行。
	*/
    int** dp = (int**)malloc((m + 1) * sizeof(int*));  // 注意最后面的sizeof(int*) 这个*一定要加上
    
//    int** dp = (int**)malloc((m+1)*sizeof(int*));
    /*我们使用一个循环遍历每一行，
	并分别为每一行分配了 (n + 1) * sizeof(int) 字节的内存空间。这
	一部分的内存分配是为了创建二维数组的列。
	*/
    for (int i = 0; i <= m; i++) {
        dp[i] = (int*)malloc((n + 1) * sizeof(int));
    }

    // 初始化边界条件
    for (int i = 0; i <= m; i++) {
        dp[i][0] = i;
    }
    for (int j = 0; j <= n; j++) {
        dp[0][j] = j;
    }

    // 动态规划计算最小编辑距离
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (A[i - 1] == B[j - 1]) {
                // 字符相等，不需要进行操作
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                // 字符不相等，选择插入、删除或替换操作中的最小值
                dp[i][j] = min(dp[i - 1][j] + 1,    // 删除操作
                               dp[i][j - 1] + 1,    // 插入操作
                               dp[i - 1][j - 1] + 1);  // 替换操作
            }
        }
    }

    int distance = dp[m][n];  // 最终的编辑距离

    // 释放动态分配的内存
    for (int i = 0; i <= m; i++) {
        free(dp[i]);
    }
    free(dp);

    return distance;
}

int main() {
    const char* A = "kitten";
    const char* B = "sitting";
    int distance = editDistance(A, B);
    printf("Edit Distance: %d\n", distance);  // 输出 3

    return 0;
}

6、钢条切割问题

假设有一根长度为 n 英寸的钢条和一个价格表，价格表中列出了每个长度的钢条对应的价格。我们希望确定如何切割钢条，使得销售收益最大化。

算法思路

定义子问题：钢条切割问题的子问题可以定义为：对于长度为 n 的钢条，求其切割方案能够获得的最大收益。
确定状态：钢条切割问题的状态就是钢条的长度 n，需要求解的是长度为 n 的钢条的最大收益。
确定状态转移方程：假设钢条的长度为 n，可以考虑将钢条切割成两部分：长度为 i 和长度为 n-i，其中 0 < i < n。则钢条长度为 n 的最大收益可以通过比较不同切割方案的收益并取最大值来得到，即：

`max_profit = max(price[i] + cutRod(price, n-i))，其中 price[i]表示长度为i 的钢条的价格，cutRod(price, n-i)表示长度为n-i 的钢条的最大收益。

这里使用了递归的方式来解决子问题，通过不断地将原问题划分为更小的子问题并求解子问题的最优解。
确定基本情况：基本情况是切割长度为 0 的钢条，它的收益为 0。
自顶向下计算最优解：通过递归方式，不断将原问题划分为更小的子问题，并利用已经计算过的子问题的最优解，以减少重复计算。
返回最优解：最终的最优解即为长度为 n 的钢条的最大收益。

算法实现

#include <stdio.h>
#include <stdlib.h>


int max(int a,int b){
	return (a>b)?a:b;
}


int cutRod(int price[], int n) {
    int *dp = (int*)malloc((n + 1) * sizeof(int)); // 创建存储最优解的数组

    dp[0] = 0; // 初始条件，长度为 0 的钢条的最大收益为 0

    // 自底向上计算每个状态对应的最大收益
    for (int i = 1; i <= n; i++) {
        int max_val = -1; // 最大收益初始值为 -1
        for (int j = 1; j <= i; j++) {
            // 比较不同切割方案的收益并取最大值
            max_val = max(price[j] + dp[i - j] , max_val);
        }
        dp[i] = max_val; // 保存状态 i 对应的最大收益
    }

    int max_profit = dp[n]; // 最大收益即为长度为 n 的钢条的最大收益

    free(dp); // 释放动态分配的内存

    return max_profit;
}

int main() {
    int price[] = {0, 2, 5, 9, 10};
    int n = 5;
    int max_profit = cutRod(price, n);
    printf("最大收益：%d\n", max_profit);

    return 0;
}

7、矩阵链乘法问题

算法思路

定义子问题：矩阵链乘法问题的子问题可以定义为：对于一组矩阵链 A1, A2, ..., An，求解计算这个矩阵链的最小代价。
确定状态：矩阵链乘法问题的状态可以由两个下标 i 和 j 表示，表示计算矩阵链从第 i 个矩阵到第 j 个矩阵的最小代价。
确定状态转移方程：假设矩阵链的长度为 n，可以考虑将矩阵链划分为两部分：A[i...k] 和 A[k+1...j]，其中 i <= k < j。则计算矩阵链 A[i...j] 的最小代价可以通过比较不同划分方案的代价并取最小值来得到，即：

`dp[i][j] = min(dp[i][k] + dp[k+1][j] + cost(A[i...k], A[k+1...j]))，其中 dp[i][j]表示计算矩阵链A[i...j] 的最小代价，cost(A[i...k], A[k+1...j])表示计算矩阵A[i...k]和A[k+1...j] 的乘积所需的代价。
确定初始条件和边界情况：初始条件是 dp[i][i] = 0，表示计算单个矩阵的乘积不需要任何代价。边界情况是 i = j，此时矩阵链只有一个矩阵，也不需要进行乘积计算。
自底向上计算最优解：根据状态转移方程，我们可以从较小的子问题开始逐步求解更大的问题，直到求解出整个问题的最优解。具体做法是使用一个二维数组 dp 来保存每个状态对应的最小代价，从小到大依次计算 dp[i][j]。
返回最优解：最终的最优解存储在 dp[1][n] 中，表示计算整个矩阵链的最小代价。

算法实现

#include <stdio.h>
#include <limits.h>

#define MAX_SIZE 100

void matrixChainOrder(int p[], int n, int m[MAX_SIZE][MAX_SIZE], int s[MAX_SIZE][MAX_SIZE]) {
    int i, j, k, l, q;

    // 初始化代价矩阵和分割点矩阵
    for (i = 1; i <= n; i++) {
        m[i][i] = 0;
    }

    // 计算代价和分割点
    for (l = 2; l <= n; l++) {
        for (i = 1; i <= n - l + 1; i++) {
            j = i + l - 1;
            m[i][j] = INT_MAX;
            for (k = i; k <= j - 1; k++) {
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (q < m[i][j]) {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
        }
    }
}

void printOptimalParentheses(int s[MAX_SIZE][MAX_SIZE], int i, int j) {
    if (i == j) {
        printf("A%d", i);
    } else {
        printf("(");
        printOptimalParentheses(s, i, s[i][j]);
        printOptimalParentheses(s, s[i][j] + 1, j);
        printf(")");
    }
}

int main() {
    int p[MAX_SIZE] = {10, 30, 5, 60};
    int n = 3; // 矩阵链的数量

    int m[MAX_SIZE][MAX_SIZE];
    int s[MAX_SIZE][MAX_SIZE];

    matrixChainOrder(p, n, m, s);

    printf("最小代价：%d\n", m[1][n]);
    printf("最优括号化方案：");
    printOptimalParentheses(s, 1, n);
    printf("\n");

    return 0;
}

查看全文

http://www.kler.cn/a/156141.html