排序:直接插入排序希尔排序
目录
排序:
概念:
直接插入排序:
代码的实现:
代码解析:
总结:
希尔排序:
代码实现:
预排序:
代码优化:
gap 的 本质 :
直接插入排序:
代码图解:
总结:

排序:
概念:
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
而通过排序中的元素交换次数和排序所需要的次数,排序可以分为两层:
- 内部排序:数据元素全部放在内存中的排序。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
直接插入排序:
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。
- 简单来说,直接插入排序的前提是需要有一个有序的序列作为基础。

实际中我们玩扑克牌时,就用了插入排序的思想
代码的实现:
代码的实现本质上也分为内外两层结构。
直接插入排序的内层是用来实现有序序列的排序,而直接插入排序的外层则是用来扩大排序的范围。

代码解析:

如图所示,以升序为例,直接插入排序的内层进行寻找插入元素应当插入的位置和对原来排序中的元素进行移位,以此保持插入元素后仍能保持有序。
插入排序的外层是进行引入 插入的元素和扩大有序排序的范围,以此将整个数组变为 一个有序排序。
总结,通过内层将一个无序数组的一部分变成有序排序,通过外层扩大有序排序的范围最后将整个数组变成有序数组。

总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
希尔排序:
希尔排序分为预排序和直接插入排序
- 预排序是又称接近有序排序的排序,它是将数组内的元素进行分组,每一组内进行直接插入排序。
- 当每一组都完成排序后,在对整个数组进行直接插入排序。

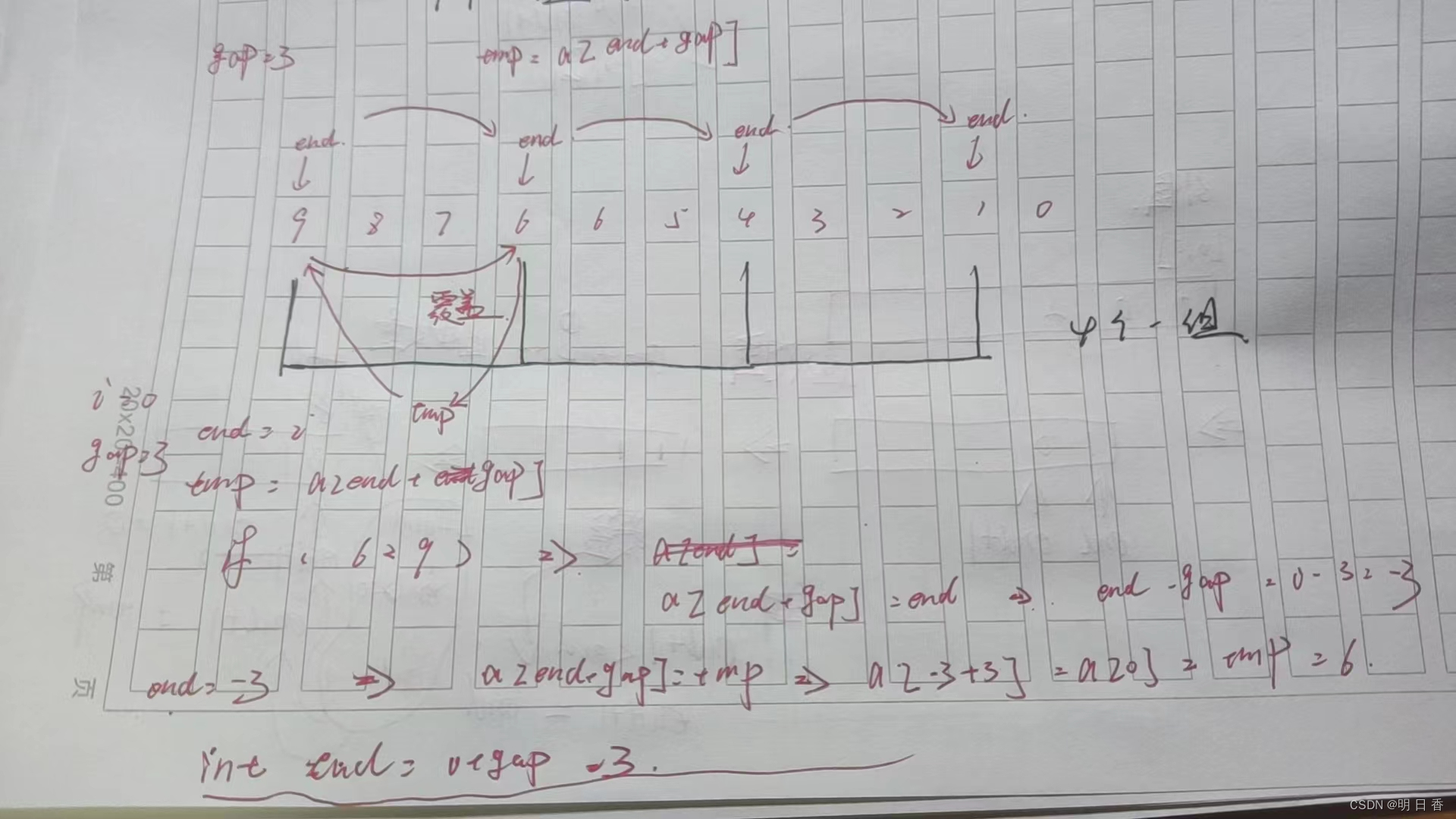
- 如下图所示,每个三个间隙为一组进行直接插入排序。
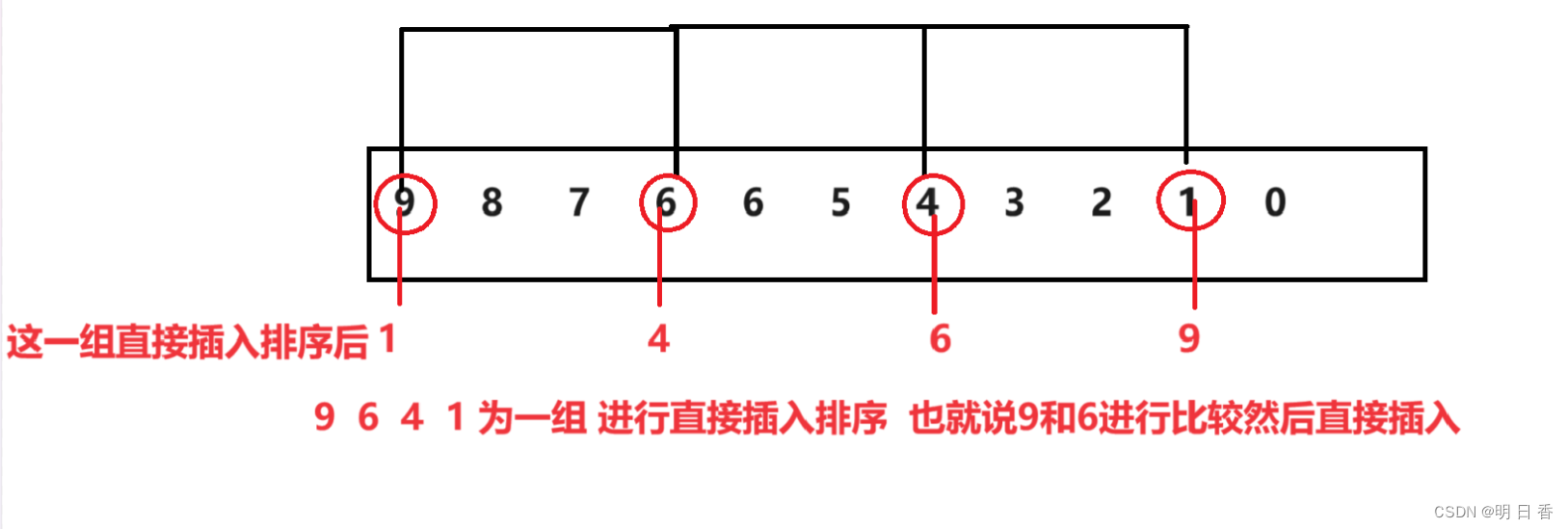
- 当然不止是分为这一组!
代码实现:
预排序:
预排序的内部和直接排序毫无区别,只是进行将数组分为了几组,在组内进行元素的交换
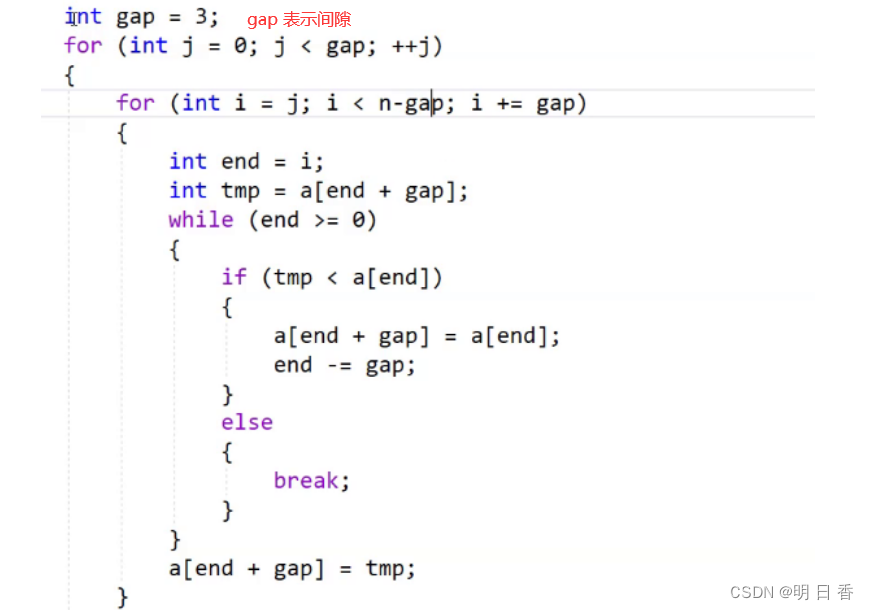
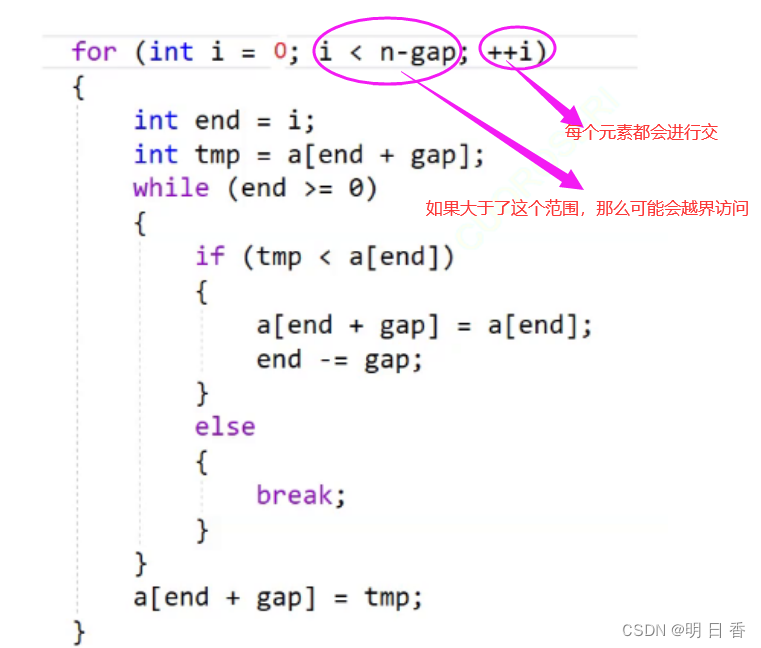
- n-gap :如果大于了这个范围,那么可能会越界访问
- j 表示 组数,总共有gap 组
gap不仅表示间隔几个一组也表示总共分为几组,因为如果每一个元素都和与它相隔gap个间隔的交换判断会有重复的,所以干脆分为gap组,这下将gap组全部内部直接插入排序完后在进行直接插入排序。
简单来说这是一组内的元素全部进行了比较交换后开始第二组,也就是while走完后,进入了外层的for表示开始第二组交换。
代码优化:
如上文所诉,本次的代码可能会出现重复的交换检查,但是这并不会对代码造成任何印象,反倒是对代码起到了简化的作用。
如果上上文讲诉的代码是单独将一组出来交换后换下一组交换,而这一个代码则是一组交换完一对元素后换下一组交换一对元素 。
gap 的 本质 :
- gap越大,大的值更快调到后面,小的值可以更快的调到前面,越不接近有序gap越小,跳得越慢,但是越接近有序。
- 如果gap==1就是直接插入排序。
- 如果 gap > 1 就是预排序
直接插入排序:
因为 n 越大 gap 就必须变大,而gap 变大跳的范围越大,排序也就越不有序,所以导致了gap 这个值的不固定,但是 对于这个问题可以使用多次预排序进行解决。
- 每次预排序结束后将gap的值缩小以此来将整个数组变得接近有序,直到 gap == 1时 完成最后的 希尔排序的 第二步——直接插入排序。

代码图解:
总结:
希尔排序其实就是直接插入排序的升级版本,本质上是将数组中的元素分为多组进行直接排序后,在将整个数组进行直接排序。