当前位置： 首页 > article >正文

图的建立与实现(使用邻接矩阵)(附赠Kruskal算法)

article 2024/11/15 3:37:58

1.创建存储结构

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
#define OVERFLOW 0
#define MAXINT 32767
#define MVNum 100
typedef int Status;
typedef char VerTexType;
typedef int ArcType;

/*静态数组无法销毁7*/
typedef struct {
	VerTexType vexs[MVNum];/*定点*/
	ArcType arcs[MVNum][MVNum];/*矩阵*/
	int vexnum;/*顶点*/
	int	arcnum;/*边*/
}AMGraph;

2.创建一些图的功能(附赠卡鲁斯算法)


Status CreateUDN(AMGraph& G);//创建无向网

Status LocateVex(AMGraph G, VerTexType v);//获取对应元素地址

/*深度优先遍历*/
//============================================================================
void DFSAM(AMGraph G, int index);//遍历对应定点那一行
void DFS_Traveral(AMGraph G, VerTexType v);//从对应定点开始遍历  深度优先遍历
//============================================================================

void PrintfGraphElem(AMGraph G);//打印图元素

/* 下面是实现广度优先遍历  借助队列 或者使用数组*/
//=====================================================//
typedef struct QNode {
	VerTexType data;
	struct QNode* next;
}QNode, * Queptr;
typedef struct {
	Queptr front;//表头
	Queptr rear;//表尾
}LinkQueue;
Status initQueue(LinkQueue& Q);//初始化队列
Status EnQueue(LinkQueue& Q, VerTexType e);//入队
VerTexType DeQueue(LinkQueue& Q);//出队,并获取出队元素
void BFS(AMGraph G, VerTexType v);//从某定点开始广度优先遍历
//======================================================//


/*卡鲁斯卡尔算法  连通图*/
//======================================================//
void Kruskal(AMGraph G);
struct Evode {
	char Head;
	char Tail;
	int lowcost;
}Edge[(MVNum * (MVNum - 1)) / 2];
//======================================================//


Status InsertVex(AMGraph &G, VerTexType v);//向图里面插入v元素
Status InsertArc(AMGraph &G, VerTexType v1,VerTexType v2, int w);//添加边

3.每个函数的具体实现过程

Status CreateUDN(AMGraph& G) {
	//邻接矩阵表示法
	//输入顶点个数和边的个数
	printf("请输入定点个数\n");
	scanf("%d",&G.vexnum);
	getchar();
	printf("请输入边的个数\n");
	scanf("%d", &G.arcnum);
	getchar();

	if (G.arcnum > 0.5 * (G.vexnum * (G.vexnum - 1))) {
		printf("边数输入过多\n");
		return ERROR;
	}
	//初始化定点信息
	printf("请输入%d个定点(回车隔开)\n", G.vexnum);
	for (int i = 0; i < G.vexnum; ++i) {
		scanf("%c", &G.vexs[i]);
		getchar();//吞掉回车或空格
	}

	//初始化矩阵 都为无穷大
	for (int i = 0; i < G.vexnum; ++i) {
		for (int j = 0; j < G.vexnum; ++j) {
			G.arcs[i][j] = MAXINT;//使用Int最大值表示无穷大
		}
	}

	//构造临街矩阵
	char v1;
	char v2;
	int w=0;
	for (int k = 0; k < G.arcnum; ++k) {
		printf("请输入第一个定点\n");
		scanf("%c", &v1);
		getchar();
		printf("请输入第二个定点\n");
		scanf("%c", &v2);
		getchar();
		printf("请输入权值\n");
		scanf("%d",& w);
		getchar();
		int i = LocateVex(G, v1);
		int j = LocateVex(G, v2);
		if (i == -1 || j == -1) {
			printf("不存在该顶点,请重新输入\n");
			--k;
			continue;
		}
		G.arcs[i][j] = w;
		G.arcs[j][i] = w;
	}
	return OK;
}
Status LocateVex(AMGraph G, VerTexType v) {
	for (int i = 0; i < G.vexnum; i++) {
		if (v == G.vexs[i])return i;
	}
	return -1;
}
//标志数组  用来记录是顶点是否被记录
int tempArr[MVNum];
void DFSAM(AMGraph G, int index){//index 表示矩阵的行位置
	printf("%c\t", G.vexs[index]);
	tempArr[index] = 1;

	for (int i = 0; i < G.vexnum; ++i) {
		if (G.arcs[index][i] != MAXINT && tempArr[i] != 1) {
			DFSAM(G, i);
		}
	}

}
void DFS_Traveral(AMGraph G, VerTexType v) {
	//初始化临时辅助数组.
	int indexTemp = LocateVex(G,v);
	if (indexTemp == -1) {
		printf("输入的顶点不存在!\n");
		return;
	}

	for (int i = 0; i < G.vexnum; ++i) {
		tempArr[i] = 0;
	}
	int index = LocateVex(G, v);
	//从指定位置遍历
	for (int i = index; i < G.vexnum; ++i) {	
		if (!tempArr[i]) {
    /*调用遍历函数函数*/
			DFSAM(G, i);
		}
	}
	for (int i = 0; i < index; ++i) {
		if (!tempArr[i]) {
			DFSAM(G, i);
		}
	}
}

void PrintfGraphElem(AMGraph G) {
	printf("元素依次为%c\t\n");
	printf("\t");
	for (int i = 0; i < G.vexnum; ++i) {
		printf("%c\t", G.vexs[i]);
	}
	printf("\n");
	for (int i = 0; i < G.vexnum; ++i) {
		printf("%c\t", G.vexs[i]);
		for (int j = 0; j < G.vexnum; ++ j) {
			if (G.arcs[i][j] == MAXINT)printf("∞\t");
			else printf("%d\t",G.arcs[i][j]);
		}
		printf("\n");
	}
}

Status initQueue(LinkQueue& Q) {
	Q.front = Q.rear = (QNode*)malloc(sizeof(QNode));
	if (Q.front == NULL) exit(OVERFLOW);//申请内存失败结束程序
	Q.front->next = NULL;//初始化
}
Status EnQueue(LinkQueue& Q, VerTexType e) {
	Queptr p = (QNode*)malloc(sizeof(QNode));
	if (!p)exit(OVERFLOW);
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;//连接到之前的表尾
	Q.rear = p;//表尾更新
	return OK;
}
VerTexType DeQueue(LinkQueue& Q) {
	if (Q.front ==Q .rear)return ERROR;//队空
	Queptr p =Q .front->next;//含队头
	VerTexType v = p->data;
	Q.front->next = p->next;
	if (Q.rear == p)Q.rear = Q.front;//当只有一个元素时,即你所删的元素为表尾时
	free(p);
	return v;
}

/*
* 1.从指定定点开始遍历 遍历关联的顶点
* 2.把关联的顶点依次遍历入队,
* 3.依次把队头元素的顶点遍历并入队,然后依次出队
*/
void BFS(AMGraph G, VerTexType v) {
	int index = LocateVex(G, v);
	if (index == -1) {
		printf("输入的顶点不存在!\n");
		return;
	}
	printf("%c\t", v);
	LinkQueue Q;
	Q.front = NULL;
	Q.rear = NULL;
	initQueue(Q);
	int index1 = LocateVex(G, v);
	EnQueue(Q, v);
	//标志数组初始化
	for (int i = 0; i < G.vexnum; ++i) {
		tempArr[i] = 0;
	}
	tempArr[index1] = 1;
	while (Q.front != Q.rear) {

		VerTexType vTemp = DeQueue(Q);
		int index2 = LocateVex(G, vTemp);
		for (int i = 0; i < G.vexnum; ++i) {
			if (tempArr[i] != 1 && G.arcs[index2][i] != MAXINT) {//把要遍历元素对应一行的中的元素且标志数组不为1,的遍历一遍,并入队,然后依次遍历
				printf("%c\t", G.vexs[i]);
				tempArr[i] = 1;
				EnQueue(Q, G.vexs[i]);
			}
		}
	}
	//非联通的打印出来
	for (int i = 0; i < G.vexnum; ++i) {
		if (tempArr[i] != 1) {
			printf("%c\t", G.vexs[i]);
			tempArr[i] = 1;
		}
	}

}
Status InsertVex(AMGraph &G, VerTexType v) {
	if(G.vexnum>=MVNum){
		printf("添加失败,空间已满\n");
		return ERROR;
	}
	G.vexs[G.vexnum] = v;
	for (int i = 0; i < G.vexnum + 1; ++i) {
		G.arcs[G.vexnum][i] = MAXINT;
		G.arcs[i][G.vexnum] = MAXINT;
	}
	G.vexnum++;
	
	return OK;
}
Status InsertArc(AMGraph &G, VerTexType v1, VerTexType v2,int w){
	if (G.arcnum > 0.5 * (G.vexnum * (G.vexnum - 1))) {
		printf("边数已经饱和\n");
		return ERROR;
	}
	//写入关系
	int i = LocateVex(G, v1);
	int j = LocateVex(G, v2);

	if (i == -1 || j == -1) {
		printf("不存在该顶点,请重新输入\n");
		return ERROR;
	}
	G.arcs[i][j] = w;
	G.arcs[j][i] = w;
	return OK;
}
void Kruskal(AMGraph G) {
	int assists[MVNum];
	for (int i = 0; i < G.vexnum; ++i) {
		assists[i] = i;
	}
	//初始化边结构体
	int temp = 0;
	for (int i = 0; i < G.vexnum; ++i) {
		for (int j = 0; j < G.vexnum; ++j) {
			if (G.arcs[i][j] != MAXINT && j > i) {
				Edge[temp].Head = G.vexs[i];
				Edge[temp].Tail = G.vexs[j];
				Edge[temp].lowcost = G.arcs[i][j];
				temp++;
			}
		}
	}
	//对结构体进行排序
	for (int i = 0; i < G.arcnum - 1; ++i) {
		for (int j = i + 1; j < G.arcnum; ++j) {
			if (Edge[j].lowcost < Edge[i].lowcost) {
				Evode temp2 = Edge[i];
				Edge[i] = Edge[j];
				Edge[j] = temp2;
			}
		}
	}
	for (int i = 0; i < G.arcnum; ++i) {
		int v1 = LocateVex(G, Edge[i].Head);
		int v2 = LocateVex(G, Edge[i].Tail);
		int vs1 = assists[v1];
		int vs2 = assists[v2];
		if (vs1 != vs2) {
			printf("%c->%c\n", Edge[i].Head, Edge[i].Tail);
			for (int j = 0; j < G.vexnum; ++j) {
				if (assists[j] == vs2) {
					assists[j] = vs1;
				}
			}
		}
	}
}

int Menu() {
	int choice;
	printf("=======================================================\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<1.创建图>>>>>>>>>>>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<2.深度优先遍历图>>>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<3.广度优先遍历>>>>>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<4.打印图中的元素>>>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<5.向图里添加新顶点>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<6.向图里添加新边>>>>>>>>>>>>>>||\n");
	printf("||<<<<<<<<<<<<<<<7.卡鲁斯卡尔最小生成树(必须是连通图)||\n");
	printf("||<<<<<<<<<<<<<<<<<<<<<8.退出>>>>>>>>>>>>>>>>>>>>>>>>||\n");
	printf("=======================================================\n");
	scanf("%d", &choice);
	getchar();//吞掉回车

	return choice;
}

卡鲁斯算法具体参考我的上一个帖子:PTA 6-5 最小生成树（克鲁斯卡尔算法）-CSDN博客

 4.使用mian主函数把所有函数串用起来

int main(void) {
	AMGraph G;
	G.vexnum = 0;
	G.arcnum = 0;

	int choice;
	int temp;
	char v1 = 0;
	char v2 = 0;
	int w = 0;
	while (true) {
		choice = Menu();
		switch (choice)
		{
		case 1:
			temp = CreateUDN(G);
			if (temp == ERROR)return 1;
			printf("图中元素为:\t\n");
			PrintfGraphElem(G);
			break;

		case 2:	
			if (G.vexnum <= 0 || G.arcnum <= 0) {
				printf("该图为空图\n");
				break;
			}
			char ch;
			printf("请输入你想遍历的起点\n");
			scanf("%c", &ch);
			getchar();
			DFS_Traveral(G, ch);
			printf("\n");
			break;
		case 3:
			if (G.vexnum <= 0 || G.arcnum <= 0) {
				printf("该图为空图\n");
				break;
			}
			printf("请输入你想遍历的起点\n");
			scanf("%c", &ch);
			getchar();
			BFS(G, ch);
			printf("\n");
			break;

		case 4:
			PrintfGraphElem(G);
			break;
		case 5:
			printf("请输入你想插入的节点:(char)\n");
			scanf("%c", &ch);
			getchar();
			temp = InsertVex(G, ch);
			if (temp == OK) printf("添加成功\n");
			break;
		case 6:
			
			printf("请输入第一个定点\n");
			scanf("%c", &v1);
			getchar();
			printf("请输入第二个定点\n");
			scanf("%c", &v2);
			getchar();
			printf("请输入权值\n");
			scanf("%d", &w);
			getchar();
			temp = InsertArc(G, v1, v2, w);
			if (temp == OK)printf("插入成功!\n");
			break;
		case 7:
			Kruskal(G);
			break;
		default:
			exit(OVERFLOW);
		}
	}
    
}

5. 运行界面

我们使用下列图俩创建一个图

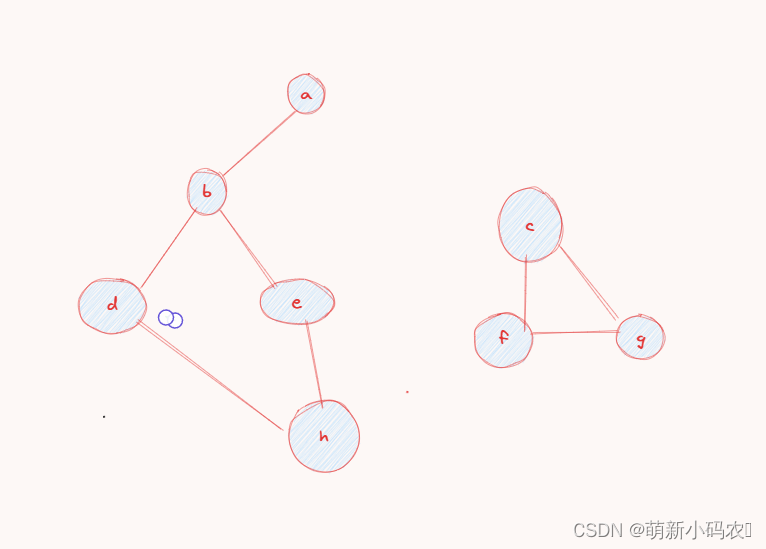
先运行程序

 

然后我们就可以根据界面提示来一步一步创建图了,由于上面没有标明权值,我们就默认为1

 

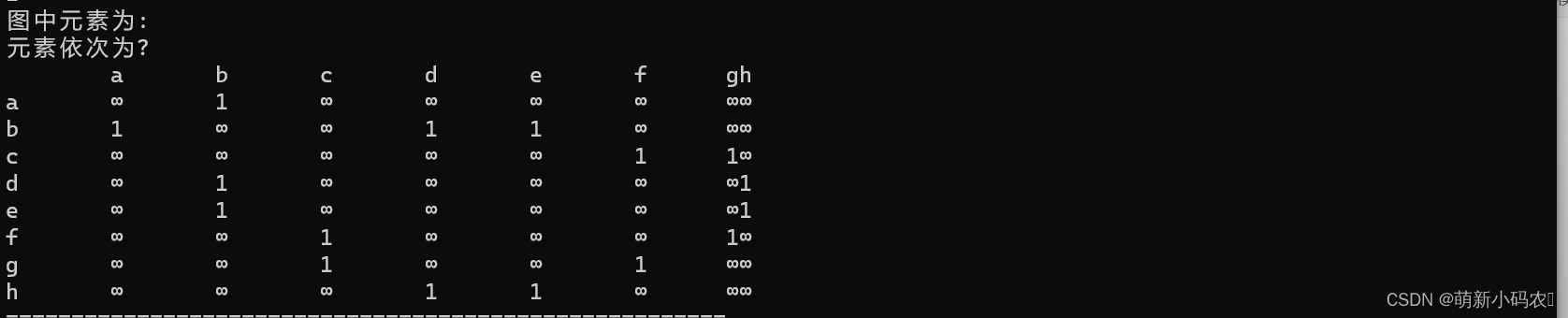
6.总结

以上为图的实现过程,要注意掌握递归的使用和辅助数组的熟练运用 


http://www.kler.cn/a/160148.html

相关文章：

  • A3超级计算机虚拟机，为大型语言模型LLM和AIGC提供强大算力支持
  • Ceph 中PG与PGP的概述
  • JavaWeb后端开发知识储备1
  • 贪心算法day03（最长递增序列问题）
  • ubuntu-desktop-24.04上手指南(更新阿里源、安装ssh、安装chrome、设置固定IP、安装搜狗输入法)
  • Python 连接 Redis 进行增删改查（CRUD）操作
  • 『亚马逊云科技产品测评』活动征文｜ 基于etcd实现服务发现
  • Hello World！
  • TCP连接为什么是三次握手，而不是两次和四次
  • rabbitmq技术
  • 浅析计算机网络安全的的防范与措施
  • java开发中Dao层和Mapper层的关系
  • 微信玩具小程序商城开发技巧
  • 网络安全威胁——跨站脚本攻击
  • 【tower-boot 系列】redis集成
  • docker安装及配置mysql
  • HarmonyOS 修改App的默认加载的界面（ArkTS版本）（十七）
  • [Electron] 将应用打包成供Ubuntu、Debian平台下安装的deb包
  • DAPP开发【11】IPFS星际文件管理系统
  • spark的安装与使用：一键自动安装
  • TCP与UDP的区别
  • HashMap系列-放入元素的流程
  • 面试官问：怎么判断对象已死？
  • 近期复习四
  • 《微信小程序开发从入门到实战》学习四十二
  • 不同数据库进行同步和增量数据（SQL server 与MySQL数据库为例）