当前位置：首页 > article >正文

机器学习应用 | 使用 MATLAB 进行异常检测（上）

article 2024/11/15 4:00:05

异常检测任务，指的是检测偏离期望行为的事件或模式，可以是简单地检测数值型数据中，是否存在远超出正常取值范围的离群值，也可以是借助相对复杂的机器学习算法识别数据中隐藏的异常模式。

在不同行业中，异常检测的典型应用场景包括：

根据设备传感器采集的信号，识别零部件故障类型

自动检测生产线中产品加工异常，降低不良率或辅助质检人员提高工作效率

监控金融交易中是否存在诈骗行为

根据医学影像数据，识别癌组织及其边界

针对异常数据的不同，以及是否可以人为判断异常行为或故障模式，实现方式各有千秋。本文分为上下两篇，在第一部分，将梳理异常检测问题的一般处理思路，第二部分则结合示例重点讨论基于统计和机器学习的无监督异常检测方法。

什么是异常值

异常值包括离群值和奇异值，以下是相关定义：

离群值（outlier）：偏离正常范围的数据，可能是由传感器故障、人为录入错误或异常事件导致，在构建机器学习或统计模型前，如果不对离群值做任何处理，可能会导致模型出现偏差。

奇异值（novelty）：数据集未受到异常值污染，但是存在某些区别于原数据分布的观测数据。

首先，了解你的数据

在一头扎进算法或模型开发之前，首先需要做的是仔细查看手中的数据，并考虑以下问题：

原始数据中的异常是否是显而易见的？

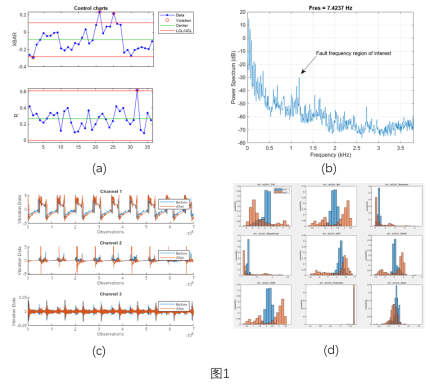
机电设备的停机、堵转等异常现象，从信号波形就可以直接判断异常原因和发生时间，这类问题比较简单，常用突变点检测函数 findchangepts 或过程控制 SPC (Statistical Process Control) 中 control chart 进行处理。例如图 1(a) 中超出上下置信区间的数据点即为异常点，具体可查看示例：Find abrupt changes in signal[1] ，Control Charts[2] ，统计过程控制[3]

从原始数据中是否可以提取出能够有效区分异常的特征？

旋转机械设备的正常和异常数据，从时域信号的波形看上去往往相差无几，但是经过频域变换后，不同频率分量的幅值，可能有较大的不同，这种情况下，可根据频域特征直接检测出异常，如图 1(b) 中标记的异常部分。

从统计分析的角度，是否可以分区异常和正常数据？

Predictive Maintenance Toolbox™ 内置的Diagnostic Feature Designer App，可以帮助我们提取时域和频域特征，并分析其统计分布，例如，在工业设备应用中，利用三轴加速度传感器，分别采集设备维护前（蓝色）和维护后（红色）的振动信号，如图 1(c) 所示，对这两类信号（每类多个样本）提取标准差、斜度等常用统计特征，再分析两类信号的特征直方图，见图 1(d)，不难看出，二者的各个特征的统计分布均存在一定差异。此外，在 Diagnostic Feature Designer App 中，还可以使用一系列特征排序的方法，例如在有标签或无标签的条件下，分别选用 One-Way ANOVA 和 Laplace Score 分析哪些特征可以更好地辅助判断，并利用这些特征作训练基于机器学习的异常检测模型。

如果无法确定数据中是否存在特定的异常模式，应该如何处理？

在全天候运行的工业设备中，故障停机意味着产能的降低，因此设备运营阶段往往采取预防性维护的策略，这意味着异常数据稀缺，并且采集到数据全部或大多是正常数据，异常数据的占比往往较低（获取难度大风险高，或是无法描述异常模式），这也是为什么异常检测任务多被处理为无监督学习问题，仅仅通过正样本（正常数据）训练算法实现任务，或根据数据的隐藏特性筛选出其中的异常样本。

关于如何选择异常检测方法，可参考该链接了解更多相关函数和适用条件：Decision Models for Fault Detection and Diagnosis [4]

简单的一维数据异常检测问题

针对一维数据的异常值检测，处理方法有以下几种：

是否超出历史数据的最大值/最小值

3σ 原则：如果数据符合正态分布，可将 ±3σ 作为极限误差，将落在 μ±3σ 以外样本作为离群值

可以通过箱线图分析/四分位数检验、Grubbs 等方法，进行检测。

例如，针对一组随机生成数，使用 boxchart 函数绘制箱线图，可以简单有效地可视化离群值，默认情况下，boxchart 使用 'o' 符号显示每个离群值。

% 创建一个一维的随机数向量data = randn(1,1000);boxchart(data,"DisplayName","random data")legend% 选取其中一个离群值ax = gca;chart = ax.Children(1);datatip(chart,"1",3.425);

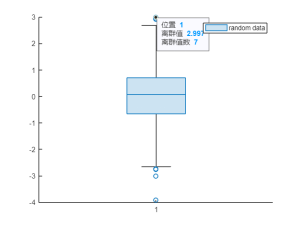
或者使用实时任务“清除离群值”，选择合适的检测方法和清理方法，并对数据分布和离群值进行可视化和处理：

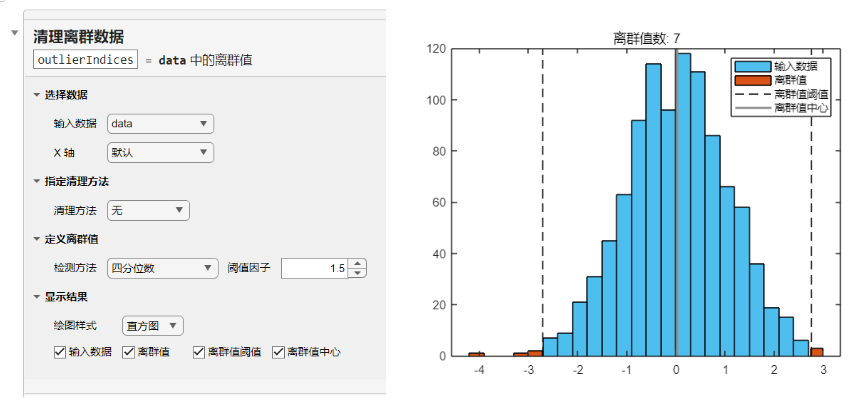
对于多变量（特征）数据集，特征之间可能存在复杂和高度非线性的相关性，上述离群值剔除的方法将不再适用。

高维数据的异常检测

接下来，通过一个基于工业设备振动信号的预测性维护示例，介绍如何着手处理高维数据的异常检测问题，在该例中，原始数据为使用加速度传感器采集的 x/y/z 三个通道的振动信号。在重要工业设备的实际运营过程中，使用者往往采取定期预防性维护的策略，以避免意外停机造成的风险和经济损失，而设备运行一段时间，可能存在一定的零部件磨损和老化问题，这也是导致异常的部分潜在原因，因此样本标签分为两类：“维护前”（before）和“维护后”（after）。

振动信号是典型的时间序列数据，在进行处理时，常用的方法之一是，按设定的时间窗口，对信号进行时域的统计特征提取或频域特征提取，从而转换成以下结构化数据形式：

load("FeatureEntire.mat")head(featureAll)

关于如何进行特征提取，可在命令行窗口运行以下指令，打开对应参考文档查看：

>> openExample('predmaint_deeplearning/AnomalyDetectionUsing3axisVibrationDataExample')

将数据集划分为训练集和测试集：

rng(0) idx = cvpartition(featureAll.label, 'holdout', 0.1);featureTrain = featureAll(idx.training, :);featureTest = featureAll(idx.test, :);

将测试集部分的标签进行替换，将“维护前”（before）定义为“异常”（Anomaly），“维护后”（after）定义为“正常”（Normal）：

trueAnomaliesTest = featureTest.label;trueAnomaliesTest = renamecats(trueAnomaliesTest,["After","Before"], ["Normal","Anomaly"]);featureTestNoLabels = featureTest(:, 2:end);

将训练集中“维护后”（after）的数据样本筛选出来，作为后续异常检测模型的训练样本：

featureNormal = featureTrain(featureTrain.label=='After', :);feat = featureNormal{:,2:end};[NumSamples,Dim] = size(feat)

NumSamples=10282

Dim=12

这个数据集一共有 12 个维度的特征和 10282 条样本。

常用的高维数据可视化方法

为了方便理解数据，可采用以下方法，在低维空间内，对高维数据进行可视化：

1. 通过 plotmatrix 函数，随机抽取 3 个特征，将任意两个特征作为横纵坐标：

plotmatrix(feat(:,randi(size(feat,2),1,3)))title('原始特征')

2. 使用 fsulaplacian 函数，利用 Laplacian Score 算法，选取最重要 2 个特征（第 9 和第 10 个特征）后，绘制其二维平面散点图，观察数据中是否存在某些特定的聚集现象。

idx = fsulaplacian(feat);idx(1),idx(2)

ans=9

ans=10

scatter(feat(:,idx(1)),feat(:,idx(2)),4,'filled')title('基于Laplacian Score选择后的特征')

3. 仅选取其中最重要的特征，可通过 tSNE（t-Distributed Stochastic Neighbor Embedding）对数据进行降维：

rng('default')X=tsne(feat,Standardize=true,Perplexity=100,Exaggeration=20);scatter(X(:,1),X(:,2),4,'filled')title('使用tSNE降维 - 二维')
X3=tsne(feat,Standardize=true,Perplexity=100,Exaggeration=20,NumDimensions=3);scatter3(X3(:,1),X3(:,2),X3(:,3),4,'filled')title('使用tSNE降维 - 三维')

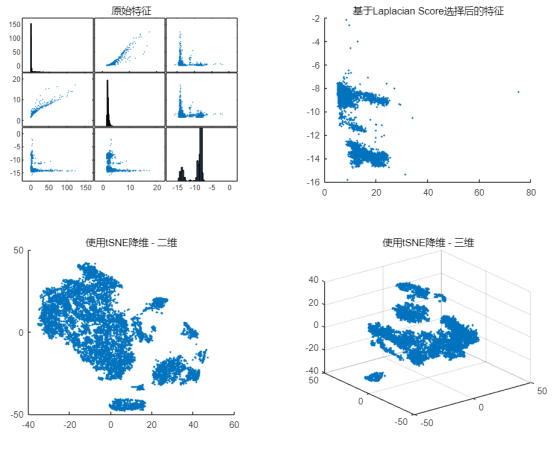
基于 tSNE 进行数据降维的过程中，将融合多个特征得到新的基向量，再将原始数据投射到对应基向量的低维空间进行可视化，在第二部分中，我们将利用这个方法查看训练样本中的异常情况。

有监督异常检测

Statistics and Machine Learning Toolbox™ 提供了基于模型的异常检测算法，如果已将训练数据标注为正常和异常，可以训练二类分类模型，并使用 resubPredict 和 predict 对象函数分别检测训练数据和新数据中的异常。当对设备的全生命周期中的不同状态，例如健康、老化、异常和寿命终末期有足够了解和相关数据标签时，可考虑数据拟合回归模型，或构建聚类模型，以区分不同状态数据。针对上述机器学习模型，以下对象函数常用于检测数据中的异常：

相似度矩阵 — 使用 outlierMeasure[6] 函数计算随机森林 (CompactTreeBagger) 中，样本和其他观测点之间相似度平方值的平均值；

马氏距离 — 使用mahal[7] 函数，适用于判别分析分类模型 (ClassificationDiscriminant) 和高斯混合模型 (gmdistribution)

无条件概率密度 — 使用 logp[8] ，适用于判别分析分类模型 (ClassificationDiscriminant) 和朴素贝叶斯分类模型 (ClassificationNaiveBayes)，包括对应的增量学习模型 (incrementalClassificationNaiveBayes)

此外，利用 Deep Learning Toolbox 构建深度神经网络进行异常检测也是目前该领域的研究热点之一。

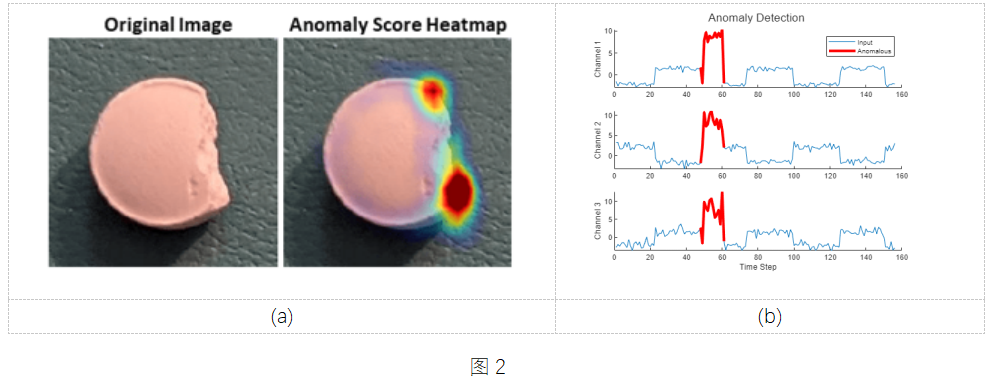
在光学检测领域，如图 2(a) 所示，需要检测图像数据中异常，可构建基于卷积神经网络的图像分类模型，并结合深度学习模型解析的方法，例如类激活映射，对异常区域进行可视化，具体示例可参考：Detect Image Anomalies Using Explainable One-Class Classification Neural Network。[9]

在设备预测性维护应用中，针对传感器信号中的异常检测，多用生成式模型，学习正常数据的特征，并尝试重建数据，再利用重建误差作为判定是否异常的指标，如图 2(b) 所示，例如自编码器AutoEncoder(Time Series Anomaly Detection Using Deep Learning )[10] 和 Graph Deviation Network (Multivariate Time Series Anomaly Detection Using Graph Neural Network) [11] 进行多元时序异常检测。