当前位置：首页 > article >正文

( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】

article 2024/11/15 4:09:34

❓287. 寻找重复数

难度：中等

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 $O (1)$ 的额外空间。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

$1 <= n <= 10^5$
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 $O (n)$ 的解决方案吗？

💡思路：

法一：二分查找

由于数组中存储的数的范围是[1,n]且是连续的，所以我们可以进行二分查找，遍历数组统计小于等于数组中整数范围的中点mid的个数cnt：

如果cnt > mid则重复的数一定在mid左边；
否则一定在mid的右边。
然后区间对半缩小，直到l > h时，l 即为重复的数。

法二：快慢指针

类似于有环链表中找出环的入口：

我们对 nums 数组建图，每个位置 i 连一条 i → nums[i]的边。由于存在的重复的数字 target，因此 target这个位置一定有起码两条指向它的边，因此整张图一定存在环，且我们要找到的 target 就是这个环的入口

对示例1进行建图，如下：

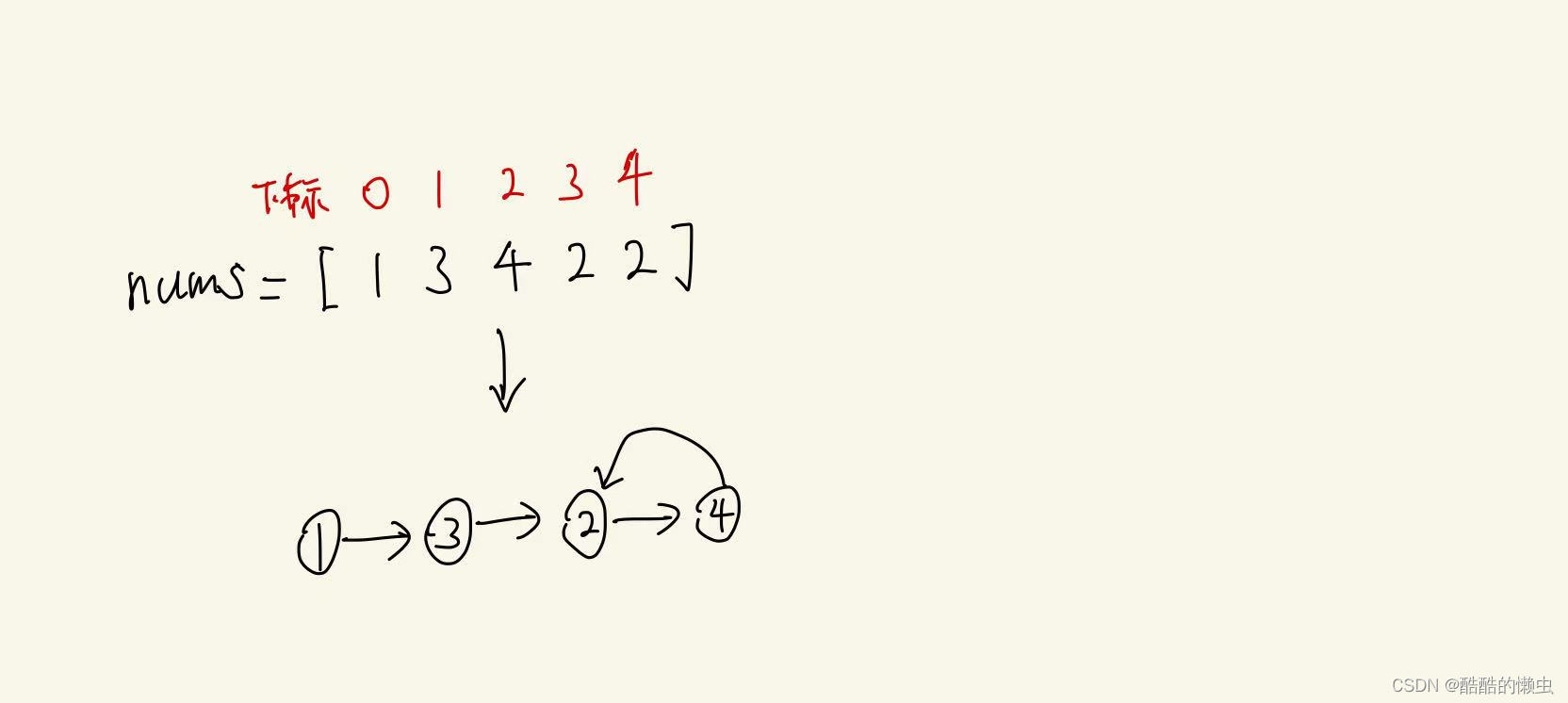
在这里插入图片描述
有两条边指向2，2即是环的入口，也是我们要找的target:

我们先设置慢指针 slow 和快指针 fast ，慢指针每次走一步，快指针每次走两步，根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇;
此时我们再将 slow放置起点 0，两个指针每次同时移动一步，相遇的点就是答案。

这里简单证明为什么后面将 slow 放置起点后移动相遇的点就一定是答案了。
假设环长为L，从起点到环的入口的步数是 a，从环的入口继续走 b 步到达相遇位置，从相遇位置继续走 c 步回到环的入口，则有b＋c= L，其中L、a、b、c都是正整数。

根据上述定义，慢指针走了a＋b步，快指针走了2(a＋b)步。从另一个角度考虑，在相遇位置，快指针比慢指针多走了若干圈，因此快指针走的步数还可以表示成a＋b＋kL，其中 k 表示快指针在环上走的圈数。联立等式，可以得到:
$2 (a + b) = a + b + k L$
解得 a = kL − b，整理可得:
$a = (k - 1) L + (L - b) = (k - 1) L + c$
从上述等式可知，如果慢指针从起点出发，快指针从相遇位置出发，每次两个指针都移动一步，则慢指针走了 a 步之后到达环的入口，快指针在环里走了 k−1 圈之后又走了 c 步，由于从相遇位置继续走 c 步即可回到环的入口，因此快指针也到达环的入口。两个指针在环的入口相遇，相遇点就是答案。

🍁代码：(Java、C++)

法一：二分查找

Java

class Solution {
    public int findDuplicate(int[] nums) {
        int l = 1, h = nums.length - 1;
        while(l <= h){
            int mid = l + (h - l) / 2;
            int cnt = 0;
            for(int num : nums){
                if(num <= mid){
                    cnt++;
                }
            }
            if(cnt > mid) h = mid - 1;
            else l = mid + 1;
        }
        return l;
    }
}

C++

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int l = 1, h = nums.size() - 1;
        while(l <= h){
            int mid = l + (h - l) / 2;
            int cnt = 0;
            for(int num : nums){
                if(num <= mid){
                    cnt++;
                }
            }
            if(cnt > mid) h = mid - 1;
            else l = mid + 1;
        }
        return l;
    }
};

法二：快慢指针

Java

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = nums[0], fast = nums[nums[0]];
        while(slow != fast){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        slow = 0;
        while(slow != fast){
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

C++

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = nums[0], fast = nums[nums[0]];
        while(slow != fast){
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        slow = 0;
        while(slow != fast){
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (n)$ ，其中 n 为 $n u m s$ 数组的长度,「Floyd 判圈算法」时间复杂度为线性的时间复杂度；二分查找时间复杂度为 $O (n l o g n)$ , 二分查找最多需要二分 $O (l o g n)$ 。
空间复杂度： $O (1)$ ，我们只需要常数空间存放若干变量。