当前位置： 首页 > article >正文

数据结构（六）—— 二叉树（6）二叉搜索树

article 2024/11/15 22:55:18

文章目录

  • 题
  • 1 700 二叉搜索树中搜索指定元素
    • 开塞递归
    • 递归2（利用二叉搜索树）
    • 递归3(bj)
    • 迭代
  • 2 98 验证二叉搜索树
  • 3 530 二叉搜索树的最小绝对差
    • 递归中序遍历转化为数组
    • 递归
  • 4 501 二叉搜索树中的众数
    • 额外的内存开销（哈希表）
    • 无额外内存开销，重复利用二叉搜索数中众数相邻的特点
  • 5 701 二叉搜索树中的插入操作
    • 递归
    • 迭代
  • 6 108 将有序数组转换为二叉搜索树
  • 中等题
  • 1 450 删除二叉搜索树中的节点
  • 2 669 修剪二叉搜索树

题

1 700 二叉搜索树中搜索指定元素

开塞递归

我并没有用到二叉搜索树这个前提
1、输入输出TreeNode* searchBST(TreeNode* root, int val)
2、退出：遍历到空或者满足输入的int则退出
if(root == nullptr || root->val == val) return root;
3、层级逻辑

TreeNode* temp;
temp = searchBST(root->left, val);
if(temp == nullptr){
	temp = searchBST(root->right, val); 
	return temp;
}
return temp;

其中的if的逻辑为：如果没有在左子树上搜索得到能用的TreeNode再搜右子树

4、整合

TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr || root->val == val) return root;

        TreeNode* temp;
        temp = searchBST(root->left, val);
        if(temp == nullptr){
            temp = searchBST(root->right, val); 
            return temp;
        }
        return temp;
}

递归2（利用二叉搜索树）

TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        TreeNode* result = NULL;
        if (root->val > val) result = searchBST(root->left, val);
        if (root->val < val) result = searchBST(root->right, val);
        return result;
}

递归3(bj)

不算遍历了整颗搜索树

class Solution {
public:
    TreeNode* temp = NULL;

    void bfs(TreeNode* root, int val){
        if(root == nullptr ||temp != nullptr) return;

        if(root->val == val) temp = root;
        bfs(root->left, val);
        bfs(root->right, val);
        return;
    }
    
    TreeNode* searchBST(TreeNode* root, int val) {
        bfs(root, val);
        return temp;
    }
};

迭代

充分利用二叉搜索树特性，左小于中、右大于中

TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return NULL;
}

2 98 验证二叉搜索树

中序遍历下，输出的二叉搜索树节点的数值是有序序列。所以可以利用递归中序遍历将二叉搜索树转变成一个数组

class Solution {
public:
    void trans(TreeNode* root, vector<int>& vec){
        if(root == nullptr) return;
        trans(root->left, vec); 
        vec.push_back(root->val);
        trans(root->right, vec); 
        return;
    }
    bool isValidBST(TreeNode* root) {
        vector<int> vec;
        trans(root, vec);
        for(int i = 0; i < vec.size() - 1; ++i){
            if(vec[i+1] <= vec[i]) return false;
        }
        return true;
    }
};

3 530 二叉搜索树的最小绝对差

递归中序遍历转化为数组

与2一样，可以转化为vector，然后相邻元素相减，保存最小的减数

class Solution {
public:
    void trans(TreeNode* root, vector<int>& vec){
        if(root == nullptr) return;
        trans(root->left, vec); 
        vec.push_back(root->val);
        trans(root->right, vec); 
        return;
    }
    int getMinimumDifference(TreeNode* root) {
        int res = INT_MAX;
        vector<int> vec;
        trans(root, vec);
        for(int i = 0; i < vec.size() - 1; ++i){
            res = min(res, vec[i+1] - vec[i]);
        }
        return res;
    }
};

递归

核心技巧：递归中记录前一个节点的指针

trans(root->left, res);   // 左
if(pre != nullptr) res = min(res, root->val - pre->val);   // 中
pre = root; // 记录前一个
trans(root->right, res);   // 右

class Solution {
public:
    TreeNode* pre = NULL;

    void trans(TreeNode* root, int& res){
        if(root == nullptr) return;

        trans(root->left, res);
        if(pre != nullptr) res = min(res, root->val - pre->val);
        pre = root; // 记录前一个
        trans(root->right, res);
        
    }

    int getMinimumDifference(TreeNode* root) {
        int res = INT_MAX;
        trans(root, res);

        return res;
    }
};

4 501 二叉搜索树中的众数

额外的内存开销（哈希表）

class Solution {
public:
    void trans(TreeNode* root, unordered_map<int,int>& visit) {
        if(root == nullptr) return;

        trans(root->left, visit);
        visit[root->val]++;
        trans(root->right, visit);
    }

    vector<int> findMode(TreeNode* root) {
        vector<int> res;
        unordered_map<int,int> visit;
        int fre = INT_MIN;

        trans(root, visit);
        for(auto [a,b] : visit){
            fre = max(fre, b);
        }
        for(auto [a,b] : visit){
            if(b == fre) res.push_back(a);
        }

        return res;
    }
};

复习：遍历哈希表的两种方式

for (auto it = visited.begin(); it != visited.end(); ++it){
	it->first  // key
	it->second   // val
}
或
for(auto [a,b] : visited){
	a   // key
	b   // val
}

哈希映射

for (auto it = visited.begin(); it != visited.end(); ++it)
	*it  // val

无额外内存开销，重复利用二叉搜索数中众数相邻的特点

二叉搜索数中相同元素一定相邻
1、递归函数为dfs
2、逻辑处理在update函数中

class Solution {
public:
    vector<int> answer;
    int base, count, maxCount;

    void update(int x) {
        if (x == base) {
            ++count;
        } else {
            count = 1;
            base = x;
        }
        if (count == maxCount) {
            answer.push_back(base);
        }
        if (count > maxCount) {
            maxCount = count;
            answer = vector<int> {base};
        }
    }

    void dfs(TreeNode* o) {
        if (!o) {
            return;
        }
        dfs(o->left);
        update(o->val);
        dfs(o->right);
    }

    vector<int> findMode(TreeNode* root) {
        dfs(root);
        return answer;
    }
};

5 701 二叉搜索树中的插入操作

插入题
返回值为树的题，还有617合并二叉树，在二叉树（5）中。
这道题根本不用重构，只需要找到合适的空节点位置插入就好了。

递归

1、输入输出
TreeNode* insertIntoBST(TreeNode* root, int val)
2、退出条件
遍历到了合适的空节点

if (root == NULL) {
	TreeNode* node = new TreeNode(val);
	return node;
}

3、单层逻辑
这是搜索树，遍历整棵搜索树简直是对搜索树的侮辱

if (root->val > val)
	root->left = insertIntoBST(root->left, val);
if (root->val < val)
	root->right = insertIntoBST(root->right, val);
return root;

4、整合

TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        
        if (root->val > val) 
        	root->left = insertIntoBST(root->left, val);
        if (root->val < val) 
        	root->right = insertIntoBST(root->right, val);
        return root;
}

补充：需要了解此题与 617合并二叉树 的区别
问题：
为什么不能像617那样新创建一个节点？如下所示：

TreeNode* newNode = new TreeNode(root->val);
if (root->val > val)
	newNode->left = insertIntoBST(root->left, val);
if (root->val < val)
	newNode->right = insertIntoBST(root->right, val);
return newNode;

这样会有问题，他会返回所添加元素5的最短路径，如下所示：
示例：
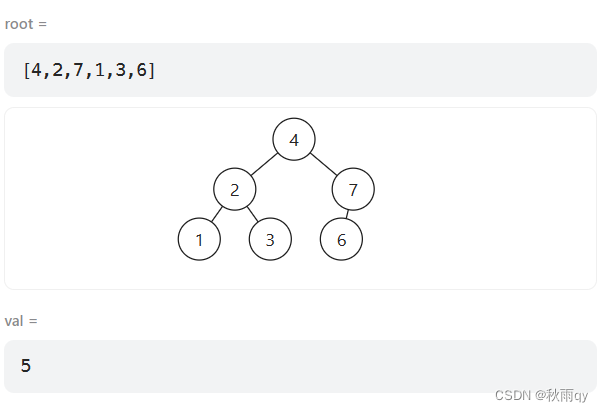
在这里插入图片描述
错误答案：
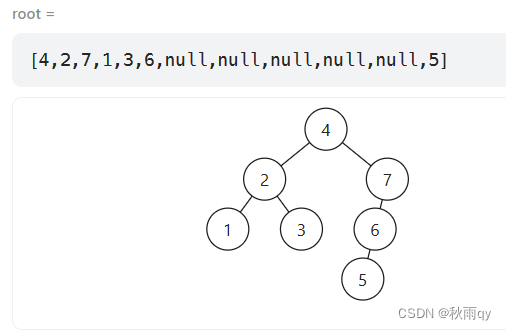
在这里插入图片描述
本应该是：
在这里插入图片描述

迭代

TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* cur = root;
        TreeNode* parent = root; // 这个很重要，需要记录上一个节点，否则无法赋值新节点
        while (cur != NULL) {
            parent = cur;
            if (cur->val > val) cur = cur->left;
            else cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if (val < parent->val) parent->left = node;// 此时是用parent节点的进行赋值
        else parent->right = node;
        return root;
}

6 108 将有序数组转换为二叉搜索树

删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成，这样是比较方便的。

首先是传入数组，然后就是左下标left和右下标right，我们在二叉树：构造二叉树登场！ (opens new window)中提过，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组。
1、输入输出
TreeNode* traversal(vector<int>& nums, int left, int right) {
这里注意，这里定义的是左闭右闭区间，在不断分割的过程中，也会坚持左闭右闭的区间，这又涉及循环不变量。
在106.从中序与后序遍历序列构造二叉树，35.搜索插入位置 和 59.螺旋矩阵II 都详细讲过循环不变量。
2、退出条件
if (left > right) return nullptr;
3、单层逻辑
1 首先取数组中间元素的位置，不难写出int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法 中尤其需要注意！所以最好这么写：int mid = left + ((right - left) / 2);

2 取了中间位置，就开始以中间位置的元素构造节点，TreeNode* root = new TreeNode(nums[mid]);

3 接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点。

4 最后返回root节点，单层递归整体代码如下：

int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;

中等题

1 450 删除二叉搜索树中的节点

删除题
不可避免的要调整树的结构

1、如果删的节点是叶子节点==不需要调整树的结构
2、

2 669 修剪二叉搜索树


http://www.kler.cn/a/17572.html

相关文章：

  • Wireshark中的length栏位
  • Python的Matplotlib
  • 【C#设计模式(4)——构建者模式(Builder Pattern)】
  • 初级数据结构——栈
  • 用MVVM设计模式提升WPF开发体验：分层架构与绑定实例解析
  • Linux系统编程多线程之条件变量和信号量讲解
  • 【redis】spring-cache使用指南
  • 给孩子描述非对称加密算法
  • 代码随想录算法训练营第三十天 | 航班问题、二维回溯
  • HashMap底层结构和源码分析
  • 爬取景区源码
  • 【Maven笔记1】Maven介绍
  • ConcurrentHashMap底层实现原理
  • Java时间类（四）-- DateTimeFormatter类
  • PostgreSQL 基础知识：psql 入门
  • ChatGPT诞生的新岗位：提示工程师（Prompt Engineer）
  • 发展文旅夜游项目有哪些好处
  • Python实现哈里斯鹰优化算法(HHO)优化随机森林分类模型(RandomForestClassifier算法)项目实战
  • 章节3：02-Apache Commons Collections反序列化漏洞
  • 宝塔windows面板提权获取系统管理员权限方法！（非漏洞BUG）
  • JavaEE阶段测试复习
  • 京东数据分析：2023年Q1白酒电商整体动销增长，中低端酒企压力大
  • 国民技术N32G430开发笔记（14）-IAP升级 usart2接收数据
  • MySQL知识学习03（三大日志详解 binlog、redo log、undo log）
  • Python3 简介
  • Android 9.0 系统systemui下拉通知栏的通知布局相关源码分析