当前位置：首页 > article >正文

量子计算（10）量子算法2：Deutsch-Jozsa算法

article 2024/12/25 9:04:11

又到了一周一篇的量子计算啦！全体起立respect！

前言：本篇文章研究的算法，相当无聊。在日常生活中基本上用不到，但是这个算法却能显著的体现出量子计算算法比经典算法更加快速这一特点。这个算法就好比C语言里的hello world、人工智能里的数字图像识别，亦或者代表植物大战僵尸里的旗帜僵尸。并不代表着Deutsch-Jozsa算法多么有用，只是代表恭喜你，你入了量子计算的门了！

1、单变量平衡函数与常函数

2、Deustch算法思想步骤

1、单变量平衡函数与常函数

对于单变量函数f{0,1} $\rightarrow$ {0,1}，即变量与因变量均只能为0或者1的函数。我们把具有以下类型真值表的函数，称之为常函数：

x	f1（x）
0	0
1	0

或者：

x	f2（x）
0	1
1	1

即不管输入怎么样，输出只能全为1或者全为0的函数为常函数。它要么善良的很纯粹，要么坏的很纯粹。

我们把具有以下类型的真值表的函数，称为平衡函数：

x	f3（x）
0	0
1	1

或者：

x	f4（x）
0	1
1	0

即输出里面有一半是1有一半是0，是一个亦正亦邪的存在。

对于经典算法来说，我们需要两次测试，才能得出，这是一个怎样的函数。但是，量子计算就特别强，它只需要一次测试，就能得出来。欲知如何操作，请看下文：

2、Deustch算法思想步骤

还记得上篇文章，我们说过，量子计算里面的变换都是酉变换，是一个可逆电路，对平衡函数，显然满足，但是对于常函数，我们必须进行改造。考考大家，如何对此函数进行改造？

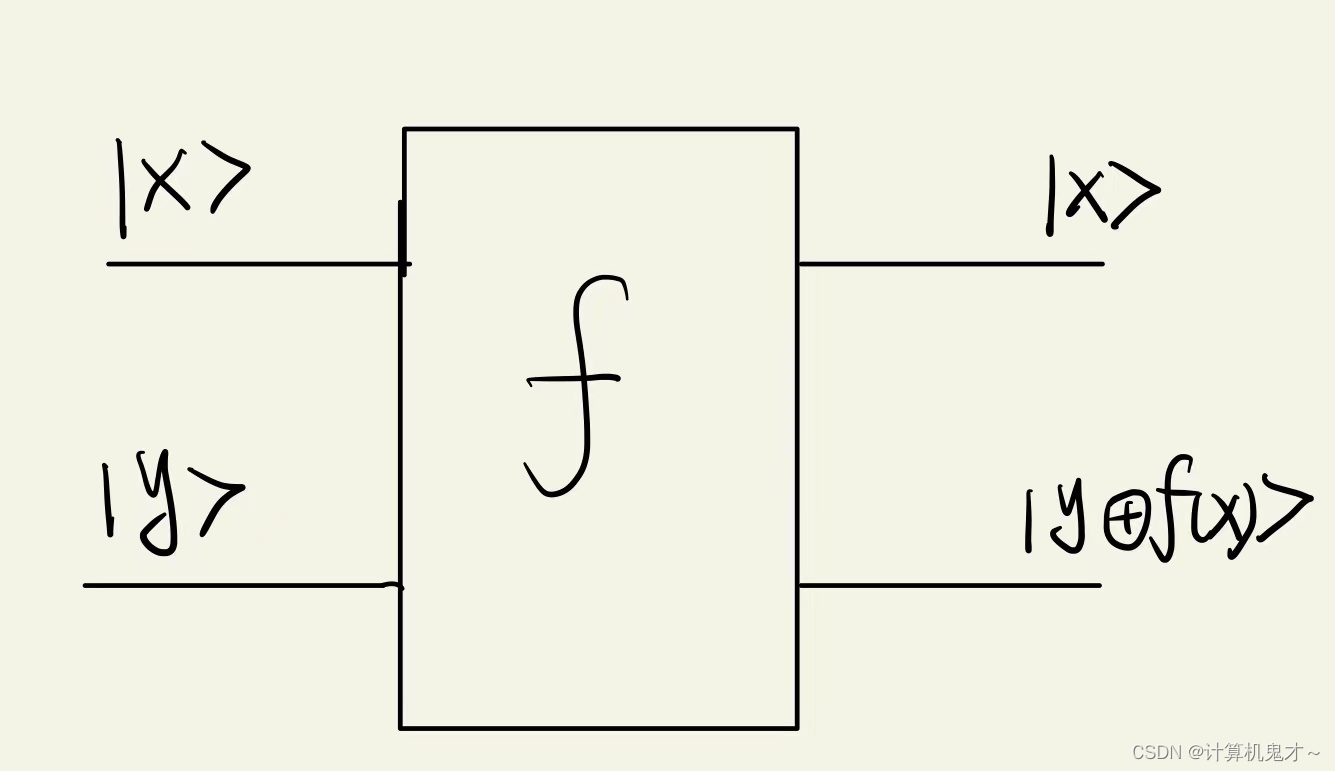
答案如上图，怎么样，有没有想到呢？由这部分电路一起构成下文的Uf，我们令F=y $\oplus$ f（x），我们还是列一个真值表：

x	y	x，F1（x）	x，F2（x）	x，F3（x）	x，F4（x）
0	0	00	01	00	01
0	1	01	00	01	00
1	0	10	11	11	10
1	1	11	10	10	11

满足可逆性！

我们想要一次就能检测出来，说明我们的输入必然为一个叠加态（有|0>也有|1>），那么我们很容易想到H门。至于输出结果的辅助位，暂时还不清楚到底要怎么设计，暂且就让它为|0>态吧。

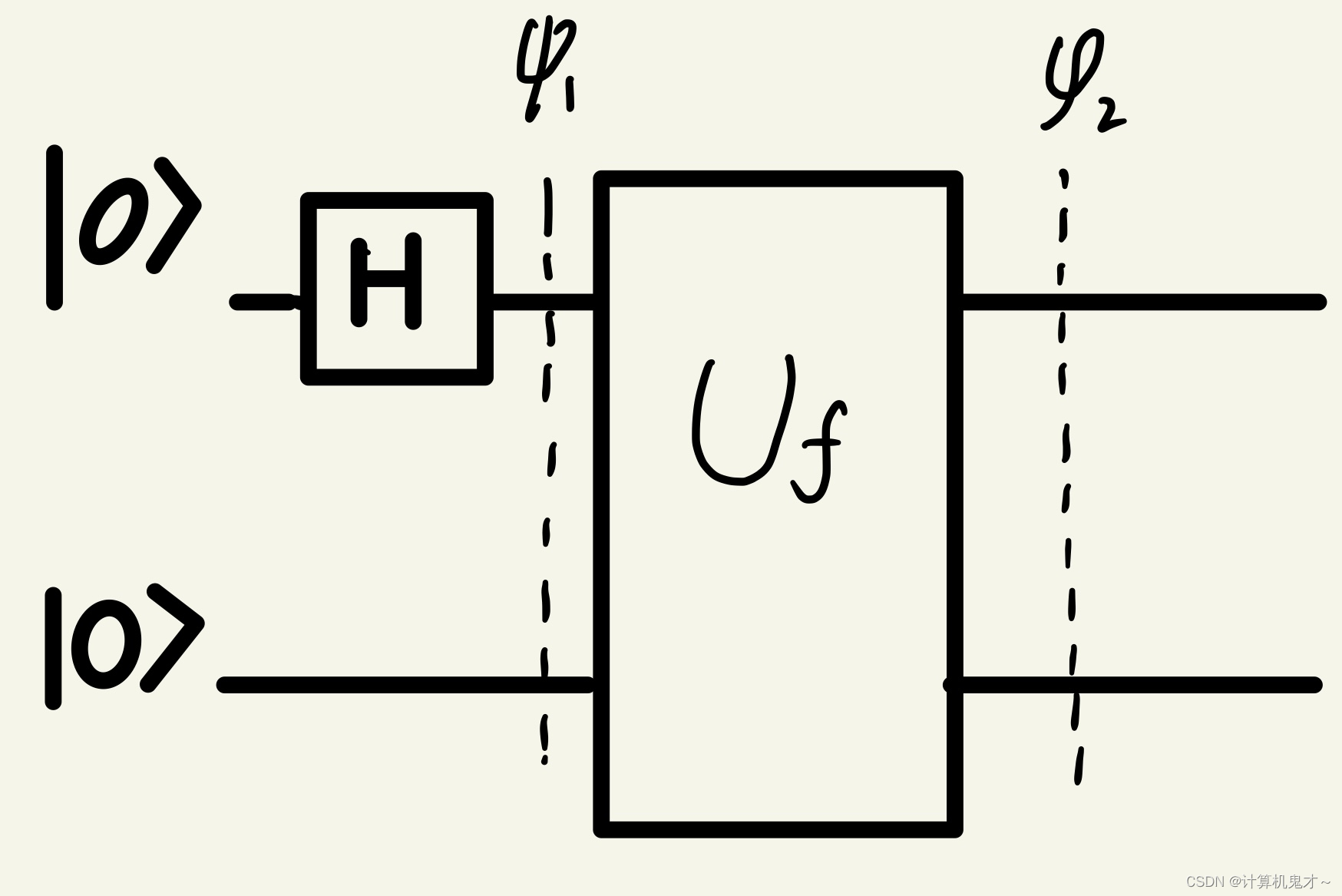
所以我们暂时能得到上面这张图。我们逐步分析一下 $\psi _{1}$ 与 $\psi _{2}$ 的状态。容易知道 $\psi _{1}$ 状态下，量子态为 $\frac{ |00>+|01>}{\sqrt{2}}$ ，而 $\psi _{2}$ 态为 $\frac{|F(0)0>+|F(1)1>}{\sqrt{2}}$ 。

这个时候就有读者会说：“好嘛，亏我还这么相信小编，小编的这波操作下来，让我一脸懵逼，这有啥区别啊？还不是判断不出来平衡函数与常函数？”

欸？此言差矣？至少我们踏出来了正确的一步。我们仔细想想，之所以没有差别，原因在于什么？显然是在于我们没有修改的|0>态啊。但是，如果只改为|1>态，照样一点用都没有，会与|0>态时一样，没有意义。于是，我们仍然选择用一个叠加态，加一个H门，看看对解决问题有没有帮助。

而且我们也知道，两个H门加在一起，就会变成一根线：啥也不是。于是我们再添加一个H门，把电路的量子态变简单一点。

改造的结果如上图，我们还是分析三个位置的量子态。

位置	量子态
$\psi _{1}$	$\frac{\|0>+\|1>}{\sqrt{2}} \otimes \frac{\|0>+\|1>}{\sqrt{2}}$
$\psi _{2}$	$\frac{\|0\oplus f(x)>+\|1\oplus f(x)>}{\sqrt{2}} \otimes \frac{\|0>+\|1>}{\sqrt{2}}$
$\psi _{3}$	$\frac{\|f(x)>+\|\overline{f(x)}>}{\sqrt{2}} \otimes \|0>$

其中x为0或者1，如此一来，确实能产生差别，当为常函数的时候，高位为|+>态，而为平衡函数的时候高位为一个纯态，可以通过检测高位|0>与|1>的百分比，就能知道这到底是什么函数。（常函数各为50%，平衡函数二者中一个为100%另一个为0%）。

虽然我们已经能够判断出来了，但这还不是真正的Deutsch算法，真正的Deutsch算法电路如下图，仅仅只有|0>与|1>之差：

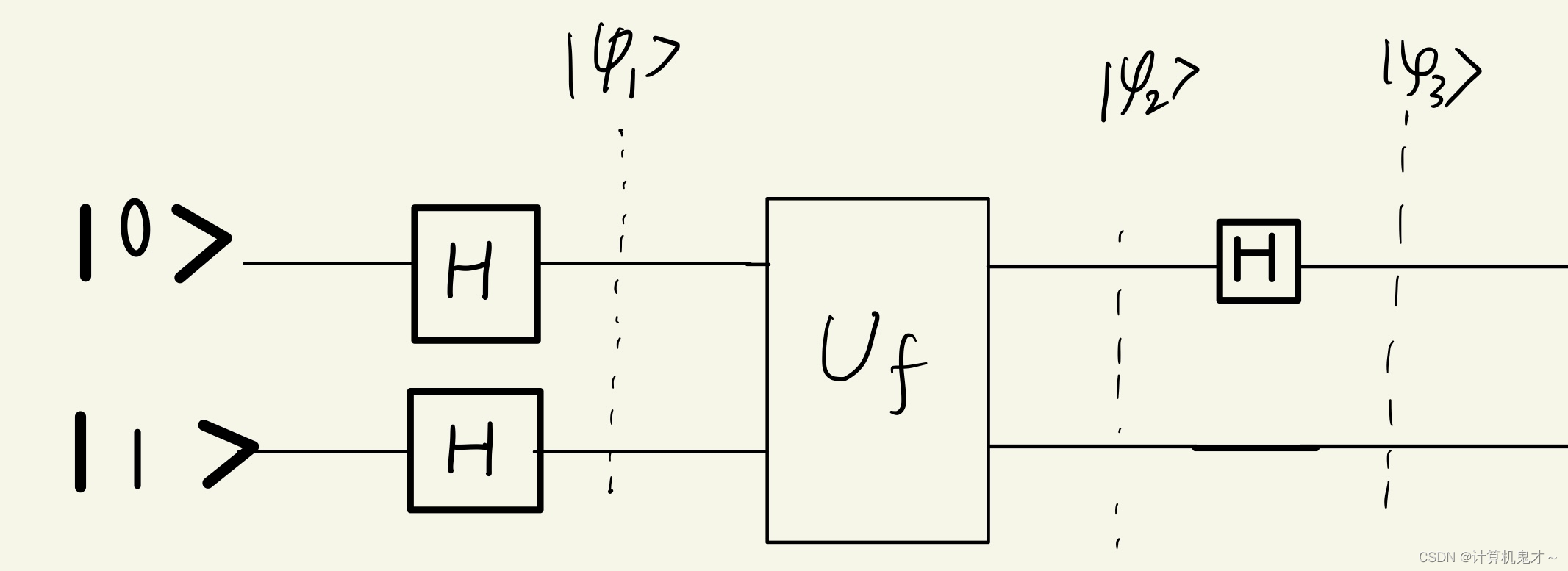
但是这个改变却能让算法更快，请大家仔细观察下面这个式子，最后一步进行规整。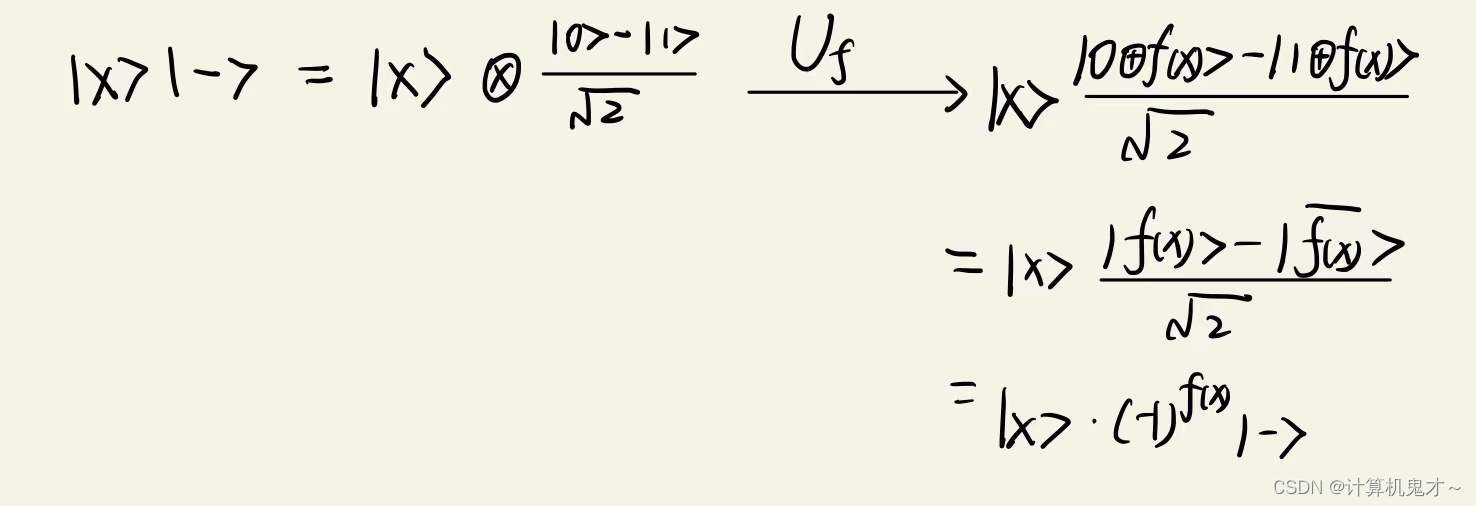

我们分别分析一下 $\psi _{1}$ 、 $\psi _{2}$ 以及 $\psi _{3}$ 的状态：

位置	状态
$\psi _{1}$	$\frac{\|0>-\|1>}{\sqrt{2}}\otimes \frac{\|0>+\|1>}{\sqrt{2}}$
$\psi _{2}$	自己算，见下面的分析
$\psi _{3}$	自己算

最后的差别，就体现在了这一个0与1上边。在 $\psi _{2}$ 状态下，如果低位为|0>，那么高位为 $\frac{|f(0)>-|\overline{f(0)}>}{\sqrt{2}}$ ；如果低位为|1>，那么高位为 $\frac{|f(1)>-|\overline{f(1)}>}{\sqrt{2}}$ 。如果为常函数的话，低位|0>时高位为 $(-1)^{f(0)}|\, ->$ ，低位为|1>时高位为 $(-1)^{f(1)}|\, ->$ ，综合一下，状态为 $\frac{|0>-|1>}{\sqrt{2}} \otimes \frac{|0>+|1>}{\sqrt{2}}$ ，如果为平衡函数的话状态为 $\frac{|0>-|1>}{\sqrt{2}} \otimes \frac{|0>-|1>}{\sqrt{2}}$ ，到 $\psi _{3}$ 位置时，低位的 $\frac{|0>+|1>}{\sqrt{2}}$ 又会转化为|0>态，而 $\frac{|0>-|1>}{\sqrt{2}}$ 会转化为|1>态差异就会产生在低位。