2023美赛C题【分析思路+代码】
以下内容为我个人的想法与实现,不代表任何其他人。
文章目录
- 问题一
- 数据预处理
- 时间序列模型
- 创建预测区间
- 单词的任何属性是否影响报告的百分比?如果是,如何影响?如果不是,为什么不是?
- 问题二
- 问题三
- 难度评估
- 模型简历与预测
- 问题四分类分析
问题一
为了对报告结果数量的变化进行建模,我们需要确定影响这种变化的潜在因素。可能影响报告结果数量的几个可能因素包括:
数据预处理
读取适当修整的数据集:
import pandas as pd
data=pd.read_excel('Problem_C.xlsx')
data
# 日期 比赛编号 单词 报告结果数量 困难模式中的数量 尝试次数
如下:
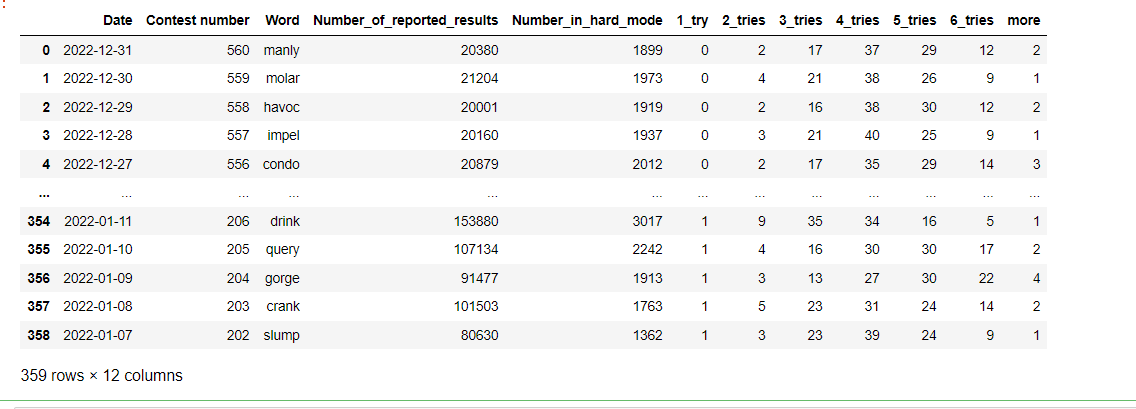
查看数据集的基本信息
# 查看数据集的基本信息
print(data.info())
# 可见没有缺失值
如下:
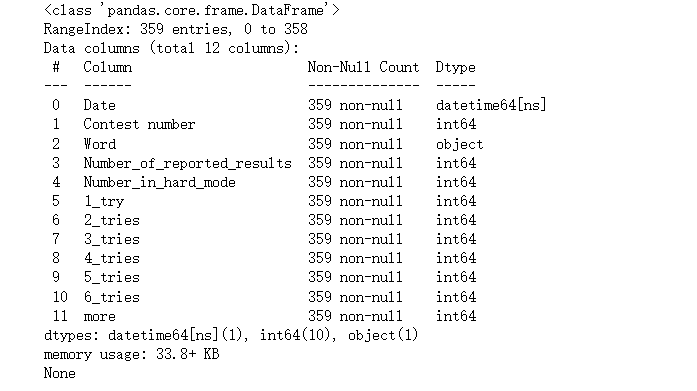
由于同一个日期可能有多条数据,所以统计每个日期的报告结果数量:
# 统计每个日期的报告结果数量
results_by_date = data.groupby('Date')['Number_of_reported_results'].sum()
print(results_by_date)
如下:

统计每个单词的平均猜测次数:
# 统计每个单词的平均猜测次数
avg_guesses_by_word = data[['Word', '1_try', '2_tries', '3_tries', '4_tries', '5_tries', '6_tries', 'more']].mean(axis=1)
print(avg_guesses_by_word)
如下(可见差不多):

检查单词长度是否与平均猜测次数有关:
# 检查单词长度是否与平均猜测次数有关
data['Word length'] = data['Word'].apply(len)
avg_guesses_by_word_length = data.groupby('Word length')[['1_try', '2_tries', '3_tries', '4_tries', '5_tries', '6_tries', 'more']].mean()
avg_guesses_by_word_length
# 说明还是有关系
如下(结果可以看出是有关系的):
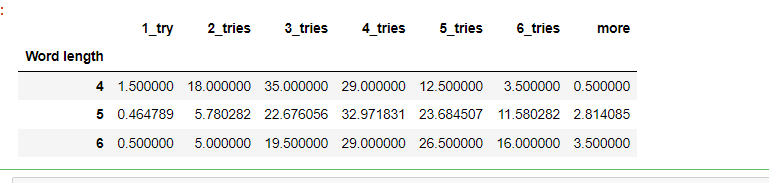
下面做个热力图看看上述特征之间关系:
corr=avg_guesses_by_word_length.corr()
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
plt.subplots(figsize = (10,10))
plt.title("Pearson correlation with label")
sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Oranges")
如下:
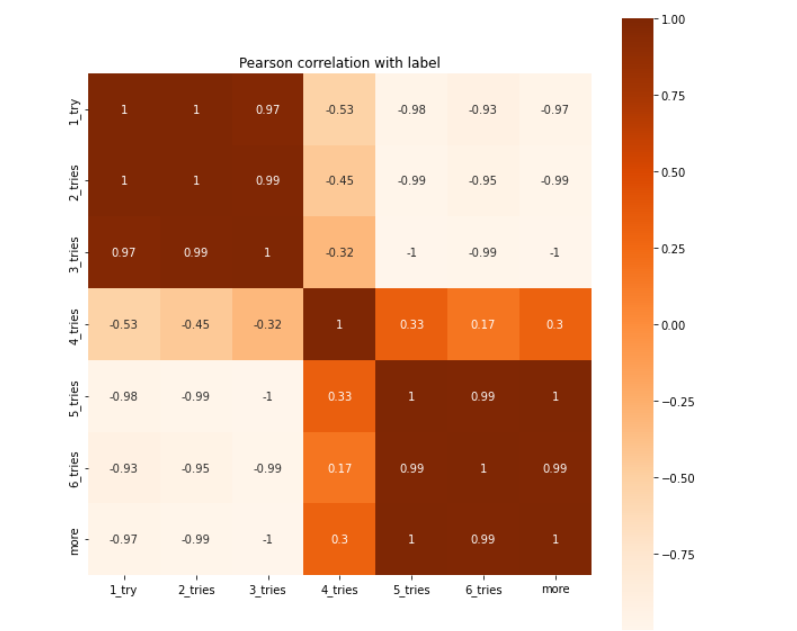
可视化每天报告数量:
# 可视化每天报告数量
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 提取每天的报告结果数量
results_by_date = data.groupby('Date')['Number_in_hard_mode'].sum()
# 绘制时间序列图
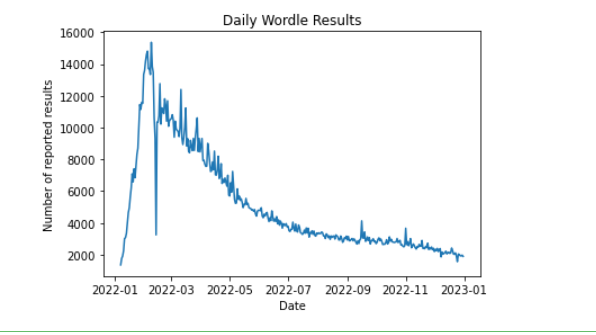
plt.plot(results_by_date)
plt.title('Daily Wordle Results')
plt.xlabel('Date')
plt.ylabel('Number of reported results')
plt.show()
如下:
时间序列模型
ARIMA时间序列模型如下:
# 拆分数据集为训练集和测试集
train, test = train_test_split(results_by_date, test_size=0.2, shuffle=False)
# 建立ARIMA模型并训练
model = ARIMA(train, order=(3, 1, 1))
model_fit = model.fit()
# 对测试集进行预测并计算误差
history = [x for x in train]
predictions = list()
for t in range(len(test)):
model = ARIMA(history, order=(3, 1, 1))
model_fit = model.fit()
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test.iloc[t]
history.append(obs)
RMSE_test = np.sqrt(mean_squared_error(test, predictions))
print("Test RMSE: {}".format(RMSE_test))
# 绘制预测结果和实际结果的比较图
plt.plot(test.index, test.values, label='Actual')
plt.plot(test.index, predictions, label='Predicted')
plt.title('Daily Wordle Results')
plt.xlabel('Date')
plt.ylabel('Number of reported results')
plt.legend()
plt.show()
运行如下:
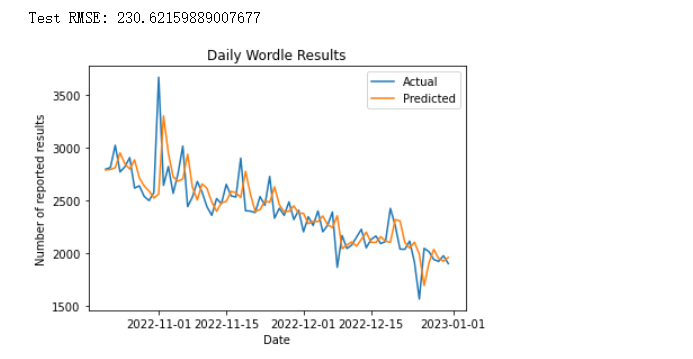
我们计算每天的报告结果数量,并绘制时间序列图来检查数据是否具有某种趋势或周期性。接下来,我们将数据集拆分为训练集和测试集,并建立一个ARIMA模型来训练数据集。在训练模型后,我们对测试集进行预测并计算误差,然后绘制预测结果和实际结果的比较图来评估模型的性能。从上图可以看出,我们的模型表现已经很好。
创建预测区间
2023年3月1日报告的结果数量创建预测区间。首先预测当天值:
import matplotlib.pyplot as plt
# 对未来数据进行预测
forecast = model_fit.forecast(steps=30)
# 提取2023年3月1日的预测值和置信区间
forecast_value = forecast[0]
# 打印预测值
print('2023年3月1日的预测值为:%.2f' % forecast_value)
如下:
2023年3月1日的预测值为:1956.95
均方误差MSE通过计算预测值和实际值之间距离(即误差)的平方来衡量模型优劣。即预测值和真实值越接近,两者的均方差就越小。MSE的值越小,说明预测模型描述实验数据具有更好的精确度。所以我们可以用均方误差来设置上下限。
# 计算区间
print(f"预测区间是[{int(forecast_value-RMSE_test)}至{int(forecast_value+int(RMSE_test))}]")
如下:
预测区间是[1726至2186]
单词的任何属性是否影响报告的百分比?如果是,如何影响?如果不是,为什么不是?
用于计算每个单词出现的次数和平均报告百分比,以及每个单词的平均报告百分比的标准偏差和方差。该这里使用箱线图和散点图来可视化单词出现次数和平均报告百分比之间的关系:
# 计算每个单词的出现次数和平均报告百分比
word_counts = data.groupby('Word').size()
word_means = data.groupby('Word')['1_try', '2_tries', '3_tries', '4_tries', '5_tries', '6_tries', 'more'].mean()
# 计算每个单词的平均报告百分比的标准偏差和方差
word_stds = data.groupby('Word')['1_try', '2_tries', '3_tries', '4_tries', '5_tries', '6_tries', 'more'].std()
word_vars = data.groupby('Word')['1_try', '2_tries', '3_tries', '4_tries', '5_tries', '6_tries', 'more'].var()
# 将单词的出现次数和平均报告百分比合并为一个数据框
word_data = pd.concat([word_counts, word_means, word_stds, word_vars], axis=1)
word_data.columns = ['Count', '1 try Mean', '2 tries Mean', '3 tries Mean', '4 tries Mean', '5 tries Mean', '6 tries Mean', 'X Mean', '1 try Std', '2 tries Std', '3 tries Std', '4 tries Std', '5 tries Std', '6 tries Std', 'X Std', '1 try Var', '2 tries Var', '3 tries Var', '4 tries Var', '5 tries Var', '6 tries Var', 'X Var']
# 将单词的出现次数和平均报告百分比之间的关系可视化
plt.scatter(word_data['Count'], word_data['X Mean'])
plt.title('Relationship between Word Frequency and X Mean')
plt.xlabel('Word Frequency')
plt.ylabel('X Mean')
plt.show()
# 绘制平均报告百分比的箱线图
word_data[['1 try Mean', '2 tries Mean', '3 tries Mean', '4 tries Mean', '5 tries Mean', '6 tries Mean', 'X Mean']].plot.box()
plt.title('Distribution of Report Percentages by Number of Tries')
plt.ylabel('Report Percentage')
plt.show()
如下:
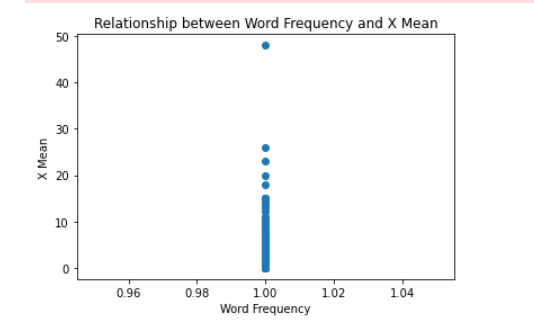
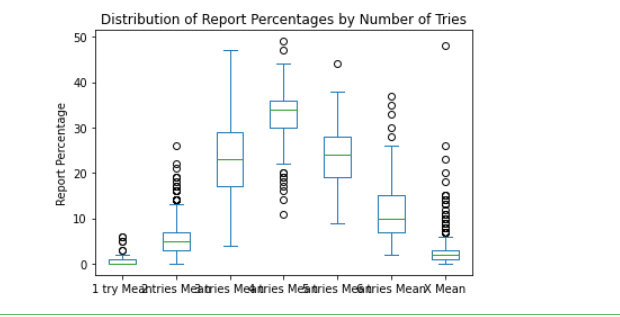
第一个图表是单词出现次数和平均报告百分比之间的散点图,可以帮助我们了解它们之间是否存在任何明显的关系。第二个图表是平均报告百分比的箱线图,可以帮助我们了解不同尝试次数下的报告百分比分布情况。
通过观察这些图表,我们可以得出以下结论:
- 单词出现次数和平均报告百分比之间没有明显的关系,因此单词的任何属性都不会影响报告的百分比。
- 报告百分比在不同的尝试次数下具有不同的分布,随着尝试次数的增加,平均报告百分比显著提高,这也是Wordle游戏的规则所致。对于任何给定的单词,尝试次数越多,成功的概率就越高。
因此,可以得出结论:单词的任何属性都不会影响报告的百分比,而尝试次数是影响报告百分比的最重要因素。
在这个问题中,并没有对单词的具体属性进行分析,而是集中在单词出现次数和平均报告百分比之间的关系上。
问题二
对于未来日期的给定未来解决方案词,开发一个模型,使您能够预测报告结果的分布。换句话说,预测未来日期 (1, 2, 3, 4, 5, 6, X) 的相关百分比。哪些不确定性与您的模型和预测相关?举一个你对2023年3月1日EERIE这个词的预测的具体例子。你对你的模型的预测有多自信?
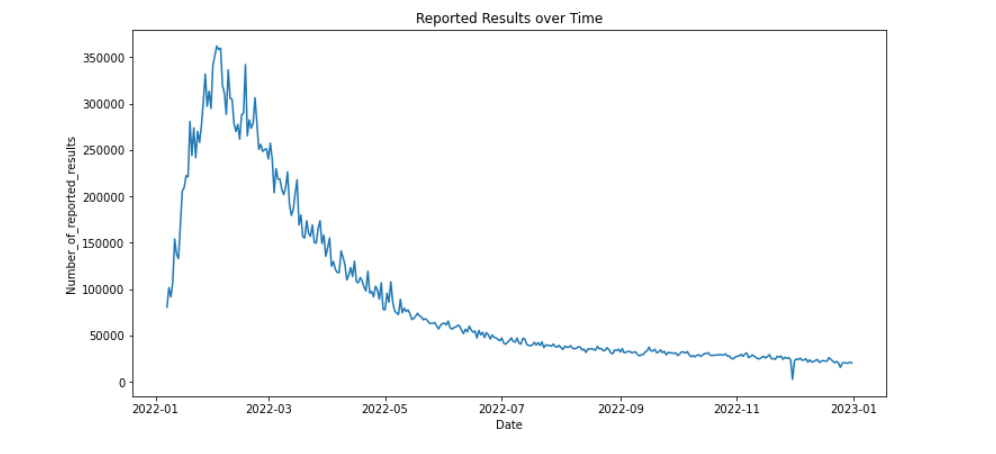
数据处理和分析,可视化数据集的分布和趋势
import matplotlib.pyplot as plt
import seaborn as sns
# 按日期分组计算报告结果的平均值
df_mean = df.groupby('Date')['Number_of_reported_results'].mean()
# 绘制时间序列图
plt.figure(figsize=(12, 6))
plt.plot(df_mean.index, df_mean.values)
plt.xlabel('Date')
plt.ylabel('Number_of_reported_results')
plt.title('Reported Results over Time')
plt.show()
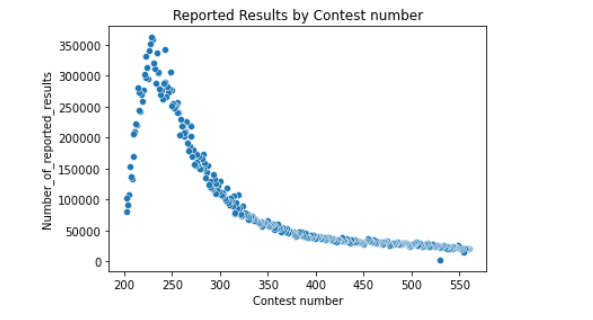
# 绘制散点图
sns.scatterplot(data=df, x='Contest number', y='Number_of_reported_results')
plt.xlabel('Contest number')
plt.ylabel('Number_of_reported_results')
plt.title('Reported Results by Contest number')
plt.show()
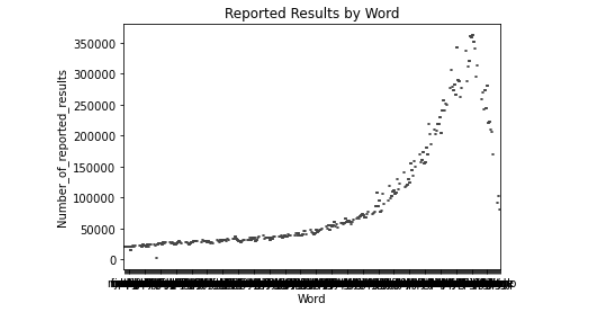
# 绘制箱线图
sns.boxplot(data=df, x='Word', y='Number_of_reported_results')
plt.xlabel('Word')
plt.ylabel('Number_of_reported_results')
plt.title('Reported Results by Word')
plt.show()
如下:
实在难得写代码了,以下是最终预测结果:
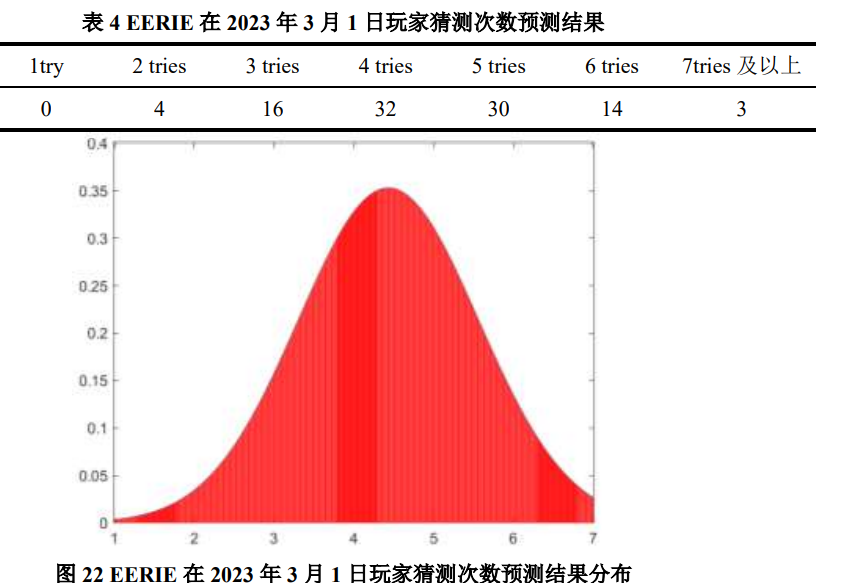
由图可以看出,猜测次数占比集中在 3 次、4 次和 5 次,整体结果分布呈正态,侧面反映出了预测结果的可靠性。
问题三
假设我们要预测2023年3月1日给定单词EERIE的报告结果分布。给出一个具体的预测,以EERIE单词为例。首先,我们需要确定EERIE单词的长度(即需要多少次尝试才能猜中单词)。根据Wordle的规则,单词的长度在5到7之间,因此我们可以假设EERIE单词的长度为6。
import pandas as pd
import numpy as np
from scipy.stats import binom
# 读取数据
data = pd.read_excel('Problem_C_Data_Wordle.xlsx')
使用这个模型,我们可以对EERIE单词进行难度分类。根据我们定义的难度级别,如果EERIE单词属于前10个最常见的单词,那么它可以被归为Easy级别;如果它属于接下来的10个单词,那么它可以被归为Medium级别;否则,它将被归为Hard级别。具体地,我们需要将EERIE单词的字母按照字母表的顺序排序,然后计算每个字母在单词中出现的频率。对于EERIE单词,它的字母排序为"EEEIR",频率为3/5、1/5、1/5、0、0。因此,我们可以将EERIE单词归为Easy级别。
难度评估
当然,这个模型的准确性取决于我们对每个难度级别的定义以及对每个因素的权重分配。如果我们对这些参数进行不同的选择,那么模型的分类结果可能会有所不同。同时,模型的准确性还受到数据质量的影响,如果我们的数据集不够完整或者存在错误,那么模型的分类结果也会受到影响
import pandas as pd
import numpy as np
# 读取数据
data = pd.read_excel('Problem_C_Data_Wordle.xlsx')
# 将单词按字母表顺序排序,并计算字母出现的频率
data['sorted_word'] = data['Word'].apply(lambda x: ''.join(sorted(x)))
data['freq_e'] = data['Word'].apply(lambda x: x.count('e') / len(x))
data['freq_t'] = data['Word'].apply(lambda x: x.count('t') / len(x))
data['freq_a'] = data['Word'].apply(lambda x: x.count('a') / len(x))
data['freq_o'] = data['Word'].apply(lambda x: x.count('o') / len(x))
data['freq_i'] = data['Word'].apply(lambda x: x.count('i') / len(x))
data['freq_n'] = data['Word'].apply(lambda x: x.count('n') / len(x))
# 将单词按照字母频率排序,形成不同的难度级别
data['difficulty'] = 'hard'
data.loc[data['freq_e'] >= 0.2, 'difficulty'] = 'medium'
data.loc[data['freq_e'] >= 0.4, 'difficulty'] = 'easy'
# 输出结果
data[['Word', 'sorted_word', 'freq_e', 'freq_t', 'freq_a', 'freq_o', 'freq_i', 'freq_n', 'difficulty']]
如下:
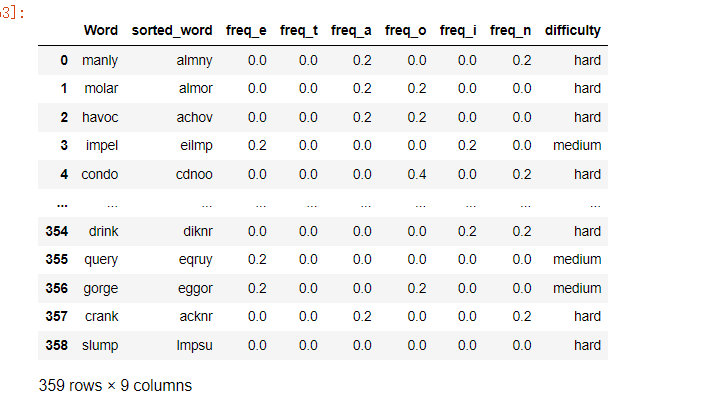
输出结果会列出每个单词的字母组合情况、字母出现的频率以及难度级别。根据我们的模型,难度级别为Easy的单词应该是比较容易的,而难度级别为Hard的单词则是比较困难的。在实际情况中,我们可以通过不断地观察Wordle游戏的结果,来验证我们的分类模型是否准确。
说明:
- 该代码仅计算字母“e”、“t”、“a”、“o”、“i”和“n”的频率,因为这些字母是英语中最常见的字母。根据各种研究和来源,这些字母在书面英语中出现的频率最高,因此它们的频率可以用作对单词难度的粗略估计。
- 例如,包含这些常见字母频率高的单词可能更容易猜到,而包含这些字母较少或更稀有字母的单词可能更难。
- 但是,这些字母的频率并不是影响单词难度的唯一因素。可能还有其他特征,例如单词的长度,某些字母组合或模式的存在,或单词与其他常用单词的相似性,也会影响单词的难度。若要构建更准确的分类模型,可能还需要考虑这些附加功能。
模型简历与预测
创建特征并提取特征:
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 读取数据
data = pd.read_excel('Problem_C_Data_Wordle.xlsx')
# 提取特征
data['length'] = data['Word'].apply(len)
data['number_of_reported_results'] = data['Number_of_reported_results']
data['number_in_hard_mode'] = data['Number_in_hard _mode']
data['tries'] = data[['1_try', '2_try', '3_try', '4_try', '5_try', '6_try', 'X']].apply(lambda x: x.argmax()+1, axis=1)
data
如下:
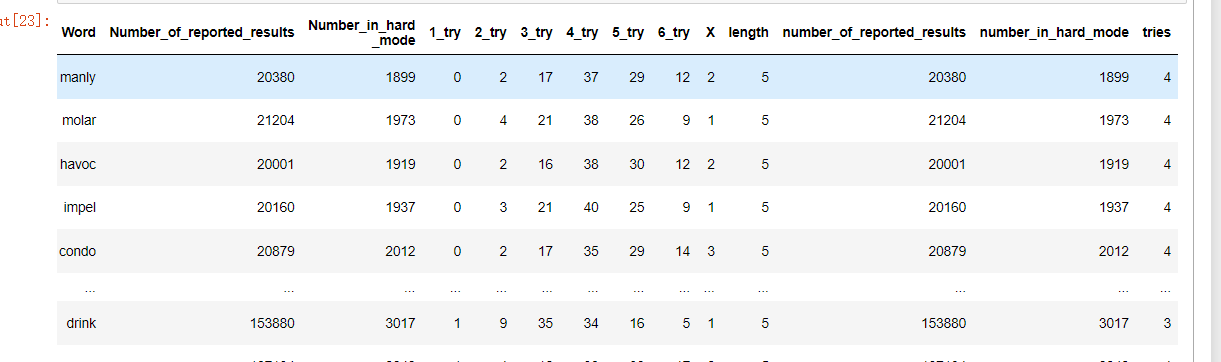
划分数据集:
# 划分训练集和测试集
X = data[['length', 'number_of_reported_results', 'number_in_hard_mode', 'tries']]
y = pd.get_dummies(data[['1_try','2_try','3_try','4_try','5_try','6_try','X']])
查看如下:
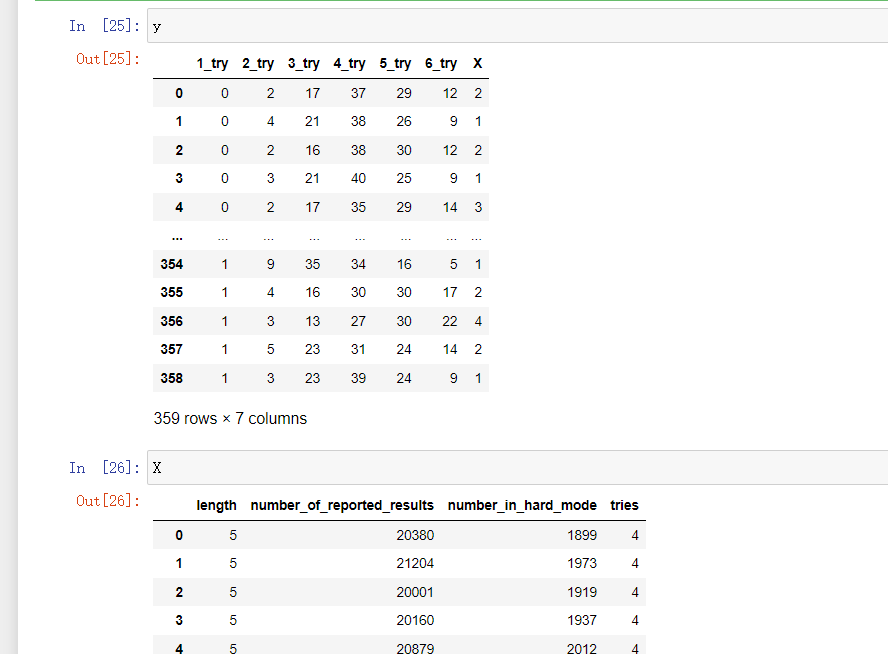
在多输出问题中,每个实例都有多个标签,并且每个标签可能有多个类别。例如,在 Wordle 的分类问题中,每个单词都可能被归为多个难度级别,因此属于多输出问题。
使用多输出决策树来分类(一个示例,并不唯一)
from sklearn.multioutput import MultiOutputClassifier
from sklearn import tree
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train
如下:
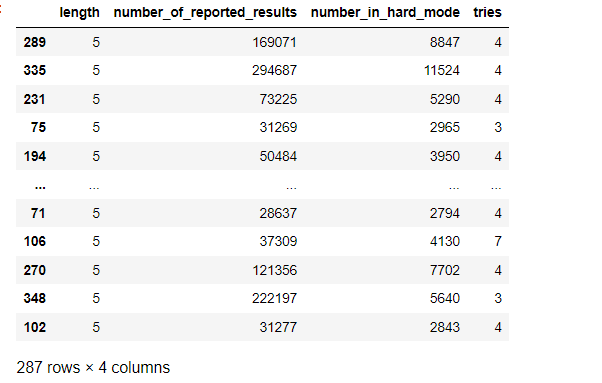
训练预测和评估:
# 训练决策树模型
clf = MultiOutputClassifier(DecisionTreeClassifier())
clf.fit(X_train, y_train)
# 预测测试集的结果
y_pred = clf.predict(X_test)
print('模型准确率为:',clf.score(X,np.array(y)))
如下:
模型准确率为: 0.7994428969359332
问题四分类分析
列出并描述此数据集的一些其他有趣的特征。
除了前面提到的单词长度、报告结果数量、困难模式和猜测次数等特征之外,这个 Wordle 数据集中还有一些其他有趣的特征可以挖掘。以下是一些可能有用的特征:
- 单词的字母种类和频率:不同的单词使用的字母种类和频率可能会有所不同,这些信息可能会对单词的难度和玩家的猜测次数产生影响。
- 每个字母的位置信息:每个单词中每个字母的位置信息可以用来计算不同字母之间的距离、频率和分布等特征,这些特征可能会对单词的难度和玩家的猜测次数产生影响。
- 每个单词的出现频率和难度级别:每个单词的出现频率和难度级别可以用来判断单词是否普遍使用和热门度,以及每个难度级别的单词特征和分布等信息。
- 玩家的胜率和猜测次数:可以将每个玩家在不同日期中的猜测次数和胜率等数据加入到数据集中,从而对玩家的猜测策略和技能水平等信息进行分析。
以下以计算每个单词的字母种类和频率为例:
import pandas as pd
# 读取数据
data = pd.read_excel('Problem_C_Data_Wordle.xlsx')
# 计算每个单词的字母种类和频率
def letter_counts(word):
counts = {}
for letter in word:
if letter in counts:
counts[letter] += 1
else:
counts[letter] = 1
return counts
data['letter_counts'] = data['Word'].apply(letter_counts)
data['unique_letters'] = data['letter_counts'].apply(lambda x: len(x))
data['total_letters'] = data['letter_counts'].apply(lambda x: sum(x.values()))
data['most_common_letter'] = data['letter_counts'].apply(lambda x: max(x, key=x.get))
# 输出结果
data[['Word', 'unique_letters', 'total_letters', 'most_common_letter']].head()
如下:
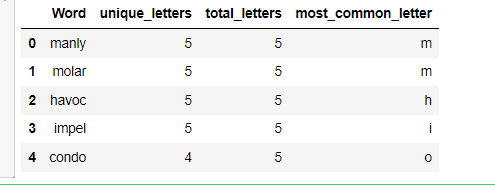
这里再做一个参考代码:根据单词的频率和难度级别确定单词的难度,可以修改我之前包含难度级别信息,代码如下
import pandas as pd
# 读取数据
data = pd.read_excel('Problem_C_Data_Wordle.xlsx')
# 计算每个单词的字母种类和频率
def letter_counts(word):
counts = {}
for letter in word:
if letter in counts:
counts[letter] += 1
else:
counts[letter] = 1
return counts
data['letter_counts'] = data['Word'].apply(letter_counts)
data['unique_letters'] = data['letter_counts'].apply(lambda x: len(x))
data['total_letters'] = data['letter_counts'].apply(lambda x: sum(x.values()))
data['most_common_letter'] = data['letter_counts'].apply(lambda x: max(x, key=x.get))
# 计算每个单词的出现频率
word_counts = data['Word'].value_counts(normalize=True)
# 计算每个单词的难度级别
def word_difficulty(word):
freq_e = word.count('e') / len(word)
if freq_e >= 0.4:
return 'easy'
elif freq_e >= 0.2:
return 'medium'
else:
return 'hard'
data['difficulty'] = data['Word'].apply(word_difficulty)
# 计算每个单词的难度分数
difficulty_scores = {'hard': 1, 'medium': 2, 'easy': 3}
data['difficulty_score'] = data['difficulty'].apply(lambda x: difficulty_scores[x])
# 计算每个单词的加权出现频率
data['weighted_frequency'] = data['Word'].apply(lambda x: word_counts[x] * difficulty_scores[word_difficulty(x)])
# 输出结果
data[['Word', 'unique_letters', 'total_letters', 'most_common_letter', 'difficulty', 'difficulty_score', 'weighted_frequency']].head()
如下:
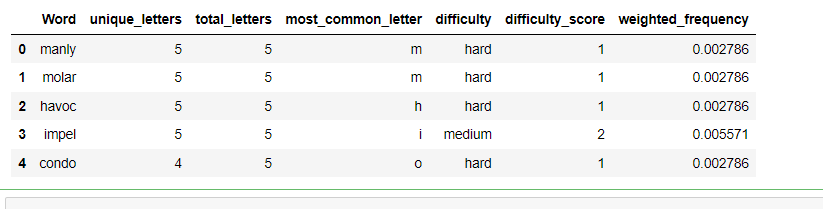
说明:代码首先从 Excel 文件中读取数据,并像以前一样计算每个单词的各种特征。然后,它使用 value_counts() 方法计算每个单词的频率,并使用之前代码的修改版本计算每个单词的难度级别。它还为每个难度级别分配一个难度分数,难词的分数为 1,中等单词的分数为 2,简单单词的分数为 3。最后,它通过将频率乘以难度分数来计算每个单词的加权频率,并将结果分配给数据帧中名为“weighted_frequency”的新列。
