一、简介

ICP算法详解——我见过最清晰的解释_负壹的博客-CSDN博客

两个点集，source和target，target不变，source经过旋转（Rotation）和平移（Translation）甚至加上尺度（Scale）变换，使得变换后的source点集尽量和target点集重合，这个变换的过程就叫点集配准。

  但是ICP的使用方法精度比较差，假如将一个原始点云在X方向上移动一定的距离（或者对原始点云进行降采样），然后进行配准分数也会有很大的差异，并且得到的旋转平移矩阵也差异比较大。

二、基本原理

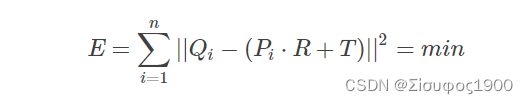
假设用Qi,i=1,2,3,⋯Qi,i=1,2,3,⋯表示第一个点集，Pi,i=1,2,3,⋯Pi,i=1,2,3,⋯表示第二个点集。

ICP配准过程：

1.计算原始点云P中的每个点对于在匹配点云Q的最近点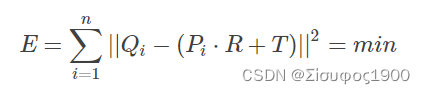

2、 计算对应点的平均最小距离，计算R T 矩阵

3、对原始点云P进行RT转换得到P2

4、计算P2与Q之间的平均最小距离，继续迭代。

提示：这里的目标函数的要求，也可以是迭代次数
 

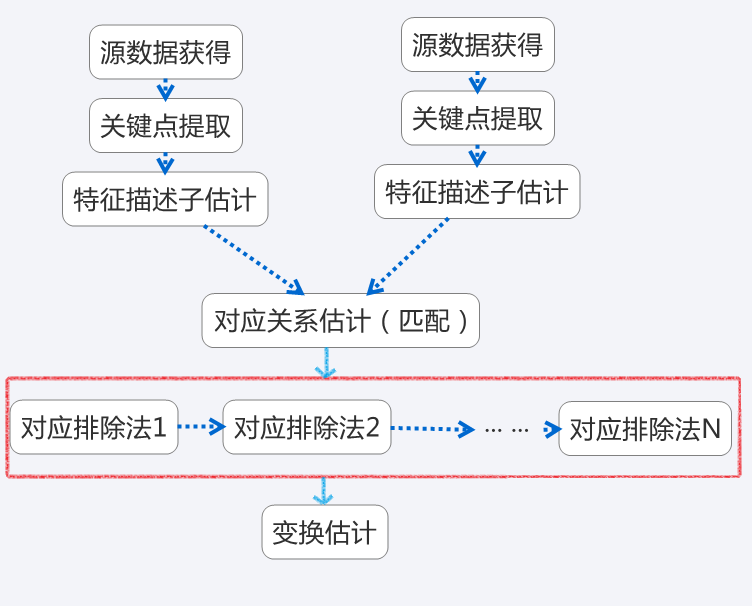
识别步骤：

1、分别找到两个点云数集中的兴趣点或者关键点

2、计算特征描述符

3、分别计算p1(x,y,z） p2(x,y,z)计算特征和位置之间的相关性，通过迭代测试来计算

4、计算之前一定要去除掉点云上面的噪声，ICP是暴力迭代的方法，计算内容是全部点云中的点

5、从特征点总找到一个匹配最好的特征计算出旋转平移矩阵

迭代最近点 Iterative Closest Point （ICP）

PCL学习笔记二：Registration (ICP算法)_rabbif的博客-CSDN博客

 ICP采用最小二乘法的最优配准方法，此算法重复进行点之间的对应关系，计算出一个刚性变换，知道满足收敛的精度。

	// ICP配准
	pcl::IterativeClosestPoint<pcl::PointXYZ,pcl::PointXYZ>icp; // 创建ICP对象  用来ICP配准
	//icp.setMaxCorrespondenceDistance(0.1);  // 
	icp.setTransformationEpsilon(0.1);  // 前一个变换矩阵和当前变换矩阵的差异小于阈值时，就认为已经收敛了，是一条收敛条件
	icp.setEuclideanFitnessEpsilon(0.01);  // 还有一条收敛条件是均方误差和小于阈值， 停止迭代
	icp.setMaximumIterations(10);  // 最大迭代次数
	icp.setInputCloud(cloud_tr);
	icp.setInputTarget(cloud_in);  // 输入目标点云
	icp.align(*cloud_icp);  //配准后的点云

transformation estimation是基于SVD的， SVD是奇异值分解 

基本过程

对于目标点云中的每个点，匹配参考点云（或选定集合）中的最近点。
求得使上述对应点对计算均方根（root mean square，RMS）最小的刚体变换，求得平移参数和旋转参数。
使用获得的转换矩阵来转换目标点云。
迭代（重新关联点），直到满足终止迭代的条件（迭代次数或误差小于阈值）。这里的误差最小，可以是相邻两次均方根差的绝对值小于某一限差。
 

三、代码：

添加头文件

#define BOOST_TYPEOF_EMULATION  //要加在#include <pcl/registration/icp.h>前
#include <pcl/registration/icp.h>   //ICP配准类相关头文件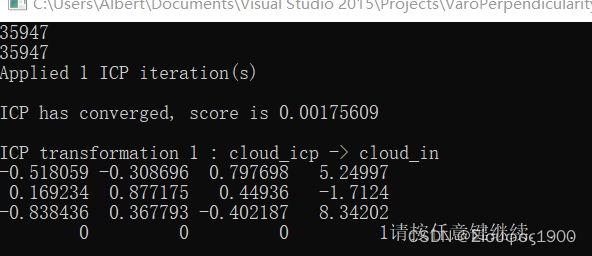

	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_in(new pcl::PointCloud<pcl::PointXYZ>);// 原始点云
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_icp(new pcl::PointCloud<pcl::PointXYZ>);  // ICP 输出点云
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_tr(new pcl::PointCloud<pcl::PointXYZ>);   // 匹配点云
	string strfilepath = "C:\\Users\\Albert\\Desktop\\Binary.pcd";
	if (-1 == pcl::io::loadPCDFile(strfilepath, *cloud_in)) {
		cout << "error input!" << endl;
		return -1;
	}
	cout << cloud_in->points.size() << endl;


	string strfilepath2 = "C:\\Users\\Albert\\Desktop\\Binary2.pcd";
	//if (-1 == pcl::io::loadPCDFile(strfilepath2, *cloud_icp)) {
	//	cout << "error input!" << endl;
	//	return -1;
	//}

	pcl::PointXYZ point;
	for (int i = 0; i < cloud_in->size();i++)
	{
		 point.x= cloud_in->points[i].x + 10;
		 point.y = cloud_in->points[i].y;
		 point.z = cloud_in->points[i].z;
		 cloud_icp->push_back(point);
	}
	cout << cloud_icp->points.size() << endl;

	pcl::io::savePCDFileBinaryCompressed(strfilepath2,*cloud_icp);

	int  iterations = 3;// 默认的ICP的迭代次数
	*cloud_tr = *cloud_icp;

	// ICP配准
	pcl::IterativeClosestPoint<pcl::PointXYZ,pcl::PointXYZ>icp; // 创建ICP对象  用来ICP配准
	//icp.setMaxCorrespondenceDistance(0.1);  // 
	icp.setTransformationEpsilon(0.1);  // 前一个变换矩阵和当前变换矩阵的差异小于阈值时，就认为已经收敛了，是一条收敛条件
	icp.setEuclideanFitnessEpsilon(0.01);  // 还有一条收敛条件是均方误差和小于阈值， 停止迭代
	icp.setMaximumIterations(10);  // 最大迭代次数
	icp.setInputCloud(cloud_tr);
	icp.setInputTarget(cloud_in);  // 输入目标点云
	icp.align(*cloud_icp);  //配准后的点云




	
	if (icp.hasConverged())//icp.hasConverged ()=1（true）输出变换矩阵的适合性评估
	{
		std::cout << "\nICP has converged, score is " << icp.getFitnessScore() << std::endl;
	}
	else
	{
		PCL_ERROR("\nICP has not converged.\n");
		return (-1);
	}

	cout<<icp.getFinalTransformation();