让 new bing 使用 GPT-4 编写一个令人满意的程序全过程赏析

让 new bing 使用 GPT-4 编写一个令人满意的程序全过程赏析
标签:new bing、GPT-4
文章目录
- 让 new bing 使用 GPT-4 编写一个令人满意的程序全过程赏析
- 前言
- 1 让 bing 编写一个画螺旋线的程序
- 1.1 我的要求(1)
- 1.2 bing 的回答全文(1)
- 1.3 bing 编写的程序
- 1.4 程序运行的结果
- 2 让 bing 去掉多余的第一笔
- 2.1 我的要求(2)
- 2.2 bing 的回答全文(2)
- 2.3 我的要求(3)
- 2.4 bing 的回答全文(3)
- 2.5 我的要求(4)
- 2.6 bing 的回答全文(4)
- 2.7 我的要求(5)
- 2.8 bing 的回答全文(5)
- 2.9 bing 编写的程序
- 2.10 程序运行的结果
- 3 改正第二笔起笔没有放下的错误
- 3.1 我的要求(6)
- 3.2 bing 的回答全文(6)
- 3.3 我的要求(7)
- 3.4 bing 的回答全文(7)
- 3.5 bing 编写的程序
- 3.6 程序运行的结果
- 3.7 我的要求(8)
- 3.8 bing 的回答全文(8)
- 3.9 bing 编写的程序
- 3.10 程序运行的结果
- 3.11 我的要求(9)
- 3.12 bing 的回答全文(9)
- 3.13 bing 编写的程序
- 3.14 程序运行的结果
- 3.15 我的要求(10)
- 3.16 bing 的回答全文(10)
- 3.17 我的要求(11)
- 3.18 bing 的回答全文(11)
- 3.19 我的要求(12)
- 3.20 bing 的回答全文(12)
- 4 让画笔箭头方向跟螺旋线方向一致
- 4.1 我的要求(13)
- 4.2 bing 的回答全文(13)
- 4.3 bing 编写的程序
- 4.4 程序运行的结果
- 4.5 我的要求(14)
- 4.6 bing 的回答全文(14)
- 4.7 bing 编写的程序
- 4.8 程序运行的结果
- 结语
前言
前天 Open AI 的 GPT-4上线了,所能达到的高度惊爆人的眼球。上线当天,我就把应用 GPT-4 的新版微软搜索引擎 bing 使用环境配置好了。今天试着用这个 bing 的聊天功能,一步步与 bing 沟通,真还让 bing 替我编写了一个令我满意的 Python 程序。而这个画阿基米德螺旋线的 Python 程序,我在几年前自己 Coding 竟然花了半个月,才达到满意的结果。新科技带来的变化,令人眼花缭乱、一时难以判断走向,是不是很惊恐?
下面就在这里展现、赏析这个聊天过程吧。
1 让 bing 编写一个画螺旋线的程序
1.1 我的要求(1)

1.2 bing 的回答全文(1)
由于 bing Chat 还不支持完整截图,去网页打开吧。点击此处或者复制链接后在 new bing 中打开(需要在 new bing 中登录后才能打开,下同)。
1.3 bing 编写的程序
为了美观,略有改动(step *= 0.99改为step *= 0.999),下同。
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 5 # 螺旋线的起始半径
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度
step = 5 # 螺旋线的步长
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
1.4 程序运行的结果

2 让 bing 去掉多余的第一笔
看上去从原点到螺旋线的起点的那条很短的直线即第一笔不是螺旋线的一部分,是多余的。
2.1 我的要求(2)

2.2 bing 的回答全文(2)
点击此处或者复制链接后在 new bing 中打开。
2.3 我的要求(3)

2.4 bing 的回答全文(3)
点击此处或者复制链接后在 new bing 中打开。
2.5 我的要求(4)

2.6 bing 的回答全文(4)
点击此处或者复制链接后在 new bing 中打开。
2.7 我的要求(5)

2.8 bing 的回答全文(5)
点击此处或者复制链接后在 new bing 中打开。
2.9 bing 编写的程序
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 5 # 螺旋线的起始半径
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度
step = 5 # 螺旋线的步长
# 抬起画笔,不留痕迹(新增代码)
t.penup()
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 放下画笔,开始绘制(新增代码)
t.pendown()
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
2.10 程序运行的结果

3 改正第二笔起笔没有放下的错误
从运行结果看,第一笔前把笔抬起后,没有及时放下,导致后边的笔画全部没有画,需要改正。
3.1 我的要求(6)

3.2 bing 的回答全文(6)
点击此处或者复制链接后在 new bing 中打开。
3.3 我的要求(7)

3.4 bing 的回答全文(7)
点击此处或者复制链接后在 new bing 中打开。
3.5 bing 编写的程序
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 5 # 螺旋线的起始半径
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度
step = 5 # 螺旋线的步长
# 抬起画笔,不留痕迹(新增代码)
t.penup()
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 放下画笔,开始绘制(新增代码)
t.pendown()
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
3.6 程序运行的结果

3.7 我的要求(8)

3.8 bing 的回答全文(8)
点击此处或者复制链接后在 new bing 中打开。
3.9 bing 编写的程序
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 5 # 螺旋线的起始半径
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度
step = 5 # 螺旋线的步长
# 抬起画笔,不留痕迹(新增代码)
t.penup()
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
# 放下画笔,开始绘制(新增代码)
t.pendown()
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
3.10 程序运行的结果

3.11 我的要求(9)

3.12 bing 的回答全文(9)
点击此处或者复制链接后在 new bing 中打开。
3.13 bing 编写的程序
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 5 # 螺旋线的起始半径
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度
step = 5 # 螺旋线的步长
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
if angle > 0: # 如果角度大于0,说明不是第一笔(新增代码)
t.pendown() # 放下画笔,开始绘制(新增代码)
else: # 否则,说明是第一笔(新增代码)
t.penup() # 抬起画笔,不留痕迹(新增代码)
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
3.14 程序运行的结果

至此,必应终于把多余的第一笔去掉了。表扬一下。
3.15 我的要求(10)

3.16 bing 的回答全文(10)
点击此处或者复制链接后在 new bing 中打开。
为了 new bing 以后能正确画出,特意总结了一下,令人发笑的是 new bing 还找了理由推脱。
3.17 我的要求(11)

3.18 bing 的回答全文(11)
(略)
3.19 我的要求(12)

3.20 bing 的回答全文(12)
点击此处或者复制链接后在 new bing 中打开。
4 让画笔箭头方向跟螺旋线方向一致
画笔箭头方向始终朝着右面,感觉怪怪的,让 bing 改一下。
4.1 我的要求(13)

4.2 bing 的回答全文(13)
点击此处或者复制链接后在 new bing 中打开。
4.3 bing 编写的程序
# 导入turtle模块,用于绘图
import turtle
# 导入math模块,用于计算
import math
# 创建一个turtle对象,命名为t
t = turtle.Turtle()
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 10 # 螺旋线的起始半径(修改代码)
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度(修改代码)
step = 5 # 螺旋线的步长
# 移动画笔到原点(0, 0)(新增代码)
t.goto(0, 0)
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
if angle > 0: # 如果角度大于0,说明不是第一笔(新增代码)
t.pendown() # 放下画笔,开始绘制(新增代码)
else: # 否则,说明是第一笔(新增代码)
t.penup() # 抬起画笔,不留痕迹(新增代码)
# 设置画笔朝向与螺旋线方向一致(新增代码)
t.setheading(angle)
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.99
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
4.4 程序运行的结果

还是不正确,画笔箭头方向与螺旋线垂直了。
4.5 我的要求(14)

4.6 bing 的回答全文(14)
(略)
4.7 bing 编写的程序
# 设置画笔的颜色和速度
t.color("blue")
t.speed(0)
# 设置阿基米德螺旋线的参数
a = 10 # 螺旋线的起始半径(修改代码)
b = 0.1 # 螺旋线的增长系数
angle = 0 # 螺旋线的起始角度(修改代码)
step = 5 # 螺旋线的步长
# 移动画笔到原点(0, 0)(新增代码)
t.goto(0, 0)
# 循环绘制阿基米德螺旋线,直到半径超过200像素或角度超过1080度
while a < 200 and angle < 1080:
# 计算阿基米德螺旋线上当前点的极坐标(r, theta)
r = a + b * angle # 半径等于起始半径加上增长系数乘以角度
theta = math.radians(angle) # 角度转换为弧度制
# 计算阿基米德螺旋线上当前点的直角坐标(x, y)
x = r * math.cos(theta) # x坐标等于半径乘以余弦值
y = r * math.sin(theta) # y坐标等于半径乘以正弦值
if angle > 0: # 如果角度大于0,说明不是第一笔(新增代码)
t.pendown() # 放下画笔,开始绘制(新增代码)
else: # 否则,说明是第一笔(新增代码)
t.penup() # 抬起画笔,不留痕迹(新增代码)
# 设置画笔朝向与螺旋线方向一致(新增代码)
t.setheading(angle + 90)
# 移动画笔到当前点,并画出一小段曲线
t.goto(x, y)
# 更新角度和步长,使得曲线更平滑
angle += step
step *= 0.999
# 结束绘图,并保持窗口显示直到用户关闭
turtle.done()
4.8 程序运行的结果
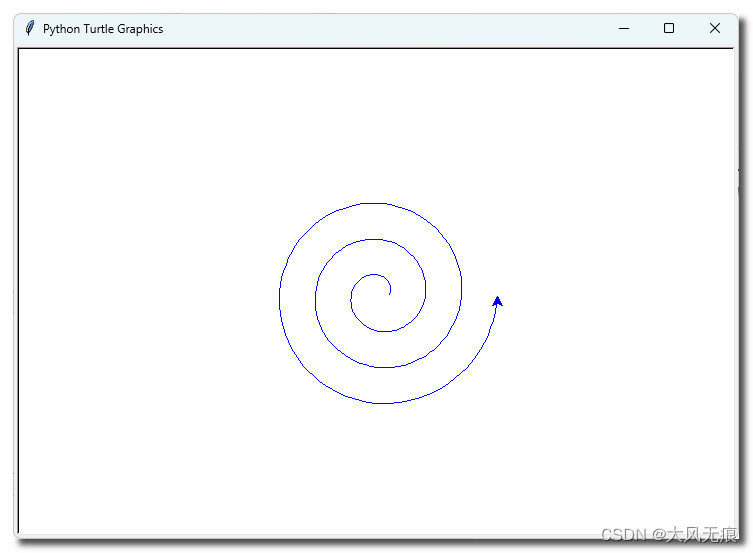
结语
通过与 new bing 沟通,让 bing 为我编写了一个令人满意的程序。从中可以得出以下启发:
- 1、我们需要 new bing 做的事情可以逐步描述,并不需要一次描述清楚;
- 2、new bing 还会犯糊涂,需要不断指正。
