2024春晚刘谦魔术与约瑟夫环问题
各位小伙伴们大家——过~年~好~~~![]~( ̄▽ ̄)~*
昨晚播出2024春节联欢晚会,本着在乡下无聊也是无聊不如看看今年春晚有没有什么乐子的心态从晚上20点到次日0点40共4个多小时人生中首次看完了一整场春晚(((φ(◎ロ◎;)φ)))
刘谦的魔术节目经我和唯一也看了正常春晚直播的小伙伴一致认为是全场最佳!春晚刚结束网上就有大佬给出了第二个魔术(拼扑克牌)的数学模拟,也有大佬发布了代码程序。博主模拟了魔术过程之后也分享一下程序代码。
顺便,借此回顾一下约瑟夫环问题。
目录
一、拼扑克牌魔术编程揭秘
1.过程图解
2.Python代码
二、约瑟夫环问题
1.问题介绍
2.数组实现
思路模拟
代码实现
3.循环链表实现
4.递归实现
一、拼扑克牌魔术编程揭秘
1.过程图解



2.Python代码
用Python语言是因为它对列表操作(切片、拼接等)特别方便:
import random
# 初始卡片cards队列,4张牌,假设为 7,8,9,10
cards = [7, 8, 9, 10]
# 一、把4张牌撕开成8张,放到原来4张牌后
cards += cards
# print(cards)
# 二、名字有几个字,名字有几个字就从队头拿几张牌放到队尾
# 从队头取name_len个元素插入队尾
name_len = int(input('名字长度(2~7的整数):')) # 名字长度
for _ in range(name_len):
cards.append(cards.pop(0))
# print(cards)
# 三、拿起最上面三张,把这三张整体插进剩下卡片的中间任意位置
first_three = cards[:3] # 队首3个元素,待插入
other_cards = cards[3:] # 剩下5个元素
# 队首3个元素插入到剩下5个元素的位置是随机的
index = random.randint(1, 4) # index 可取 1,2,3
cards = other_cards[:index] + first_three + other_cards[index:]
# print(cards)
# 四、把第一张牌放到屁股下
key_card = cards.pop(0)
# 五、按南北方人取牌,重复上述过程
south_north = int(input('南北方人(南方1,北方2,分不清3):')) # 南方人还是北方人
first_cards = cards[:south_north]
other_cards = cards[south_north:]
# 插入的位置是随机的
index = random.randint(1, 7 - south_north - 1)
cards = other_cards[:index] + first_cards + other_cards[index:]
# print(cards)
# 六、按性别取牌,并撒出去
gender = int(input('性别(男1,女2):')) # 性别
for _ in range(gender):
cards.pop(0)
# print(cards)
# 七、洗牌,“见证奇迹的时刻”
for _ in range(7):
cards.append(cards.pop(0))
# print(cards)
# 此时若为女,队尾元素调整至倒数第3;若为男,倒数第2
# 八、好运留下来,烦恼丢出去
while len(cards) > 1:
# 好运留下来
cards.append(cards.pop(0))
# 烦恼丢出去
cards.pop(0)
# print(cards)
print(f"assert cards[0] == key_card ? :{cards[0] == key_card}")
运行结果:


二、约瑟夫环问题
1.问题介绍
“约瑟夫环问题”也叫“丢手绢问题”。百度百科介绍了此问题的起源:
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。
问题是,给定了和,一开始要站在什么地方才能避免被处决?Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
可以把分析约瑟夫环问题的过程总结成以下步骤:
- 总共有 N 个人围成一桌坐下,编号从 1 到 N,从编号为 1 的人开始报数。
- 报数也从 1 开始,报到 M 的人出局,从出局者的下一位在座成员开始继续从 1 开始报数。
- 重复这个过程求各成员的出局次序,或求最后一个在座的成员编号。
为了便于接下来的讨论,这里取约瑟夫环问题的一个具体的变式:
30个人在一条船上,船只超载,现需15人下船。于是人们排成一队,排队的位置即为他们的编号。人们循环报数,从1开始,数到9的人下船。如此循环,直到船上仅剩15人为止,问:都有哪些编号的人下船了?
2.数组实现
思路模拟
数组实现的方式非常简单,我们可以直接进行以下模拟:
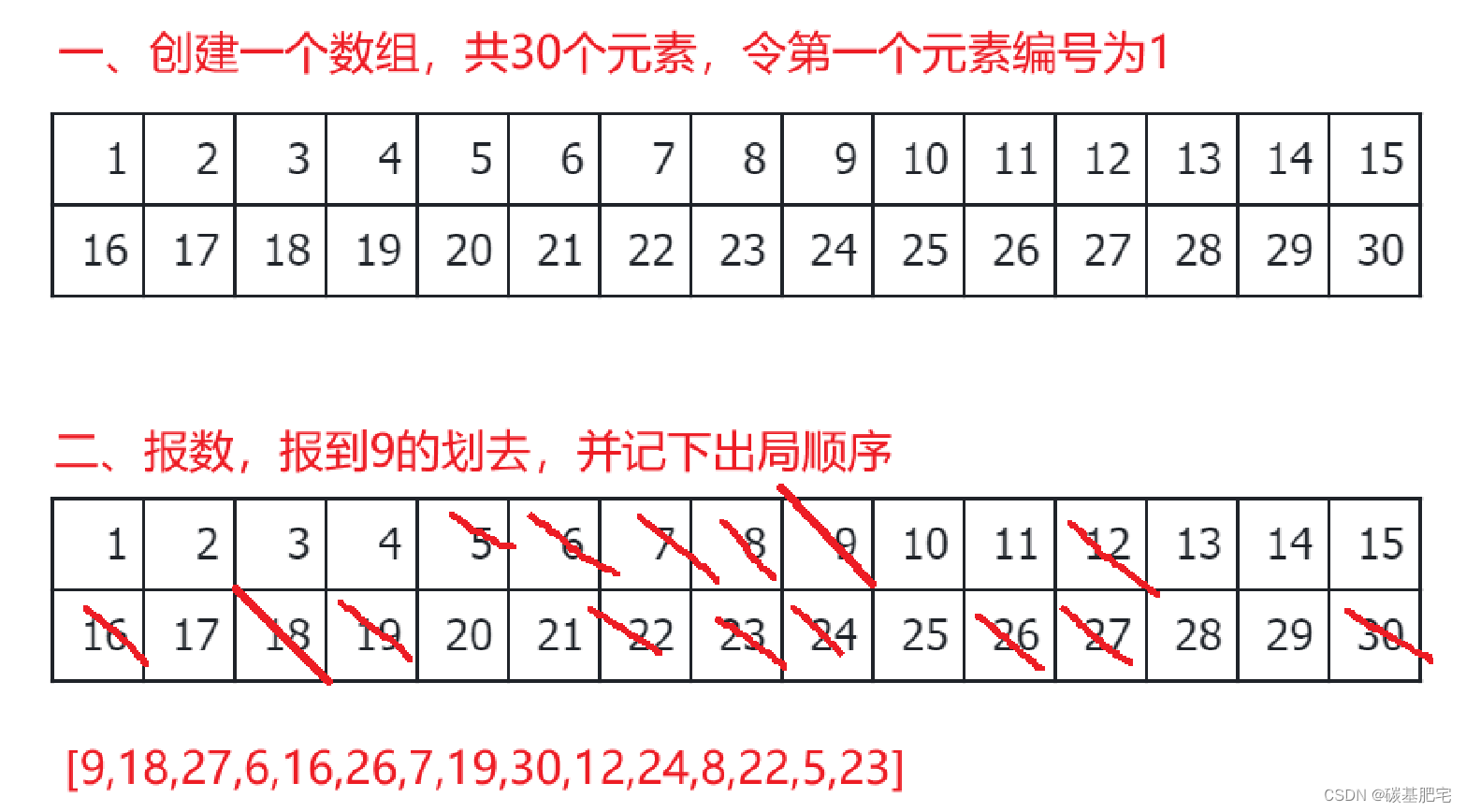
代码实现
import java.util.Scanner;
public class Solution1 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("共有 n 人:");
int n = scanner.nextInt(); // n 为总人数
System.out.print("数到数字 m 时出局:");
int m = scanner.nextInt(); // 数到 m 时出局
System.out.print("要留下多少人:");
int peopleLeft = scanner.nextInt(); // 要留下的人数
int[] flag = new int[n + 1]; // 用于标记某位置的人是否还在船上,0表示未出局,1表示已出局
int cnt = 0, i = 0, k = 0; // cnt:目前已出局的人数,i:某位置的人,k:当前报的数
while (cnt != peopleLeft) {
// 从第一个人依次进行报数
i += 1;
if (i > n) {
i = 1;
}
if (flag[i] == 0) { // 如果 i 位置的人未出局
k += 1; // 就报一个数
if (k == m) { // 如果报到要求出局的数 m
flag[i] = 1; // 标记为出局
cnt += 1; // 已出局人数+1
System.out.print(i + " "); // 打印出局的人的位置
k = 0; // 清空k,下次重新从0开始报数
}
}
}
}
}
运行结果:
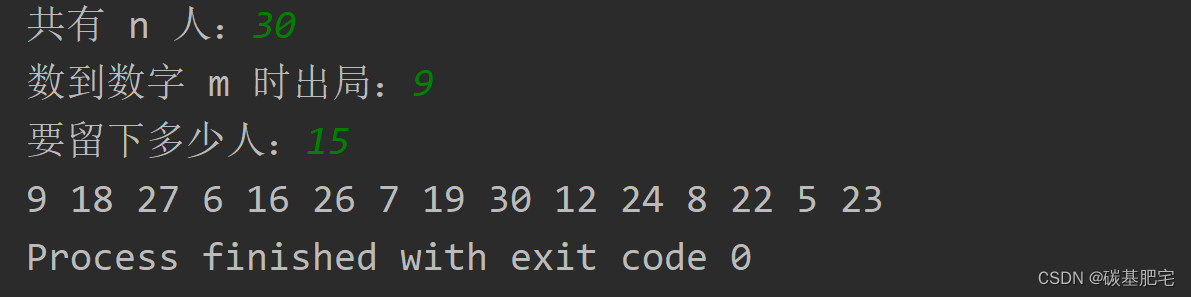
3.循环链表实现
4.递归实现
(先去拜个年,拜完年回来补~)
