机器学习聚类算法
聚类算法是一种无监督学习方法,用于将数据集中的样本划分为多个簇,使得同一簇内的样本相似度较高,而不同簇之间的样本相似度较低。在数据分析中,聚类算法可以帮助我们发现数据的内在结构和规律,从而为进一步的数据分析和挖掘提供有价值的信息。
聚类算法在现实中的应用:用户画像,广告推荐,搜索引擎的流量推荐,恶意流量识别,新闻聚类,筛选排序;图像分割,降维,识别;离群点检测;
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算方法,会得到不同的聚类结果。
K-Means算法
K-means是一种基于划分的聚类算法,其基本原理是通过迭代计算,将数据集划分为K个簇,使得每个簇内的数据点到该簇中心的距离之和最小。
K-means算法的主要步骤:
- 初始化:选择K个初始质心;
- 分配:将每个数据点分配到距离最近的质心所在的簇;
- 更新:重新计算每个簇的质心;
- 迭代:重复分配和更新步骤,直到质心不再发生变化或达到最大迭代次数。
K-means算法适用于球形簇分布的数据,对噪声和异常值较为敏感,需要预先指定簇的数量K。
层次聚类算法
层次聚类是一种基于树形结构的聚类方法,通过计算数据点之间的距离,逐步将数据点合并为更大的簇。层次聚类可以分为凝聚型(自下而上)和分裂型(自上而下)两种方法。
- 初始化:将每个数据点视为一个簇;
- 合并:计算簇之间的距离,将距离最近的两个簇合并为一个新的簇;
- 迭代:重复合并步骤,直到所有数据点合并为一个簇或达到预设的簇数量。
层次聚类不需要预先指定簇的数量,可以发现任意形状的簇,但计算复杂度较高,不适合处理大规模数据集。
DBSCAN算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,其基本原理是通过定义数据点的邻域半径和邻域密度阈值,将相互靠近且密度相近的数据点划分为一个簇。
- 初始化:选择一个尚未访问的数据点;
- 扩展:如果该数据点的邻域内有足够多的数据点,则将其纳入当前簇,并继续扩展邻域;
- 迭代:重复扩展步骤,直到所有数据点被访问。
DBSCAN算法可以发现任意形状的簇,对噪声和异常值具有较好的鲁棒性,需要预先设定邻域半径和密度阈值。
KMeans Api
sklearn.cluster.KMeans(n_clusters=8)
-
参数:n_clusters:开始的聚类中心数量
estimator.fit(x)
estimator.predict(x)
estimator.fit_predict(x)案例
随机创建不同二维数据集作为训练集,并结合k-means算法将其聚类 。
聚类参数n_cluster传值不同,得到的聚类结果不同。
make_blobs函数是用于生成模拟数据的函数,它返回一个包含样本数据和对应标签的元组
n_samples:表示要生成的样本数量,默认为100。n_features:表示每个样本的特征数量,默认为2。centers:表示类别的中心点坐标,可以是一个列表或数组,其中每个元素代表一个类别的中心点坐标。在给定的示例中,有4个类别,分别位于(-1, -1)、(0, 0)、(1, 1)和(2, 2)。cluster_std:表示每个类别的标准差,可以是一个列表或数组,其中每个元素代表一个类别的标准差。在给定的示例中,有4个类别,它们的标准差分别为0.4、0.2、0.2和0.2。random_state:表示随机数生成器的种子,用于控制随机性。在给定的示例中,随机数生成器的种子设置为9。
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
# 数据集可视化
plt.scatter(X[:, 0], X[:, 1]')
plt.show() 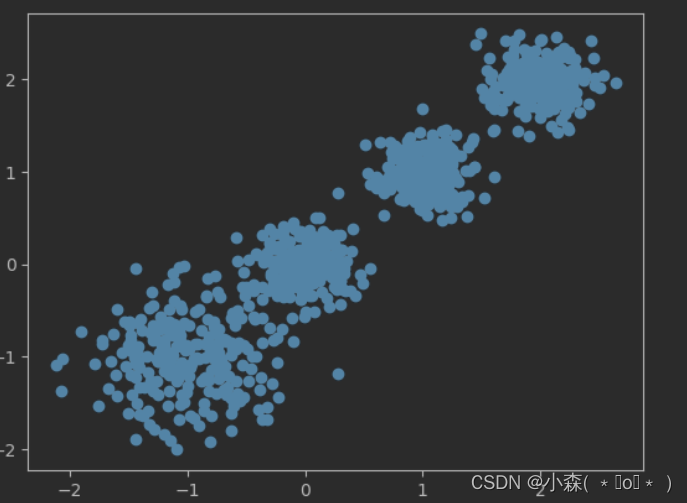
使用k-means进行聚类,并使用silhouette_score评估
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
print(silhouette_score(X, y_pred))
# 0.6634549555891298 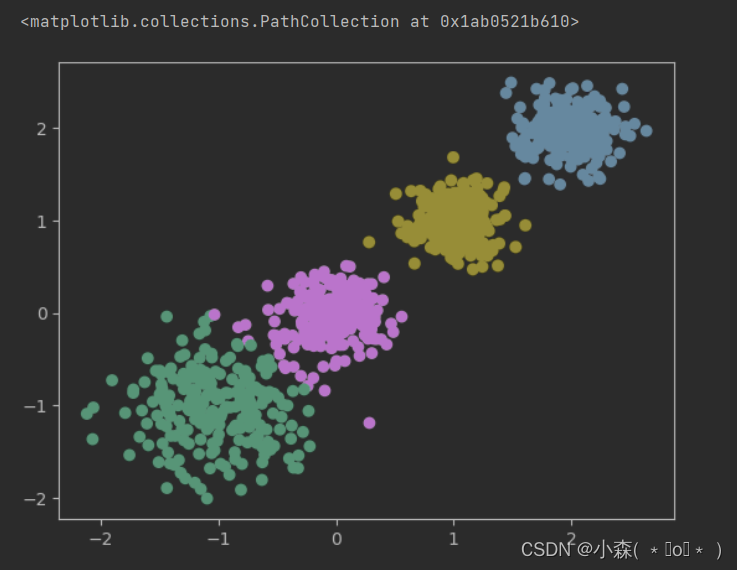
K-Means聚类步骤
- K表示初始中心点个数(计划聚类数)
-
means求中心点到其他数据点距离的平均值
-
随机设置K个特征空间内的点作为初始的聚类中心
-
对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
-
接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点。
-
如果计算得出的新中心点与原中心点一样那么结束,否则重新进行第二步过程。
模型评估
聚类算法模型评估通常涉及多种指标,这些指标可以帮助我们了解聚类的效果和质量。
- SSE(Sum of Squared Errors):SSE计算的是聚类中心与各个样本点之间误差的平方和。它衡量的是簇内紧密程度,即簇内样本与聚类中心的相似度。SSE越小,表示簇内样本越紧密,聚类效果越好。
- 轮廓系数(Silhouette Coefficient):轮廓系数结合了簇内的凝聚力和簇间的分离力,是一种基于样本之间距离的评估指标。它的值域在-1到1之间,值越大表示聚类效果越好。
- Calinski-Harabaz指数(CH指数):CH指数基于簇内和簇间的协方差计算,值越大表示聚类效果越好。它适用于簇大小差不多的情况。
- Davies-Bouldin指数(DB指数):DB指数是基于样本之间距离的评估指标,它评估的是簇之间的分离度。DB指数越小,表示簇之间的分离度越好,聚类效果越佳。
Elbow method — K值确定
方法的基本思想是:
- 对于不同的K值,计算每个K值对应的总内平方和(Within-Cluster-Sum of Squared Errors),即每个样本点到其所属簇质心的距离的平方和。
- 随着K值的增加,WCSS会逐渐减小,因为更多的簇意味着样本点与其质心的平均距离更小。
- 绘制WCSS随K值变化的折线图,通常会出现一个“肘点”(elbow point),即WCSS下降速度明显变慢的地方。
- “肘点”对应的K值被认为是较优的簇数量,因为它在减少误差的同时,并没有大幅增加簇的数量。
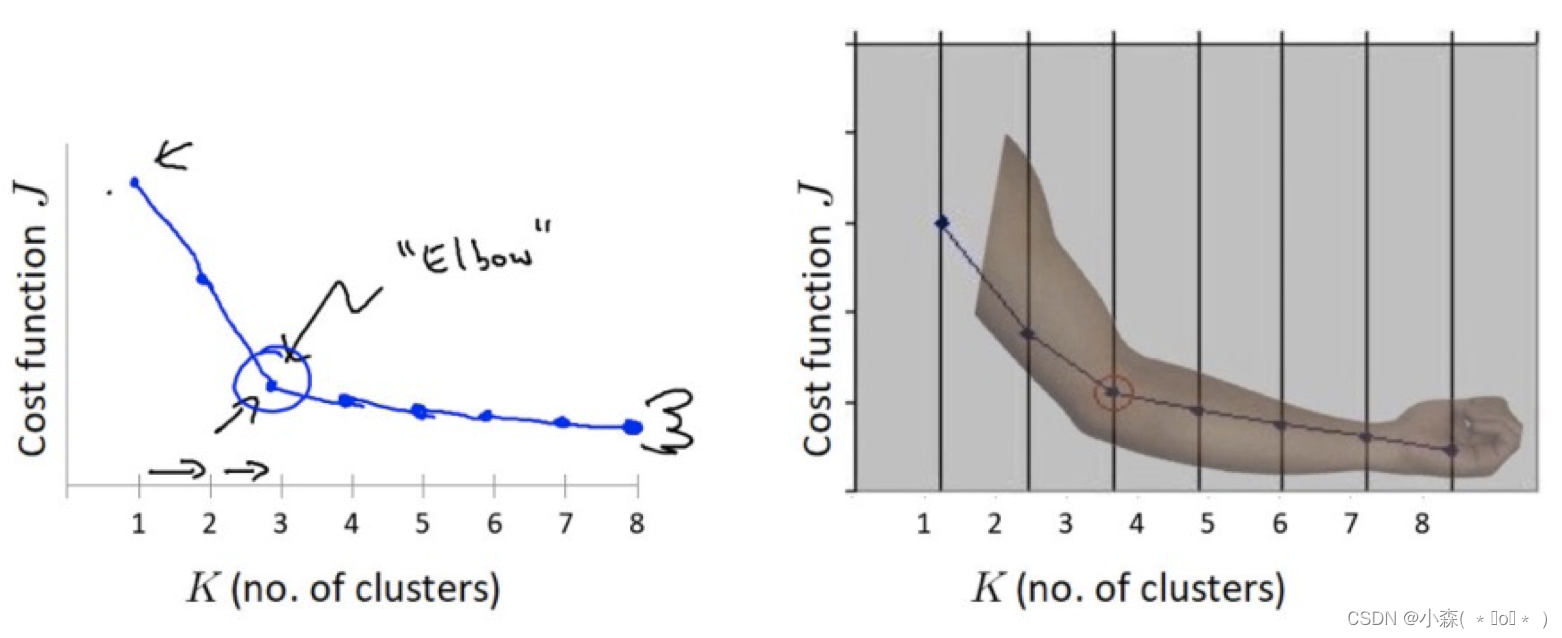
下降率突然变缓时即认为是最佳的k值。
轮廓系数法
结合聚类的凝聚度和分离度,用于评估聚类的效果,使其内部距离最小化,外部距离最大化
计算样本到同簇其他样本的平均距离 ,距离越小样本的簇内不相似度越小,说明样本越应该被聚类到该簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1],系数越大,聚类效果越好。
每次聚类后,每个样本都会得到一个轮廓系数,为1时,说明这个点与周围簇距离较远,结果非常好,为0,说明这个点可能处在两个簇的边界上,当值为负时,该点可能被误分了。
