数据结构——5.4 树、森林
5.4 树、森林
- 概念

-
树的存储结构
-
双亲表示法
-
孩子表示法
-
孩子兄弟表示法(二叉树表示法):
二叉树每个结点有三个变量
① 二叉树结点值:原树结点的值
② 二叉树左孩子:原树结点的最左孩子
③ 二叉树右孩子:原树结点的紧邻右兄弟
该二叉树有一个特点:根节点只有左子树
-
-
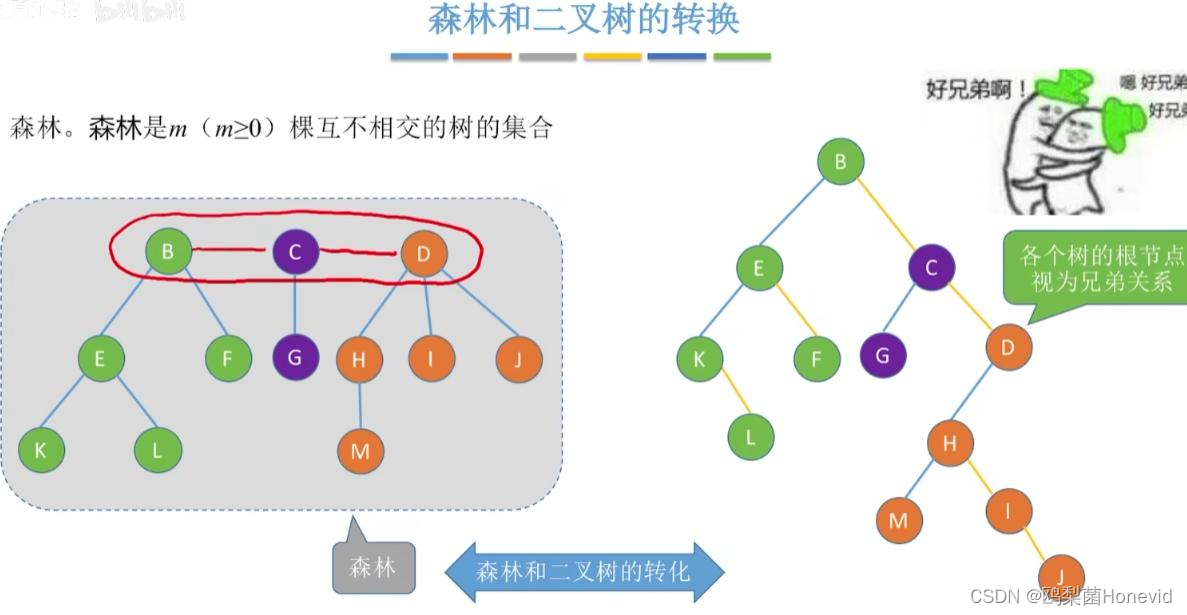
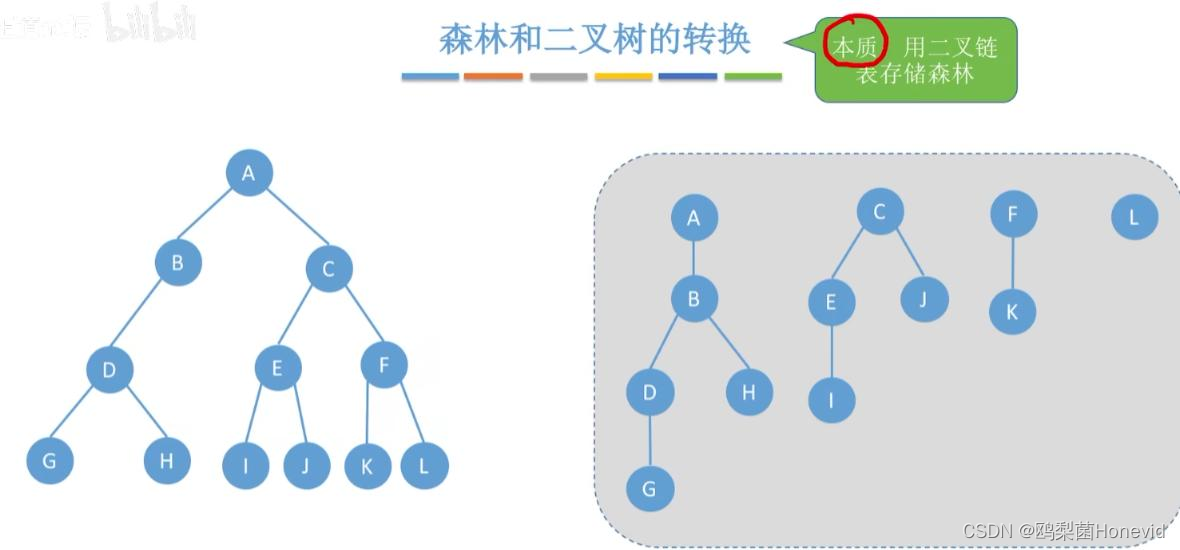
森林和二叉树的转换
-
把森林中每一棵树都转换成二叉树(根节点只有左子树)
-
相邻树的根节点作为左右兄弟,从而可以填补作为各二叉树的右子树
-
-
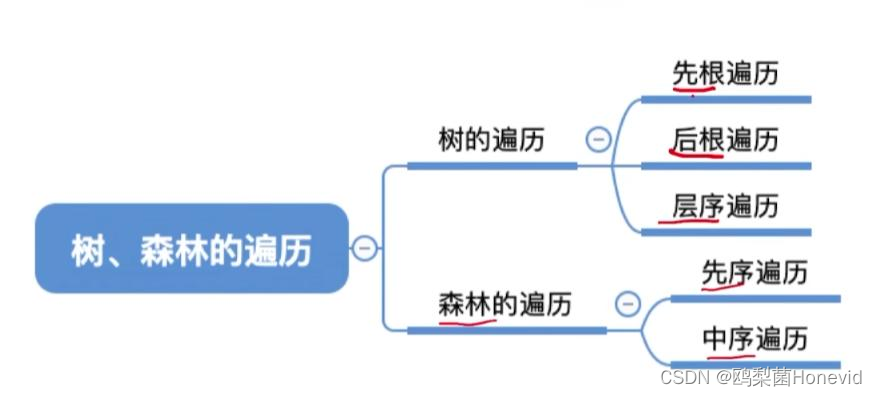
树和森林的遍历
-
树的遍历
-
先根遍历:先访问根节点,再依次从左至右先根遍历子树(即第一次路过就标记)
(与该树对应二叉树的先序序列相同)(深度优先遍历)
-
后根遍历:先对各个子树对后根遍历,再访问根节点(即第三次路过才标记)
(与该树对应二叉树的中序序列相同)(深度优先遍历)
-
层次遍历:(用队列辅助实现)每次结点出队,就将其孩子结点从左至右入队(广度优先遍历)
-
-
森林的遍历
-
先序遍历:从左至右先根遍历各个树(与该森林对应二叉树的先序序列相同)
-
中序遍历:从左至右后根遍历各个树(与该森林对应二叉树的中序序列相同)
-
-

- 理解
-
二叉链表存储森林时,根节点的右节点为森林左起第二棵的根,森林可能只有一棵树,因此根节点的右节点可能为空
-
森林转换成二叉树后,二叉树的左子为森林结点的左孩子,右子为森林结点的右兄弟,左左子,右右兄。
-
如果两个结点是兄弟关系,那么必定有一条右直线连接两个结点,否则不是
-
树的重要性质:n个结点的树,有n-1条边
-
森林的重要性质:n棵树的森林,有m个结点,则有m-n个边。
- 技巧
-
二叉链表存储森林时,根节点的右节点为森林左起第二棵的根,森林可能只有一棵树,因此根节点的右节点可能为空
-
森林原有n个非终端结点,二叉树没有右子树的结点,即为没有右兄弟的结点,共有:(n+1个)(右指针域为空)
-
每个非终端结点的最右孩子没有右兄弟(n个)
-
森林最右树的根节点没有右子树(1个)
-
-
森林或树的叶结点数=二叉树左子树为空结点数
