机器学习算法——决策树详解
文章目录
- 前言:
- 决策树的定义
- 熵和信息熵的相关概念
- 信息熵的简单理解
- 经典的决策树算法
- ID3算法
- 划分选择或划分标准——信息增益
- ID3算法的优缺点
- C4.5算法
- 信息增益率
- 划分选择或划分标准——Gini系数(CART算法)
- Gini系数计算举例
- CART算法的优缺点
- 其他比较
- 连续值的处理
- ID3和C4.5的结果比较
- C4.5的剪枝
- Python实现案例
- 决策树的可视化
前言:
你是否玩过二十个问题的游戏,游戏的规则很简单:参与游戏的一方在脑海里想某个事物,其他参与者向他提问题,只允许提20个问题,问题的答案也只能用对或错回答。问问题的人通过推断分解,逐步缩小待猜测事物的范围。决策树的工作原理与20个问题类似,用户输人一系列数据,然后给出游戏的答案。
我们经常使用决策树处理分类问题,近来的调查表明决策树也是最经常使用的数据挖掘算法。它之所以如此流行,一个很重要的原因就是使用者基本上不用了解机器学习算法,也不用深究它是如何工作的。
在进行决策树的正式讲解之前,我们先来思考一个生活中常见的小问题。
问题:周末是否看电影?
思考过程:
(1)今天是否是周末?如果不是就不去看电影,如果是就继续思考下一个问题。
(2)工作是否完成?如果还没有完成就不去看电影,如果已经完成就继续思考下一个问题。
(3)今天是晴天吗?如果不是晴天就不去看电影,如果是晴天就继续思考下一个问题。
(4)今天能不能在电影院找到好位置?如果不能就不去看电影,如果能就去看电影。

决策树的定义
- 决策树(Decision Tree)是从一组无次序、无规则,但有类别标号的样本集中推导出的、树形表示的分类规则。
- 一般的,一棵决策树包含一个根结点、若干个内部结点(中间结点)和若干个叶子结点。
- 树的叶子结点表示类别标号,即分类属性的取值,也可以说是决策结果;树的内部结点为条件属性,每个结点包含的样本集合根据属性测试结果被划分到子结点中;根结点包含样本全集。从树根到叶子结点的一条路径称为一条决策规则,它可以对未知数据进行分类或预测。每条有向边都用其出点的属性值标记,如“晴天”“多云”“雨天”是其出点“天气”属性的三种取值。
- 通常,一个属性有多少种取值,就从该结点引出多少条有向边,每一条边代表属性的一种取值。
- 树深度是树根到树叶的最大层数,通常作为决策树模型复杂度的一种度量。
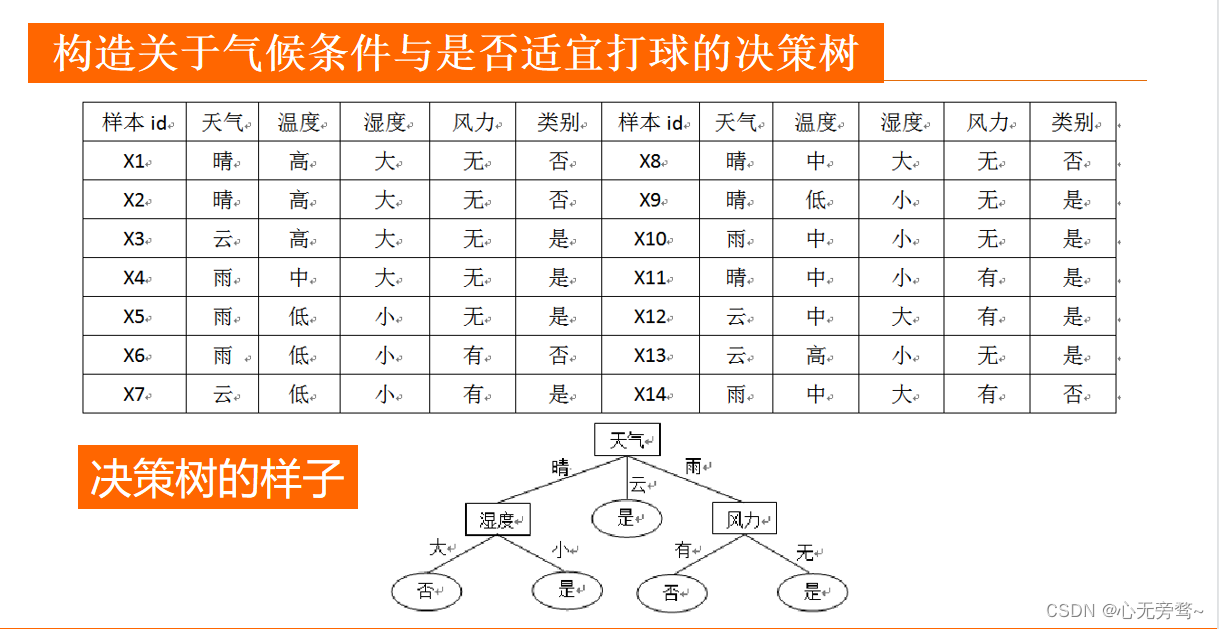
几个小问题
思考:谁来作为根结点?为什么根结点是天气而不是湿度或者风力?
问题1:如何选择条件属性(内部结点)进行划分?
问题2:什么情况下可以选择结束划分?
一般而言,划分数据集的最大原则是:将无序的数据变得更加有序。
将原始数据集通过条件属性被划分为两个或两个以上的子集后,划分的各个子集更“纯”,即划分后的任意一个数据集里面的样本都尽可能地属于同一个类别。
那么,如何衡量集合的“纯”度呢?决策树算法采用了在划分数据集之前或之后使用信息论度量信息的内容。如何使用信息论来度量集合的纯度呢?决策树算法使用了信息熵这个度量指标来衡量集合的纯度。
熵和信息熵的相关概念
- 熵(Entropy)这个概念最早出现在热力学中。它的物理意思表示该体系的混乱程度。简单地说,如果该体系下的分子运动杂乱程度增加,则该体系的熵也随之增加。
- 在熵这个概念普及之后,1948年,信息论之父克劳德·艾尔伍德·香农提出了信息熵的概念,用来描述信息的混乱程度或者信息的不确定度。(据说香农的墓碑上只刻了信息熵的计算公式。)
信息熵的简单理解
假设变量X的随机取值为
X
=
{
x
1
,
x
2
,
.
.
.
,
x
n
}
X=\{x1,x2,...,xn\}
X={x1,x2,...,xn},每一种取值的概率分别是
{
p
1
,
p
2
,
p
3
,
.
.
.
p
n
}
\{p1,p2,p3,...pn \}
{p1,p2,p3,...pn},则变量X 的熵为:
H
(
X
)
=
−
∑
i
=
1
n
p
i
l
o
g
2
p
i
H(X)=-\displaystyle \sum^{n}_{i=1}p_ilog^{p_i}_{2}
H(X)=−i=1∑npilog2pi
- 如果有4个球,1个颜色。
则该颜色的球所占比例为1,可计算该集合的信息熵 = − 1 ∗ l o g 2 ( 1 ) = 0 =-1*log_2(1)=0 =−1∗log2(1)=0 - 如果有4个球,4个不同颜色。
则每种颜色的球所占比例为1/4,可计算该集合的信息熵 = − 4 ∗ 1 / 4 ∗ l o g 2 ( 1 / 4 ) = 2 =-4*1/4*log_2(1/4)=2 =−4∗1/4∗log2(1/4)=2 - 如果有8个球,8个不同颜色。
则每种颜色的球所占比例为1/8,可计算该集合的信息熵 = − 8 ∗ 1 / 8 ∗ l o g 2 ( 1 / 8 ) = 3 =-8*1/8*log_2(1/8)=3 =−8∗1/8∗log2(1/8)=3
可见,系统的熵最小为0,最大可以无穷。熵越小,说明集合的纯度越高。
经典的决策树算法
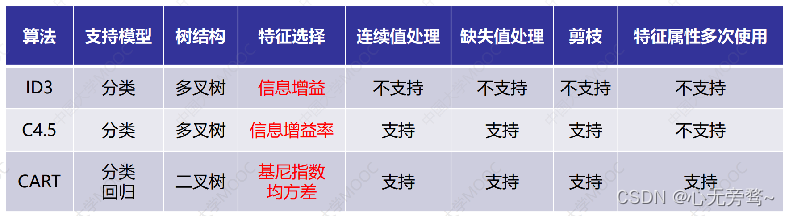
- Hunt算法:最早的决策树算法是由Hunt等人于1966年提出,Hunt算法是许多决策树算法的基础,包括ID3、C4.5和CART等。
- ID3:1979年由澳大利亚的计算机科学家罗斯·昆兰所发表。其他科学家也根据ID3算法相继提出了ID4和ID5等算法。
- C4.5:考虑到ID4等名已被占用,昆兰只好将1993年更新的ID3算法命名为C4.5算法。
- CART:Classification and Regression Tree,可解决分类和回归问题。
ID3算法
划分选择或划分标准——信息增益
- 集合S的信息熵计算(划分前的信息熵)
设有限个样本点集合S,分类属性为
C
=
{
C
1
,
C
2
,
…
,
C
k
}
C=\{C_1, C_2,…, C_k\}
C={C1,C2,…,Ck},假设当前样本集合S中第i类(即Ci)样本所占的比例(或称其为概率)为
p
i
(
i
=
1
,
2
,
.
.
.
,
k
)
pi(i=1,2,...,k)
pi(i=1,2,...,k),则样本集S的信息熵为:
E
(
S
)
=
−
∑
i
=
1
k
p
i
l
o
g
2
p
i
E(S)=-\displaystyle\sum^{k}_{i=1}p_ilog^{p_i}_2
E(S)=−i=1∑kpilog2pi
-
各个自己的信息熵之和(划分后的信息熵)
假设条件属性A有V个可能的取值 { a 1 , a 2 , … , a v } \{a_1, a_2, …, a_v\} {a1,a2,…,av},若使用A来对样本集S进行划分,则会产生V个分支结点,即得到S的V个子集 { S 1 , S 2 , … , S v } \{S_1, S_2, …, S_v\} {S1,S2,…,Sv},其中, S i ( i = 1 , 2 , . . . , v ) S_i(i=1,2,...,v) Si(i=1,2,...,v)中包含了S中所有在属性a上取值为ai的样本。可根据上面给出的式子计算出 Si的信息熵,再考虑到不同分支结点所包含的样本数不同,给分支结点赋予权重 ∣ S i ∣ ∣ S ∣ \frac{| S_i|}{|S|} ∣S∣∣Si∣,即样本数越多的分支结点的影响越大,从而可得用属性A对样本集S进行划分后的信息熵。我把这个熵理解为所有子集的信息熵之和。 -
信息增益(划分前-划分后)
为了测试条件属性A的效果,需要比较父结点与子结点之间的纯度差异,这种差异越大,则说明该测试条件越好,即该条件属性的分类能力越强,而信息增益(information gain)则是这种差异的判断标准。用条件属性A划分样本集合S所得的信息增益为:
G a i n ( S , A ) = E ( S ) − E ( S , A ) Gain(S,A)=E(S)-E(S,A) Gain(S,A)=E(S)−E(S,A)
一般而言,信息增益越大,则意味着使用属性A来进行划分所获得的“纯度提升”更大。因此,可采用信息增益来进行决策树的划分属性选择。
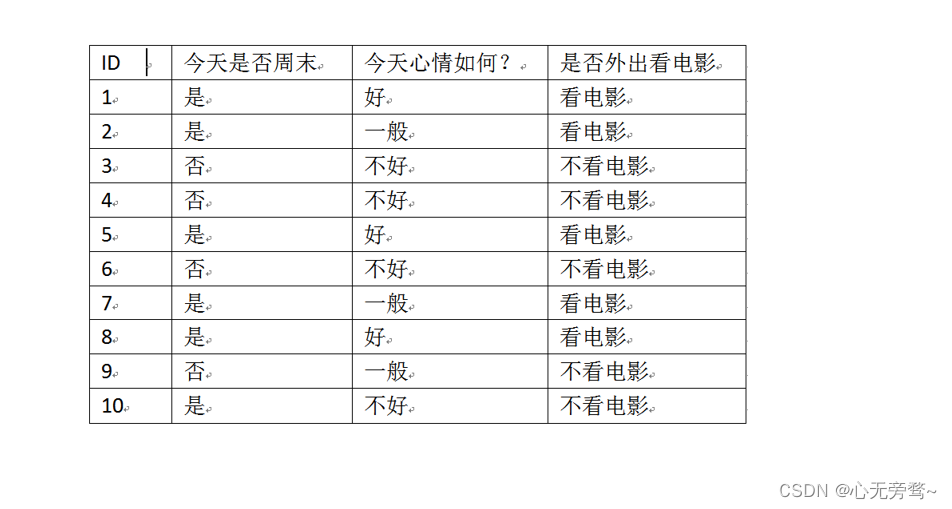
经过计算可得:
G
a
i
n
(
S
,
A
=
”今天是否周末”
)
=
E
(
S
)
−
E
(
S
,
A
=
”今天是否周末”
)
=
1
−
0.39
=
0.61
Gain(S,A=”今天是否周末”)=E(S)-E(S,A=”今天是否周末”)=1-0.39=0.61
Gain(S,A=”今天是否周末”)=E(S)−E(S,A=”今天是否周末”)=1−0.39=0.61
G
a
i
n
(
S
,
A
=
”今天心情如何?”
)
=
E
(
S
)
−
E
(
S
,
A
=
”今天心情如何?”
)
=
1
−
0.2754
=
0.7246
Gain(S,A=”今天心情如何?”)=E(S)-E(S,A=”今天心情如何?”)=1-0.2754=0.7246
Gain(S,A=”今天心情如何?”)=E(S)−E(S,A=”今天心情如何?”)=1−0.2754=0.7246
因为 0.61 < 0.7246 0.61<0.7246 0.61<0.7246,所以选择“今天心情如何?”作为样本集S的划分特征。接下来,递归调用算法。
ID3算法的优缺点
ID3算法根据信息增益来选择划分属性,该算法的主要优缺点有:
-
优点:
- 模型简单
- 分类速度快
-
缺点:
- 没有剪枝策略,容易过拟合。
- 只能处理离散属性数据。
- 不能处理有缺失的数据。
- 仅是局部最优的决策树:ID3采用贪心算法,结果非全局最优。
- 偏好取值种类多的属性:ID3采用信息增益作为选择分裂属性的度量标准,但大量的研究分析与实际应用发现,信息增益偏向于选择属性值个数较多的属性,而属性取值个数较多的属性并不一定是最优或分类能力最强的属性。例如:以“生日”或“身份证号”作为划分属性。(信息增益很大,但过拟合,预测效果差)
C4.5算法
C4.5算法是对ID3的一个改进,它根据信息增益率来选择划分属性。
主要优点:C4.5 相对于 ID3 的缺点对应有以下改进方式:
- 引入
悲观剪枝策略进行后剪枝; - 引入
信息增益率作为划分标准; - 将
连续特征离散化; 空值(缺失值)处理。
主要缺点:
- 剪枝策略可以再优化;
- 用的是多叉树,用二叉树效率更高;
- 只能用于分类
- 在构造树的过程中,对数值属性值需要按照其大小进行排序,从中选择一个分割点,所以只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时,程序无法运行。
信息增益率
定义:设有限个样本点集合S,根据条件属性A划分S所得子集为
{
S
1
,
S
2
,
…
,
S
v
}
\{S_1,S_2,…,S_v\}
{S1,S2,…,Sv},则定义A划分样本集S的信息增益率为:
G
a
i
n
R
a
t
i
o
(
S
,
A
)
=
G
a
i
n
(
S
,
A
)
/
I
V
(
A
)
GainRatio(S, A)=Gain(S, A)/IV(A)
GainRatio(S,A)=Gain(S,A)/IV(A)
其中,
G
a
i
n
(
S
,
A
)
Gain(S,A)
Gain(S,A)的计算公式见式
G
a
i
n
(
S
,
A
)
=
E
(
S
)
−
E
(
S
,
A
)
Gain(S,A)=E(S)-E(S,A)
Gain(S,A)=E(S)−E(S,A),IV(A)如下:
I
V
(
A
)
=
−
∑
j
=
1
v
∣
S
j
∣
∣
S
∣
l
o
g
2
(
∣
S
j
∣
∣
S
∣
)
IV(A)=-\displaystyle \sum^v_{j=1}\frac{|S_j|}{|S|}log_2(\frac{|S_j|}{|S|})
IV(A)=−j=1∑v∣S∣∣Sj∣log2(∣S∣∣Sj∣)
称为属性A的“固有值”,属性A的取值数目越多,即v越大,则IV(A)的值通常会越大。
需注意的是,增益率准则对可取值数目较少的属性有所偏好。因此,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式[Quinlan,1993]:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
划分选择或划分标准——Gini系数(CART算法)
-
Gini系数又称为基尼系数或者基尼指数
-
Gini系数的小故事:1905年,统计学家洛伦茨提出了洛伦茨曲线。为了用指数来更好的反映社会收入分配的平等状况,1912年,意大利经济学家基尼根据洛伦茨曲线计算出一个反映收入分配平等程度的指标,称为基尼系数G。
-
图中横轴是人口比例的累积分布,竖轴是财富比例的累积分布。

Gini系数的定义: -
CART算法采用Gini系数来衡量结点的
不纯度,如果某个结点所包含的样本集均属于同一个类别,则该结点就是“纯”的,其Gini系数=0。 -
定义:设有限个样本点集合S,分类属性C={C1, C2,…, Ck}。假设当前样本集合S中第i类(即Ci)样本所占的比例(或称其为概率)为pi(i=1,2,…,k),则衡量S纯度的基尼系数为:

-
Gini系数越小,数据集S的纯度越高。
如果要使用属性A来划分数据集S,且划分为两部分(因为CART算法要求决策树为二叉树),则需要确定选择何种二元划分方式来构造分支。假设属性A有v个可能的取值 { a 1 , a 2 , … , a v } \{a_1, a_2, …, a_v\} {a1,a2,…,av},从中选择第 i i i个值 a i a_i ai作为划分标准,即该分支所对应的判别条件分别为 A = a i , A ≠ a i A=a_i,A \neq a_i A=ai,A=ai。根据这两个判别条件可将S划分为两个子集 S 1 S_1 S1和 S 2 S_2 S2,该划分所对应的基尼系数为:
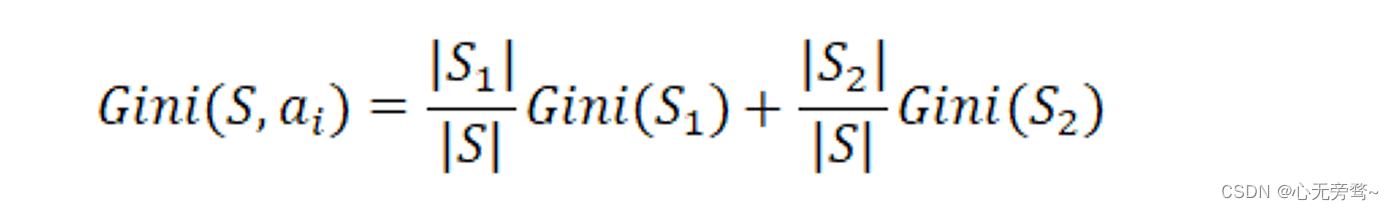
也即集合S在属性A取值为
a
i
a_i
ai的情况下,集合S的基尼系数。其中,i=1,2,…,v。
Gini系数计算举例
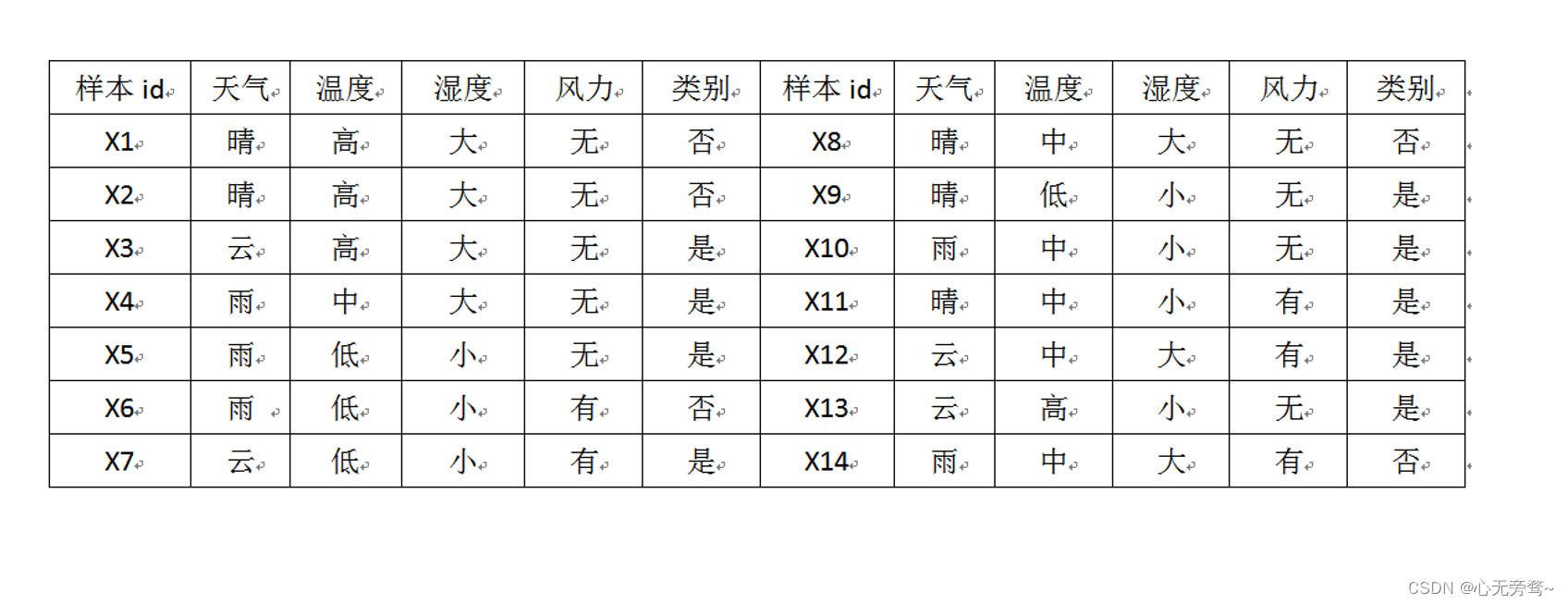
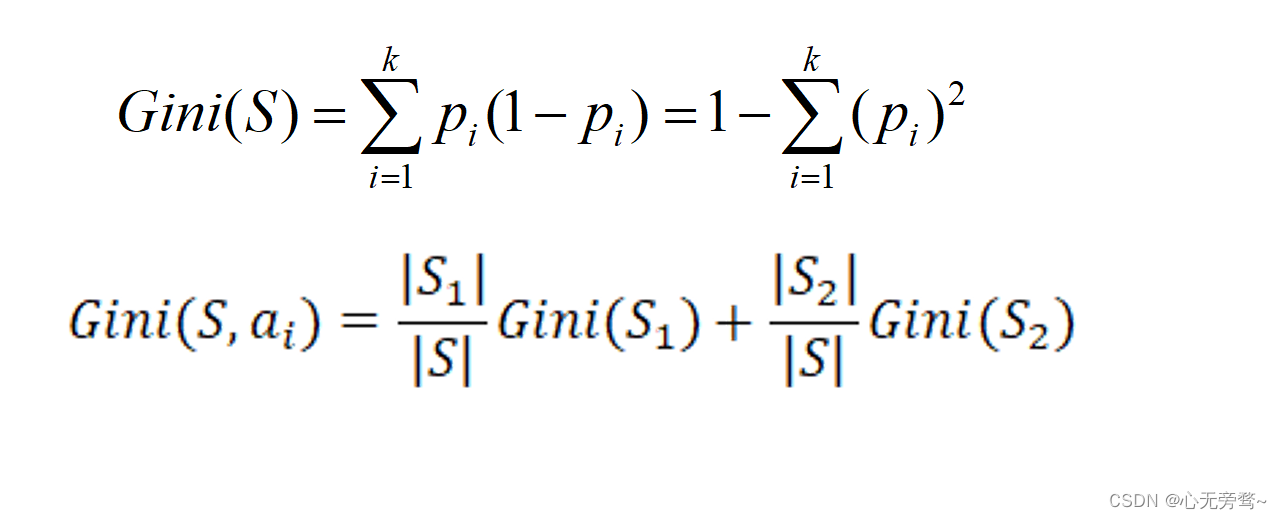
CART算法的优缺点
-
CART树是根据Gini系数来衡量结点的不纯度,选择产生最小Gini系数的特征作为划分属性。
-
主要优点:ID3 和 C4.5 虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但是其生成的决策树分支、规模都比较大,CART 算法的二分法可以简化决策树的规模,提高生成决策树的效率。
-
CART使用Gini系数作为变量的不纯度量,减少了大量的对数运算;
-
CART包含的基本过程有分裂,剪枝和树选择。
- 分裂:分裂过程是一个二叉递归划分过程,其输入和预测特征既可以是连续型的也可以是离散型的,CART没有停止准则,会一直生长下去;
- 剪枝:采用“基于代价复杂度剪枝”方法进行剪枝,从最大树开始,每次选择训练数据熵对整体性能贡献最小的那个分裂结点作为下一个剪枝对象,直到只剩下根结点。CART 会产生一系列嵌套的剪枝树,从中选出一颗最优的决策树;
- 树选择:用单独的测试集评估每棵剪枝树的预测性能(也可以用交叉验证)。
-
CART在C4.5的基础上进行了很多提升,例如:
- C4.5为多叉树,运算速度慢;CART为二叉树,运算速度快;
- C4.5只能分类,CART既可以分类也可以回归;
- CART采用代理测试来估计缺失值,而C4.5以不同概率划分到不同节点中;
- CART采用“基于代价复杂度剪枝”方法进行剪枝,而C4.5采用悲观剪枝方法。
其他比较
(1)划分标准的差异:ID3使用信息增益偏向特征值多的特征;C4.5使用信息增益率克服信息增益的缺点,偏向于特征值小的特征;CART使用基尼指数克服C4.5需要求log的巨大计算量,偏向于特征值较多的特征。
(2)使用场景的差异:ID3和C4.5都只能用于分类问题,CART可以用于分类和回归问题;ID3和C4.5是多叉树,速度较慢,CART是二叉树,计算速度很快;
(3)样本数据的差异:ID3只能处理离散数据且缺失值敏感,C4.5和CART可以处理连续性数据且有多种方式处理缺失值;从样本量考虑的话,小样本建议C4.5、大样本建议CART。C4.5处理过程中需对数据集进行多次扫描排序,处理成本耗时较高,而CART本身是一种大样本的统计方法,小样本处理下泛化误差较大;
(4)样本特征的差异:ID3和C4.5层级之间只使用一次特征,CART可多次重复使用特征;
(5)剪枝策略的差异:ID3没有剪枝策略,C4.5是通过悲观剪枝策略来修正树的准确性,而 CART是通过代价复杂度剪枝。
连续值的处理

还是这张表格,C4.5采用了二分法来处理连续值。
- 步骤1:将训练集中的样本在连续属性A上的取值从小到大排序。假设训练样本集中属性A有v个不同的取值,按非递减方式排序结果记为 { a 1 , a 2 , … , a v } \{a_1,a_2,…,a_v\} {a1,a2,…,av};
- 步骤2:按照顺序将两个相邻的平均值 a a v g = a i + a i + 1 2 ( i = 1 , 2 , . . . , v − 1 ) a^{avg}=\frac{a_i+a_{i+1}}{2}(i=1,2,...,v-1) aavg=2ai+ai+1(i=1,2,...,v−1)作为分割点,共获得v-1个分割点,且每个分割点都将样本集划分为两个子集,分别包含在A上取值 ≤ a a v g \leq a^{avg} ≤aavg和 > a a v g >a^{avg} >aavg的样本。
- 步骤3:计算v-1个分割点划分样本集的信息增益,选择具有
最大信息增益的分割点 v ′ v' v′,将样本集划分为 A ≤ v ′ A\leq v' A≤v′和 A > v ′ A>v' A>v′两个子集。(CART算法选择具有最小Gini系数的分割点)
ID3和C4.5的结果比较
采用C4.5算法,经过计算,以87.5为分割点时信息增益最大。因此将湿度87.5及其以下数据标记为湿度“小”,反之标记为湿度“大”。
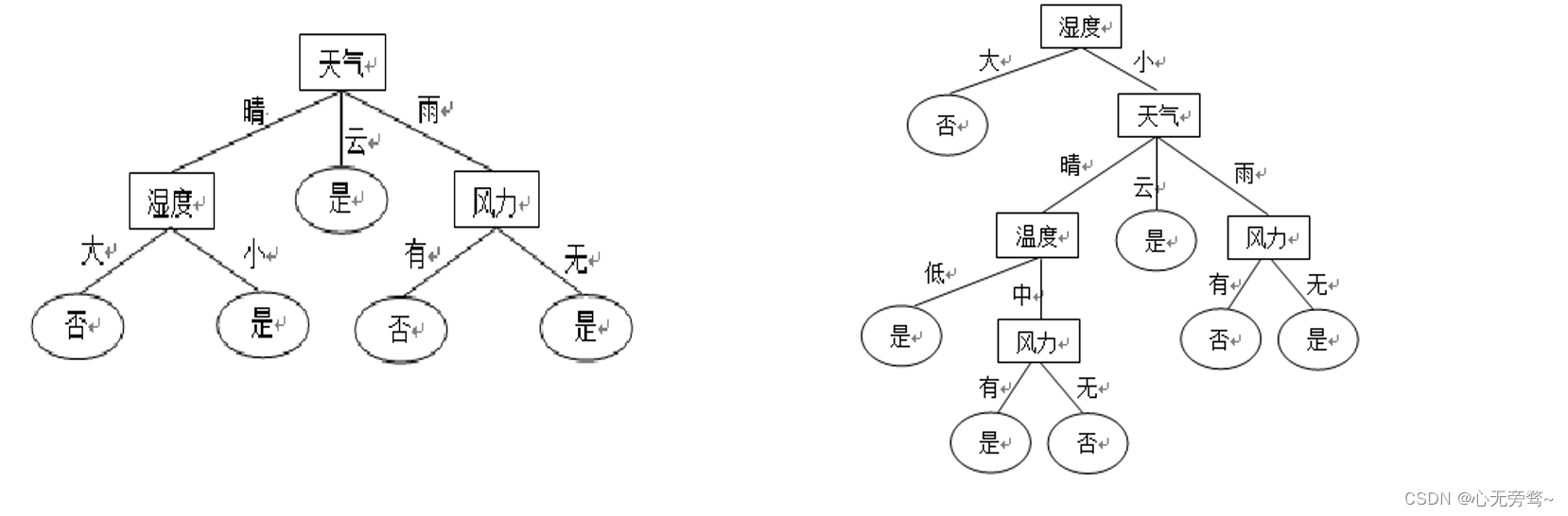
连续属性的离散化方法是否合理,直接影响C4.5生成的决策树质量以及所生成的分类规则质量。
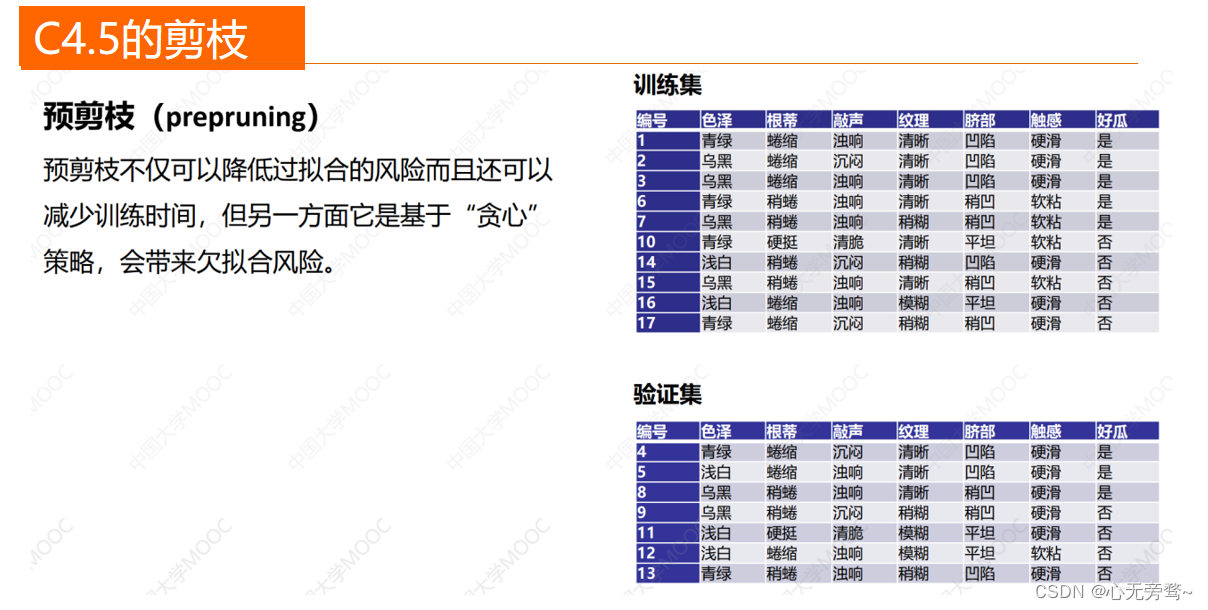
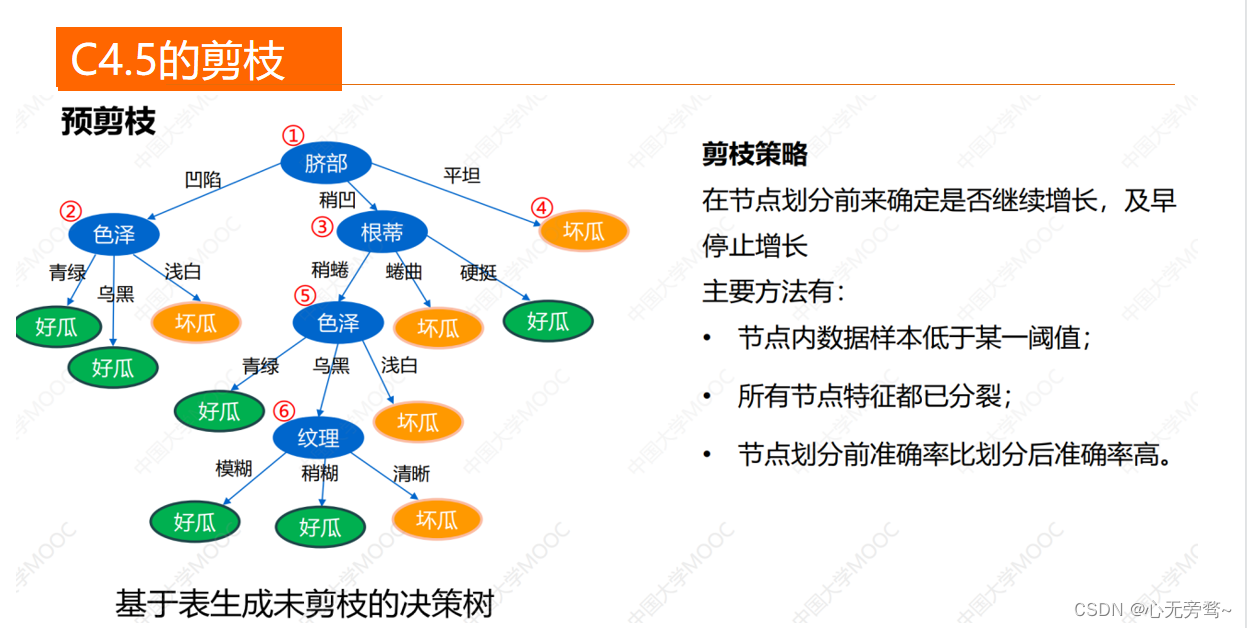
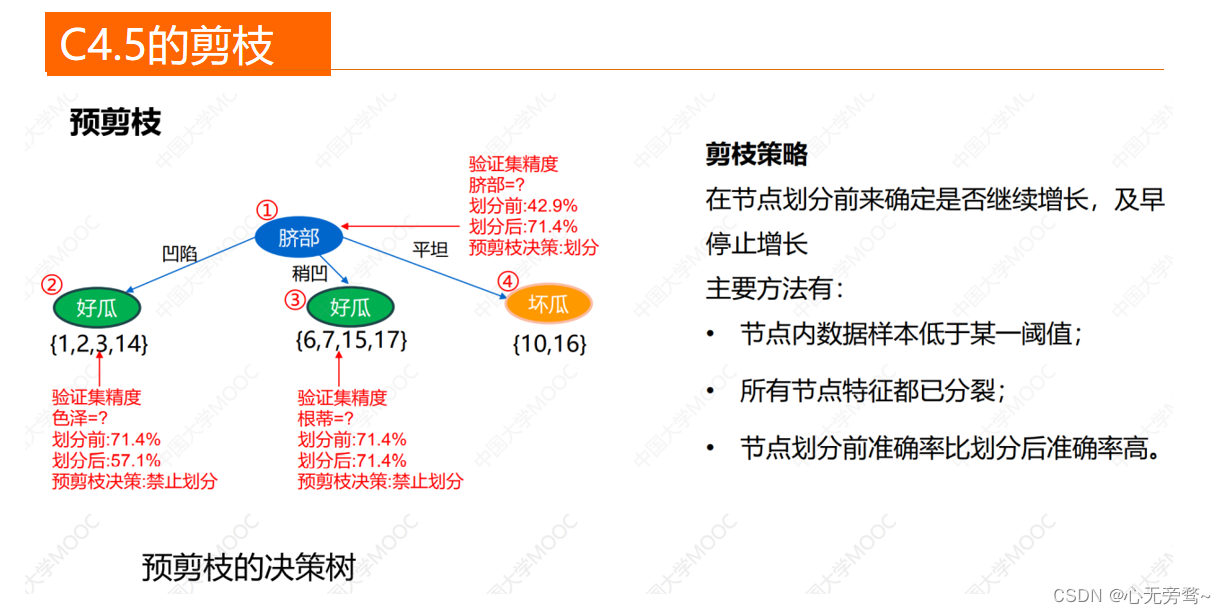
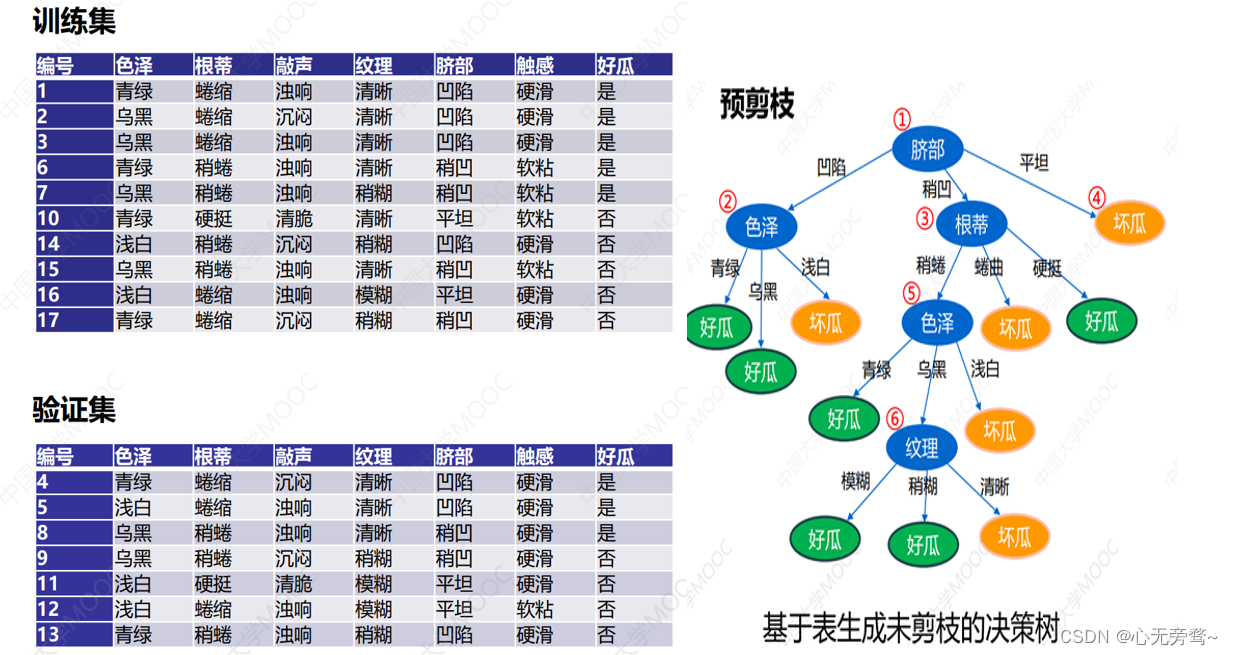
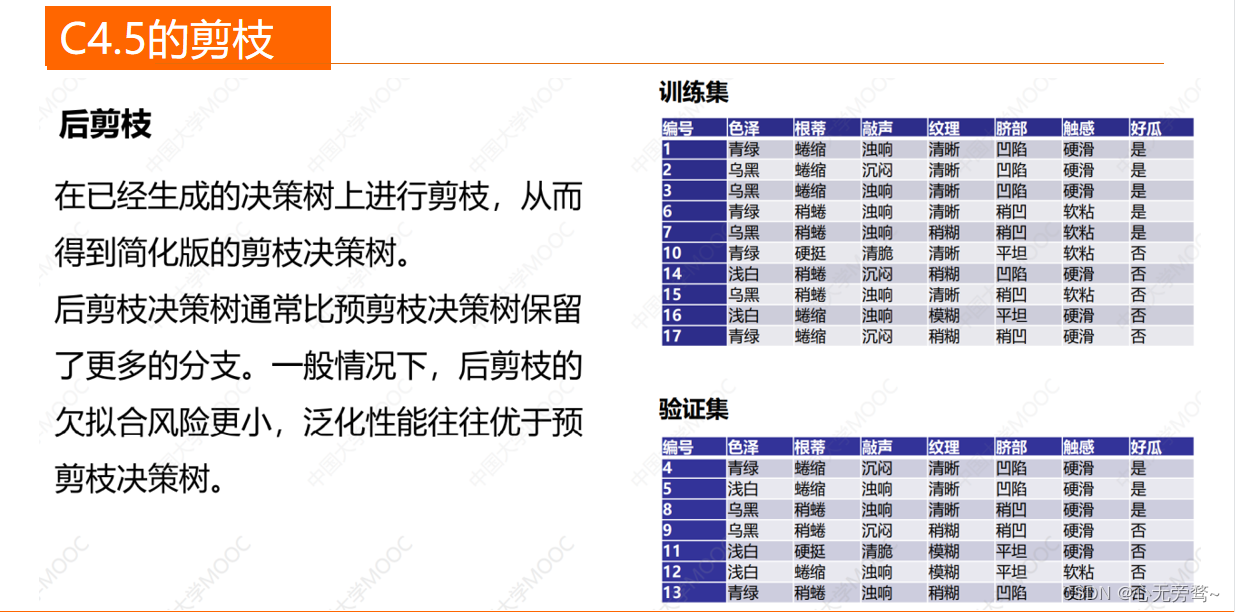
C4.5的剪枝
过拟合原因:
为了尽可能正确分类训练样本,节点的划分过程会不断重复直到不能再分,这样就可能对训练样本学习的“太好”了,把训练样本的一些特点当做所有数据都具有的一般性质,从而导致过拟合。
解决办法:通过剪枝处理去掉一些分支来降低过拟合的风险。
剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(post-pruning)。
Python实现案例
案例1:鸢尾花Iris数据集
莺尾花数据集介绍:

鸢尾花数据集是一类多重变量分析的数据集,常用于分类实验。该数据集由150个数据样本组成,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。其它比较流行的数据集还有Adult,Wine,Car Evaluation等。
鸢尾花数据集的特点是包含了4个属性:sepal.length(花萼长度),sepal.width(花萼宽度)和petal.length(花瓣长度)和petal.width(花瓣宽度)。这些属性可以用来预测鸢尾花卉属于哪个种类。此外,鸢尾花数据集还包含了3个线性可分离的特征:sepal.Length-Petal.Width(花萼长度-花瓣宽度),sepal.Length-Sepal.Width(花萼长度-花萼宽度)和sepal.Length-Petal.Length(花萼长度-花瓣长度)。
鸢尾花数据集常用于分类实验,因为它可以提供多个有用的特征来区分不同的种类。在使用鸢尾花数据集时,需要注意的是,该数据集只包含了3个种类,因此如果需要进行更复杂的分类任务,可能需要使用其他数据集或方法。
代码实现:
import numpy as np
from sklearn.tree import DecisionTreeClassifier
import sklearn.datasets as datasets
from sklearn.model_selection import train_test_split
iris=datasets.load_iris()
print(iris['target_names'])
X=iris['data']
y=iris['target']
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
clf=DecisionTreeClassifier(max_depth=1)
clf.fit(X_train,y_train) #训练模型
print(clf.score(X_test,y_test))#预测模型,等价于下面两行代码
#y_t=clf.predict(X_test)
#print((y_t==y_test).mean())
X_new=np.array([[0.6,0.34,0.5,0.55]])
y_new=clf.predict(X_new)#预测新样本
print(iris['target_names'][y_new])
# 输出结果:
['setosa' 'versicolor' 'virginica']
1.0
['setosa']
上述我们使用clf=DecisionTreeClassifier()函数的时候设置参数max_depth=1,其实DecisionTreeClassifier是一个用于构建决策树模型的Python库。以下是该函数的参数解释:
- criterion(标准化度量):指定使用哪种标准化度量方法,可选值包括“entropy”(信息熵)和“gini”(基尼系数)。默认值为“entropy”。
- min_samples_leaf(叶子节点最小样本数):如果一个叶子节点的样本数小于这个值,则将其视为噪声点,并在训练集中删除。默认值为3。
- max_depth(最大深度):指定决策树中的最大深度。深度越大,越容易过拟合,推荐树的深度为5-20之间。默认值为None。
- random_state(随机种子):用于生成均匀分布的随机数。如果不提供,则会使用当前时间作为随机种子。默认值为None。
如果我们将上述函数的参数设置为2,即clf=DecisionTreeClassifier(max_depth=2),那么预测的精度就会发生改变,这是由于树的深度越大,越容易发生过拟合。也就是我们上面所说的,下面我们看下设置为参数设置为2的时候的精度变化。
import numpy as np
from sklearn.tree import DecisionTreeClassifier
import sklearn.datasets as datasets
from sklearn.model_selection import train_test_split
iris=datasets.load_iris()
print(iris['target_names'])
X=iris['data']
y=iris['target']
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=0)
clf=DecisionTreeClassifier(max_depth=2)
clf.fit(X_train,y_train) #训练模型
print(clf.score(X_test,y_test))#预测模型,等价于下面两行代码
#y_t=clf.predict(X_test)
#print((y_t==y_test).mean())
X_new=np.array([[0.6,0.34,0.5,0.55]])
y_new=clf.predict(X_new)#预测新样本
print(iris['target_names'][y_new])
# 结果如下:
['setosa' 'versicolor' 'virginica']
0.9666666666666667
['setosa']
如果我们继续实验下去会发现,当参数设置为5的时候,那么预测的score就是高达1,那么很有可能就会发生过拟合。所以我们预测的时候参数要设置到合适的值。
决策树的可视化
好奇:决策树在每一层都做了哪些事情?
在学习使用scikitlearn的决策树方法时候,会产生一个dot格式的文件来表示最终的结果。我想把这个dot树可视化,也即可视化决策树的工作过程。
- 可视化方法1:安装graphviz库。不同于一般的Python包,graphviz需要额外下载可执行文件,并配置环境变量。
- 可视化方法2:安装pydotplus包也可以。
【代码展示】在prompt里,输入pip install pydotplus。联网安装pydotplus,可视化决策树的工作过程。
#剪枝案例
# -*- coding: utf-8 -*-
from sklearn.datasets import load_iris
from sklearn import tree
import numpy as np
import pydotplus
#from sklearn.externals.six import StringIO
from six import StringIO #StringIO模块实现在内存缓冲区中读写数据
import pydotplus
#----------------数据准备----------------------------
iris = load_iris() # 加载数据
X = iris.data
y = iris.target
#---------------模型训练---------------------------------
clf = tree.DecisionTreeClassifier(min_samples_split=10,ccp_alpha=0)
clf = clf.fit(X, y)
#-------计算ccp路径-----------------------
pruning_path = clf.cost_complexity_pruning_path(X, y)
#-------打印结果---------------------------
print("\n====CCP路径=================")
print("ccp_alphas:",pruning_path['ccp_alphas'])
print("impurities:",pruning_path['impurities'])
# 输出如下:
====CCP路径=================
ccp_alphas: [0. 0.00415459 0.01305556 0.02966049 0.25979603 0.33333333]
impurities: [0.02666667 0.03082126 0.04387681 0.07353731 0.33333333 0.66666667]
对以上输出的解释如下:
0<α<0.00415时,树的不纯度为 0.02666,0.00415< α<0.01305时,树的不纯度为 0.03082,0.01305<α<0.02966时,树的不纯度为 0.04387,…其中,树的不纯度指的是损失函数的前部分, 也即所有叶子的不纯度(gini或者熵)加权和。
ccp_path只提供树的不纯度,如果还需要alpha对应的其它信息,则可以将alpha代入模型中训练,从训练好的模型中获取。
根据树的质量,选定alpha进行剪树. 我们根据业务实际情况,选择一个可以接受的树不纯度,找到对应的alpha,例如,我们可接受的树不纯度为0.0735,
则alpha可设为0.1(在0.02966与0.25979之间)对模型重新以参数ccp_alpha=0.1进行训练,即可得到剪枝后的决策树。
#------设置alpha对树后剪枝-----------------------
clf = tree.DecisionTreeClassifier(min_samples_split=10,random_state=0,ccp_alpha=0.1)
clf = clf.fit(X, y)
#------自行计算树纯度以验证-----------------------
is_leaf =clf.tree_.children_left ==-1
tree_impurities = (clf.tree_.impurity[is_leaf]* clf.tree_.n_node_samples[is_leaf]/len(y)).sum()
#-------打印结果---------------------------
print("\n==设置alpha=0.1剪枝后的树纯度:=========\n",tree_impurities)
# 输出结果如下:
==设置alpha=0.1剪枝后的树纯度:=========
0.0735373054213634
dot_data = StringIO()
print(type(dot_data))
file_name=r"iris2.dot" # 路径自己设置
tree.export_graphviz(clf, out_file=file_name,
feature_names=iris.feature_names,
class_names=iris.target_names, #filled:布尔,默认=假。当设置为 True 时,绘制节点以指示分类的多数类、回归值的极值或 multi-output 的节点纯度。
filled=True, rounded=True, #rounded:布尔,默认=假,当设置为 True 时,绘制圆角节点框。
special_characters=True) #此函数生成决策树的 GraphViz 表示,然后将其写入 out_file
with open(file_name)as f:
dot_graph=(type(dot_data))(f.read())
graph = pydotplus.graph_from_dot_data(dot_graph.getvalue())#决策树可视化
print(dot_graph)
graph.write_pdf(r'iris2.pdf') # # 路径自己设置
结果如下:
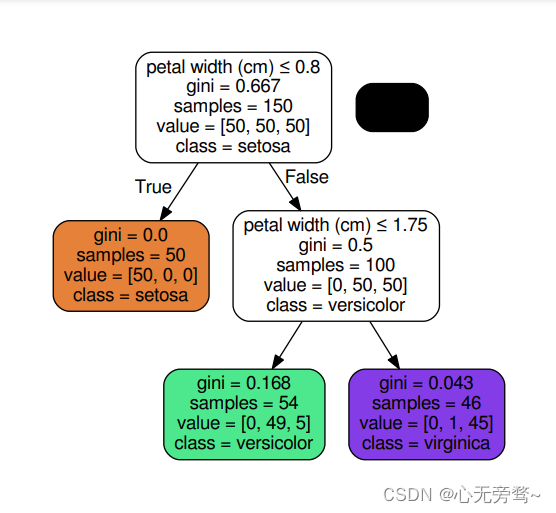
✨ 原创不易,还希望各位大佬支持一下 \textcolor{blue}{原创不易,还希望各位大佬支持一下} 原创不易,还希望各位大佬支持一下
👍 点赞,你的认可是我创作的动力! \textcolor{green}{点赞,你的认可是我创作的动力!} 点赞,你的认可是我创作的动力!
⭐️ 收藏,你的青睐是我努力的方向! \textcolor{green}{收藏,你的青睐是我努力的方向!} 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富! \textcolor{green}{评论,你的意见是我进步的财富!} 评论,你的意见是我进步的财富!
