C语言数据结构初阶(8)----栈与队列OJ题
· CSDN的uu们,大家好。这里是C语言数据结构的第八讲。
· 目标:前路坎坷,披荆斩棘,扶摇直上。
· 博客主页: @姬如祎
· 收录专栏: 数据结构与算法

栈与队列的知识
点我 ➡ ➡ 队列相关
点我 ➡ ➡ 栈相关
2. 用栈实现队列
原题链接:
剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode)
232. 用栈实现队列 - 力扣(Leetcode)
题目描述:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push 、pop 、peek 、empty ):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
2.1 思路分析
一个队列里面包含了两个栈,stack1和stack2。直讲解有点抽象,我们用一个具体的例子来讲解。
假设我们要向队列中插入,1,2,3三个元素后将它们删除,如何实现呢?
首先,我们插入1这个元素,不妨把他插入到stack1,然后再依次插入,2,3,此时stack1内栈顶元素为3,stack2为空(见下图)。
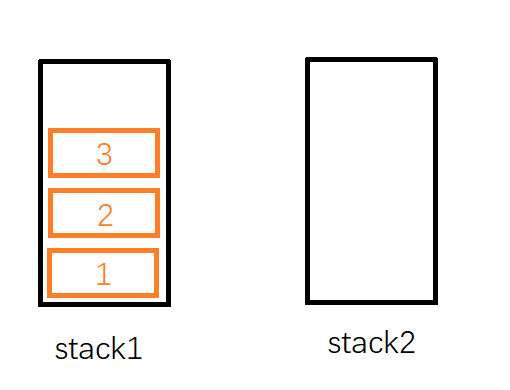
这时候,我们尝试从队列中删除一个元素。按照队列先入先出的规则,最先入列的1应该是最先出列的,故应该删除1。但是1存储在stack1中并不是在栈顶,于是我们需要借助stack2:如果我们把stack1中的元素依次弹出,并压入到stack2中,则stack2中的元素顺序正好和原来相反。因此经过三次弹出stack1和压入stack2的操作后,stack1为空,stack2中的元素是 3, 2, 1,这时候就可以弹出栈顶的1了。
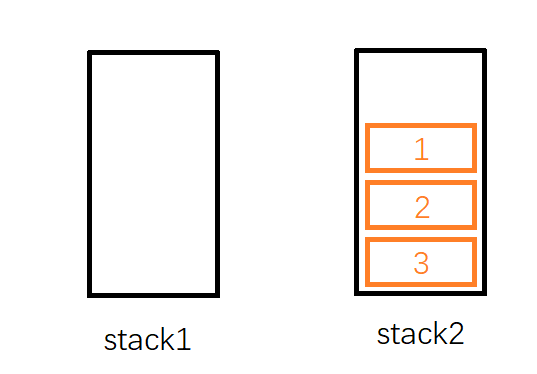
在删除队头的1后,队列中还剩2和3,我们想要继续删除队头的元素,那么应该删除2,而此时2恰好又在栈顶,因此直接弹出2即可。
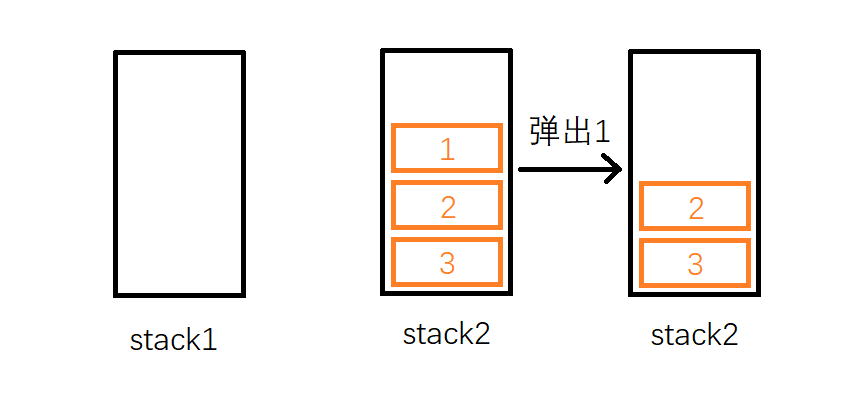
通过例子的分析我们就可以总结如下规律:
添加元素的步骤:直接将元素入栈到stack1即可。
删除元素的步骤:当stack2不为空时,在栈顶的元素就是队列中先入列的元素,直接弹出栈顶的元素即可;当stack2为空时,我们就需要将stack1中的元素依次弹出并压入到stack2中,直到stack1为空。如果说stack2为空,去stack1中拿元素时发现stack1也为空,根据题目要求返回-1即可。
销毁队列:销毁两个栈即可。
当然你也可以用数组模拟实现栈,进而用两个栈实现队列。
2.2 代码实现
#define INIT_STACK_SIZE 4
typedef char STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
} ST;
void StackInit(ST* st)
{
assert(st);
st->a = (STDataType*)malloc(sizeof(STDataType) * INIT_STACK_SIZE);
st->capacity = INIT_STACK_SIZE;
st->top = 0;
}
void StackPush(ST* st, STDataType x)
{
assert(st);
if (st->top == st->capacity)
{
STDataType* new = (STDataType*)realloc(st->a, sizeof(STDataType) * st->capacity * 2);
if (!new)
{
perror("StackPush::malloc");
exit(-1);
}
else
{
st->a = new;
st->capacity *= 2;
}
}
st->a[st->top] = x;
st->top++;
}
void StackPop(ST* st)
{
assert(st);
assert(st->top);
st->top--;
}
bool StackEmpty(ST* st)
{
assert(st);
return st->top == 0;
}
STDataType StackTop(ST* st)
{
assert(st);
assert(st->top);
return st->a[st->top - 1];
}
int StackSize(ST* st)
{
assert(st);
return st->top;
}
void StackDestory(ST* st)
{
assert(st);
free(st->a);
st->a = NULL;
st->capacity = 0;
st->top = 0;
}
typedef struct {
ST pushStack;
ST popStack;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* queue = (MyQueue*)malloc(sizeof(MyQueue));
StackInit(&queue->pushStack);
StackInit(&queue->popStack);
return queue;
}
void myQueuePush(MyQueue* obj, int x) {
StackPush(&obj->pushStack, x);
}
int myQueuePop(MyQueue* obj) {
if(StackEmpty(&obj->popStack))
{
while(!StackEmpty(&obj->pushStack))
{
StackPush(&obj->popStack, StackTop(&obj->pushStack));
StackPop(&obj->pushStack);
}
}
STDataType top = StackTop(&obj->popStack);
StackPop(&obj->popStack);
return top;
}
int myQueuePeek(MyQueue* obj) {
if(StackEmpty(&obj->popStack))
{
while(!StackEmpty(&obj->pushStack))
{
StackPush(&obj->popStack, StackTop(&obj->pushStack));
StackPop(&obj->pushStack);
}
}
return StackTop(&obj->popStack);
}
bool myQueueEmpty(MyQueue* obj) {
return StackEmpty(&obj->popStack) && StackEmpty(&obj->pushStack);
}
void myQueueFree(MyQueue* obj) {
StackDestory(&obj->pushStack);
StackDestory(&obj->popStack);
free(obj);
}
3. 用队列实现栈
原题链接:
225. 用队列实现栈 - 力扣(Leetcode)
题目描述:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push 、top 、pop 和 empty )。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
3.1 思路分析
一个栈里面包含了两个队列,Queue1和Queue2,直接讲解也是有点抽象,我们通过例子来讲解:
假设我们要依次入栈1, 2,3
首先入栈元素1,同样,我们不妨直接把他插入Queue1中,然后再次插入2, 3到Queue1中,此时Queue1中有三个元素1, 2, 3,Queue2为空。
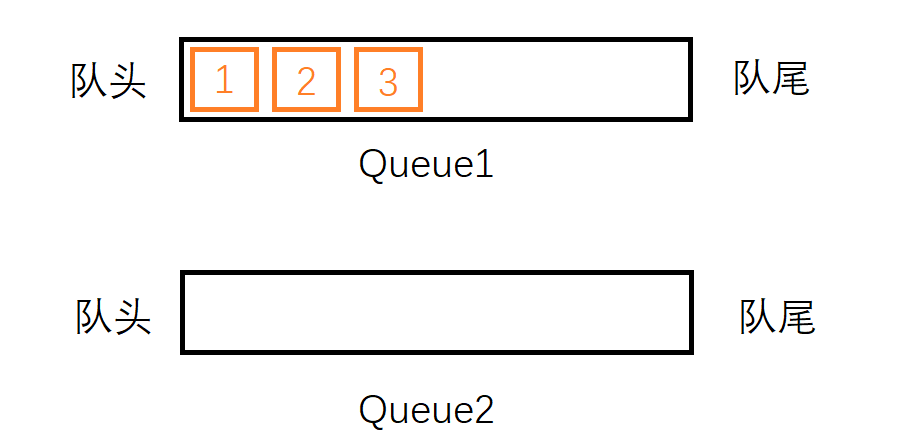
现在,我们尝试从栈中删除一个元素。按照栈后进先出的规则,最后入栈的元素3应该最先出栈。但是元素3并不在Queue1的队头,我们不能直接把他删除。这时候我们就要借助Queue2了:将元素1从Queue1中出列,将它入列到Queue2中;将元素2从Queue1中出列将它入列到Queue2中,此时我们会发现,要出栈的元素3就在Queue1的队头了,直接将其出列即可。
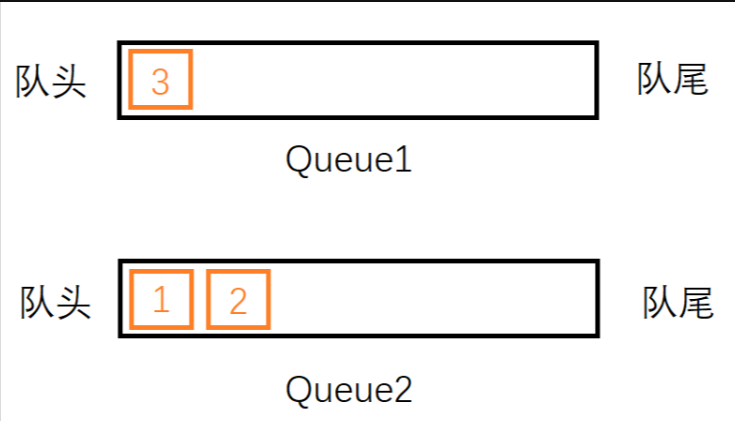
同样地,我们还想删除一个元素,此时2就是栈顶元素,它不在Queue2的队头不能直接删除,同样需要借助另一个队列Queue1,将元素1从Queue2中出列,入列到Queue1中,此时要出栈的元素2,就在Queue2的队头了,直接删除即可。
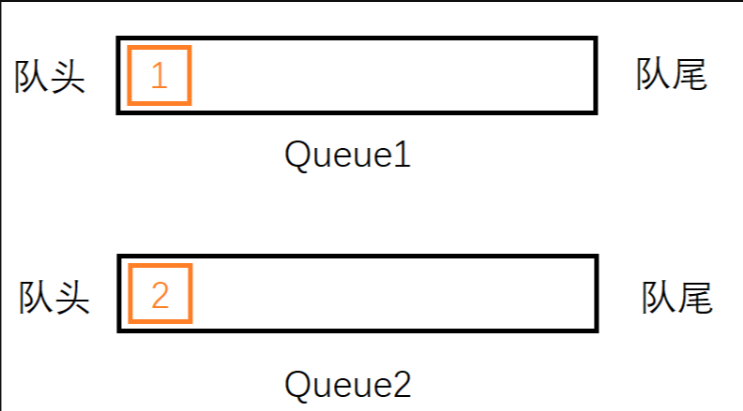
还想删除栈顶的元素1时,我们发现它就在Queue1的队头直接删除即可。
通过以上分析我们总结出一下规律:
删除元素:将不为空的那个队列数据的N-1(N为不为空的那个队列的元素个数/队列大小)个导入到为空的那个队列,剩下的那个元素即为栈顶元素,删除即可。
添加元素:将元素添加到那个不为空的队列中即可,如果两个都为空,随便添加到哪一个都行。
查看栈顶的元素:根据以上分析:不为空的那个队列队尾的数据就是栈顶的元素,我们直接查看队尾的元素即可。
判断栈是否为空:如果两个队列都为空,则栈为空,否则栈不为空。
销毁栈:销毁两个队列即可。
同样地,你也可以使用两个数组来模拟两个队列,进而模拟实现栈。
3.2 代码实现
typedef int QueueDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QueueDataType data;
} QueueNode;
typedef struct Queue
{
QueueNode* head;
QueueNode* tail;
int size;
} Queue;
//队列的初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
//队列的销毁
void QueueDestory(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
while (cur)
{
QueueNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
//队尾增加元素
void QueuePush(Queue* pq, QueueDataType x)
{
assert(pq);
QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
newNode->data = x;
newNode->next = NULL;
if (!pq->head)
{
pq->head = pq->tail = newNode;
}
else
{
pq->tail->next = newNode;
pq->tail = newNode;
}
pq->size++;
}
//队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
//one way
//return pq->size == 0;
//another way
return pq->head == NULL;
}
//出队列
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
//one possibility
//if (pq->head == pq->tail)
//{
// free(pq->head);
// pq->head = pq->tail = NULL;
//}
//else
//{
// QueueNode* next = pq->head->next;
// free(pq->head);
// pq->head = next;
//}
//pq->size--;
//another way
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
pq->size--;
if (pq->head == NULL)
pq->tail = NULL;
}
//队列的元素个数
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
//队头元素
QueueDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
//队尾元素
QueueDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
typedef struct {
Queue q1;
Queue q2;
} MyStack;
MyStack* myStackCreate() {
MyStack* stack = (MyStack*)malloc(sizeof(MyStack));
QueueInit(&stack->q1);
QueueInit(&stack->q2);
return stack;
}
bool myStackEmpty(MyStack* obj) {
return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackPush(MyStack* obj, int x) {
Queue* emptyQueue = &obj->q1, *noneEmptyQueue = &obj->q2;
if(QueueEmpty(&obj->q2))
{
emptyQueue = &obj->q2;
noneEmptyQueue = &obj->q1;
}
QueuePush(noneEmptyQueue, x);
}
int myStackPop(MyStack* obj) {
Queue* emptyQueue = &obj->q1, *noneEmptyQueue = &obj->q2;
if(QueueEmpty(&obj->q2))
{
emptyQueue = &obj->q2;
noneEmptyQueue = &obj->q1;
}
while(QueueSize(noneEmptyQueue) > 1)
{
QueueDataType front = QueueFront(noneEmptyQueue);
QueuePop(noneEmptyQueue);
QueuePush(emptyQueue, front);
}
QueueDataType front = QueueFront(noneEmptyQueue);
QueuePop(noneEmptyQueue);
return front;
}
int myStackTop(MyStack* obj) {
Queue* emptyQueue = &obj->q1, *noneEmptyQueue = &obj->q2;
if(QueueEmpty(&obj->q2))
{
emptyQueue = &obj->q2;
noneEmptyQueue = &obj->q1;
}
return QueueBack(noneEmptyQueue);
}
void myStackFree(MyStack* obj) {
QueueDestory(&obj->q1);
QueueDestory(&obj->q2);
free(obj);
}
4. 有效的括号
原题链接:
20. 有效的括号 - 力扣(Leetcode)
题目描述:
给定一个只包括 '(' ,')' ,'{' ,'}' ,'[' ,']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
4.1 思路分析
你可能会想到用括号的数量来进行判断,但是因为题目要求每个括号都应该与对应的括号进行匹配,这种思路显然是行不通的。
那我们该怎么做呢?大致思路:我们维护一个栈,然后遍历所有的括号,如果说遇到左括号我们就把它入栈。随后继续遍历,如果遇到右括号,我们就取栈顶元素出来,与遍历到的括号类型进行匹配,如果说与栈顶的括号类型不匹配,就返回flase,如果匹配呢?就继续往下遍历。最后判断一下栈是否为空即可。如果说栈为空,所有的左括号均与右括号进行了匹配,返回true,如果栈不为空,说明左括号数量较多,返回false即可!

这里值得注意的是:如果说字符串的一开始就是右括号的类型,那么栈显然就是空,这种情况就需要我们特殊处理一下。
4.2 代码实现
#define INIT_STACK_SIZE 4
typedef char STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
} ST;
void StackInit(ST* st)
{
assert(st);
st->a = (STDataType*)malloc(sizeof(STDataType) * INIT_STACK_SIZE);
st->capacity = INIT_STACK_SIZE;
st->top = 0;
}
void StackPush(ST* st, STDataType x)
{
assert(st);
if (st->top == st->capacity)
{
STDataType* new = (STDataType*)realloc(st->a, sizeof(STDataType) * st->capacity * 2);
if (!new)
{
perror("StackPush::malloc");
exit(-1);
}
else
{
st->a = new;
st->capacity *= 2;
}
}
st->a[st->top] = x;
st->top++;
}
void StackPop(ST* st)
{
assert(st);
assert(st->top);
st->top--;
}
bool StackEmpty(ST* st)
{
assert(st);
return st->top == 0;
}
STDataType StackTop(ST* st)
{
assert(st);
assert(st->top);
return st->a[st->top - 1];
}
int StackSize(ST* st)
{
assert(st);
return st->top;
}
void StackDestory(ST* st)
{
assert(st);
free(st->a);
st->a = NULL;
st->capacity = 0;
st->top = 0;
}
bool isValid(char * s){
if(!s)
return false;
ST st;
StackInit(&st);
int len = strlen(s);
for(int i = 0; i < len; i++)
{
if(s[i] == '(' || s[i] == '[' || s[i] == '{')
StackPush(&st, s[i]);
else
{
if(StackEmpty(&st))
{
StackDestory(&st);
return false;
}
else
{
char top = StackTop(&st);
if(top == '(' && s[i] == ')' || top == '{' && s[i] == '}' || top == '[' && s[i] == ']')
StackPop(&st);
else
{
StackDestory(&st);
return false;
}
}
}
}
bool isEmpty = StackEmpty(&st);
StackDestory(&st);
return isEmpty;
}
5. 设计循环队列
原题链接:
622. 设计循环队列 - 力扣(Leetcode)
题目描述:
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空,返回 -1 。
Rear: 获取队尾元素。如果队列为空,返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。
5.1 循环队列的基础知识
循环队列的定义:我们把队列头尾相接的顺序存储结构称为循环队列。
循环队列的逻辑结构:
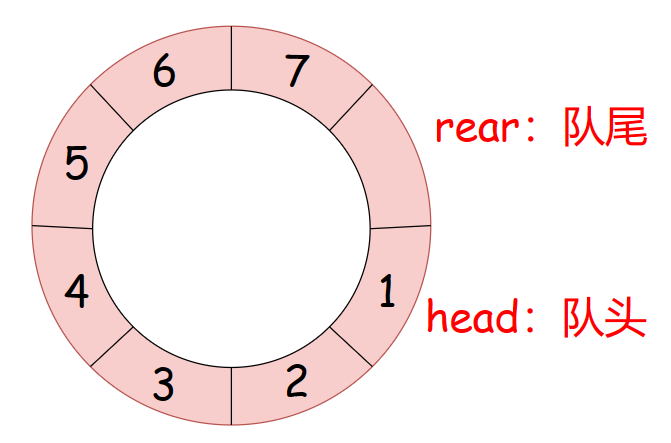
大家可以看到我这里空了一个位置,至于是为什么?有什么作用?我先卖个关子!😊😊
循环队列的缺点:用数组实现的话,队列的容量随着数组定义是就已经确定啦。
循环队列的优点:增加了空间的使用效率。
5.2 数组OR链表
大家一看到循环队列的逻辑结构肯定第一想法就是用链表实现。那么用链表实现行不行呢?当然是没有问题的,但是我们肯定要经过各种比较选择出一种最优秀的方法撒!
无论用什么什么数据结构实现我们都会面临一个问题:怎么判断循环队列是否已经满了嘞?这个点在设计循环队列时是相当重要的。
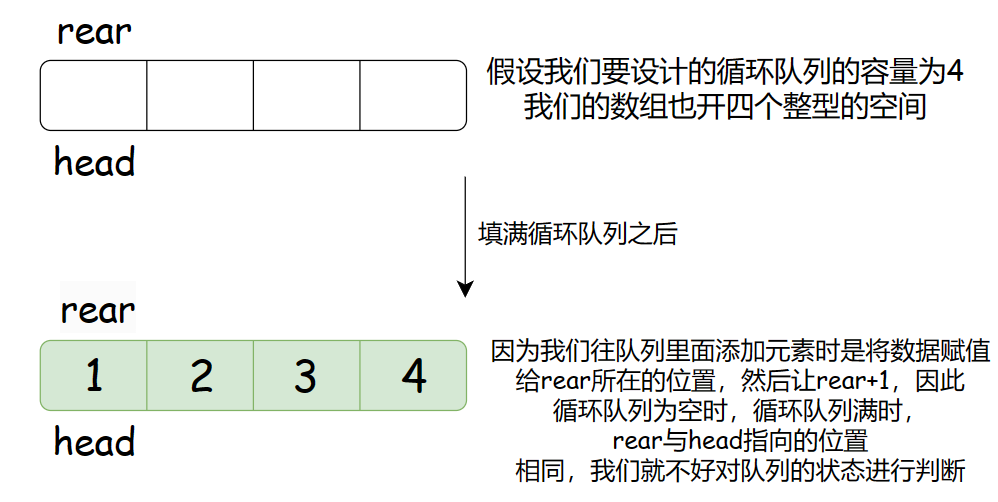
对于链表也是同样的道理。那么我们该怎么解决这个问题呢?你说,我们可以一开始令rear不同head,这样就可以很好的区分循环队列空和满的状态了,或许你也可能会说:我们可以维护一个变量来记录循环队列的大小,这样也能区分循环队列空与满的状态。不错,你很厉害。
但是呢,这里还有一个方法。不妨我们一起来看看:比如我们要设计的循环队列容量为3,我们的数组就开4个整型的大小。这样做也能很好的区分循环队列空与满的状态哦!
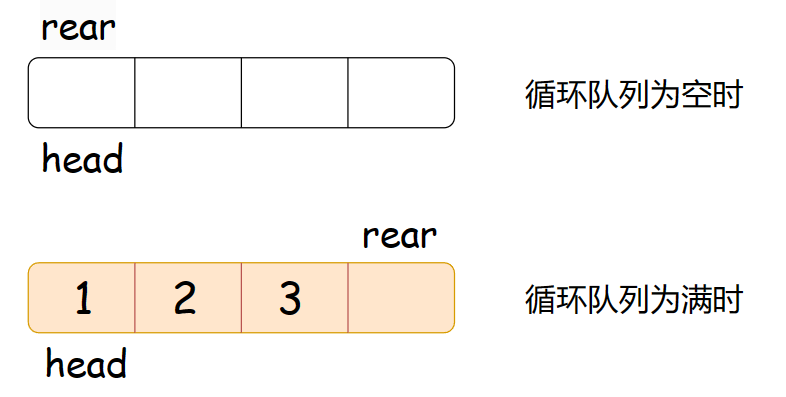
我们看到这样设计的话当rear的下一个位置是head时就是循环队列为满的状态,当head等于rear时就是循环队列为空的时候。链表同理的哈!
那么,到底是哪种方法好呢?仁者见仁智者见智,很多书都是以这种多开一个空间的方式来设计循环队列的,我们这里就是讲解这种啦!
回到我们的正题:是链表还是数组呢?
我们来看看链表:乍一看好像没啥问题,但是注意到看到题目我们是要实现获取队尾元素的这个函数的,单向的循环链表显然找尾是非常麻烦的。你说,我们可以用双向循环链表呀!很好,没有问题。只是这样做的话,是不是有些复杂呢?
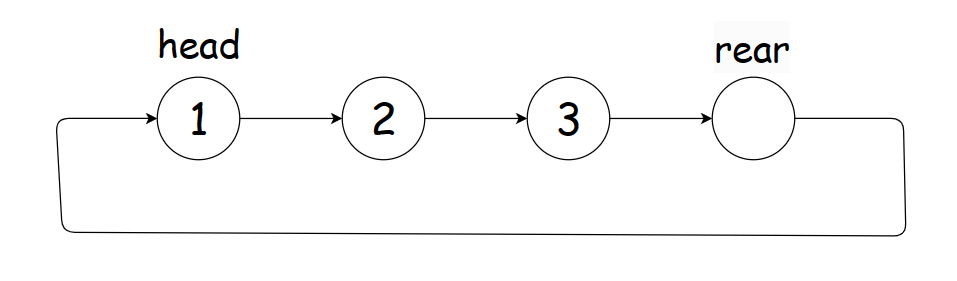
我们来看看数组:取队尾元素我们只要访问rear下标减一的位置就行,只是可能存在数组下标越界的问题,很简单我们只需要在rear加一和rear减一的过程中对结果取模就行啦!
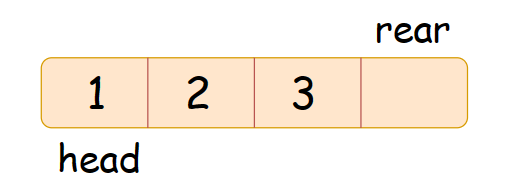
综上所述:设计循环队列我们选用一个比循环队列容量大一的数组来实现。
5.3 函数的实现
因为在操作数据时我们要用到循环队列的容量,还要维护head,rear等变量,所以我们将它们全部封装在一个结构体里面,结构如下:
typedef struct {
int front; //就是上面所有图中的head,表示队头元素
int rear; //队尾元素
int size; //循环队列的容量,这个一开始就是确定了的
int* queue; //设计循环队列的数组
} MyCircularQueue;MyCircularQueue(k): 构造器,设置队列长度为 k 。
这个函数我们需要把数组开辟出来,大小就是循环队列的长度加一。还需要初始化我们维护的变量。
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* q = (MyCircularQueue*)malloc(sizeof(MyCircularQueue)); //开辟结构体
q->front = q->rear = 0; //初始化front和rear
q->size = k; //初始化循环队列的长度
q->queue = (int*)malloc(sizeof(int) * (q->size + 1)); //初始化我们的数组
return q;
}isEmpty(): 检查循环队列是否为空。
这里我们先实现这个函数,因为下面的函数会用到这个函数。根据上面的知识,我们只需要判断rear是不是等于front就可以判断循环队列是不是为空啦!
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front == obj->rear;
}enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
插入元素也比较简单,我们将rear指向的位置进行赋值,然后让rear加一就行啦!只不过需要注意的是rear加一的时候下标可能会越界,这个时候我们就需要对rear加一的值取模。

当然,如果循环队列是满的状态也是不允许插入元素的。
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(((obj->rear + 1) % (obj->size + 1)) == obj->front) //判断循环队列是否为满也需要取模
return false;
else
{
obj->queue[obj->rear] = value;
obj->rear = (obj->rear + 1) % (obj->size + 1);
return true;
}
}
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
删除元素我们只需要让front加一进行逻辑上的删除即可!当然循环队列不为空不允许删除!同时也需要对加一的结果取模!
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return false;
else
{
obj->front = (obj->front + 1) % (obj->size + 1);
return true;
}
}Front: 从队首获取元素。如果队列为空,返回 -1 。
这个函数我们只需要返回front指向的位置就行。当然前提是循环队列不为空啦!
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->queue[obj->front];
}Rear: 获取队尾元素。如果队列为空,返回 -1 。
两个注意点:
1:不为空才能获取队尾元素。
2:因为rear-1才是队尾元素,所以注意取模!
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->queue[(obj->rear - 1 + obj->size + 1) % (obj->size + 1)];
}剩余的函数就不单独写啦!直接放到后面一起的代码实现中啦!
5.4 代码实现
typedef struct {
int front; //就是上面所有图中的head,表示队头元素
int rear; //队尾元素
int size; //循环队列的容量,这个一开始就是确定了的
int* queue; //设计循环队列的数组
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* q = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
q->front = q->rear = 0;
q->size = k;
q->queue = (int*)malloc(sizeof(int) * (q->size + 1));
return q;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front == obj->rear;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(((obj->rear + 1) % (obj->size + 1)) == obj->front)
return false;
else
{
obj->queue[obj->rear] = value;
obj->rear = (obj->rear + 1) % (obj->size + 1);
return true;
}
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return false;
else
{
obj->front = (obj->front + 1) % (obj->size + 1);
return true;
}
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->queue[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->queue[(obj->rear - 1 + obj->size + 1) % (obj->size + 1)];
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return ((obj->rear + 1) % (obj->size + 1)) == obj->front;
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->queue);
free(obj);
}

