当前位置：首页 > article >正文

数组（完全二叉树）向下建堆法与堆排序O(N*logN)

article 2025/1/24 5:26:25

TIPS

AdjustUp & AdjustDown

向上调整AdjustUp与向下调整AdjustDown的参数是一个数组（完全二叉树）+需要进行调整操作的数值的下标/一个数组（完全二叉树）+堆元素个数+需要调整操作的数值的下标。

实际上就是对完全二叉树当中的某一点进行调整直至在其局部范围内满足堆的性质。因此对于完全二叉树如果仅仅对若干个值进行AdjustUp/AdjustDown，并不会是这颗完全二叉树真正变成一个堆。

对于AdjustUp与AdjustDown，在没有任何限制与约束的情况之下，如果说你对数组（完全二叉树）中的某一个元素去进行调整的话，你可以这么做，只不过没有任何意义，因为他最终调整调整，直至在某一个局部范围内满足堆的性质。既然没有任何意义，那它的意义到底是什么呢？AdjustUp与AdjustDown的意义就在于建堆。

那如果说想使用这两个函数往建堆这条正确的方向去走，需要注意：

AdjustUp的前提必须是在child前面数据已经是一个堆；AdjustDown的前提必须是在parent左右两个子树必须是两个堆在这些前提之下，如果说你去AdjustUp与AdjustDown，那么是真正在朝着建堆前进。不然，你在怎么弄的话，只是在局部范围内进行兴风作浪，对于整体并不能使它变成一个堆。

HeapPush & HeapPop

HeapPush与HeapPop的本质与灵魂就是AdjustUp/AdjustDown。这两个的参数分别是一个堆结构体指针+一个需要往堆里面插入的值，一个堆结构体指针。

因此这两个函数的话需要在原先的数组（完全二叉树）就是一个堆的情况下才有意义，不然的话，如果说原先的数组并不是一个堆，那么插入一个数的操作与删除第一个元素意义不大。

数组（完全二叉树）建堆（向下建堆法）O(N)

我们讲过一个建堆方式，就是说是向上调整法建堆，实际上就是不断的插入，如果对于一个数据仅仅进行AdjustUp，只会最终使得局部范围内满足堆的性质，如果说我对数组（完全二叉树）当中的每一个数都进行AdjustUp，那么当我这个操作完了之后，这个数组（完全二叉树）我已经是一个堆了。那有没有其他的方式去建堆呢？

然后我们再进行向下调整法建堆的时候，显而易见的事实就是，我说你对叶子（就是说没有儿子的节点）进行向下调整，那还有什么意义？没有儿子，他调整的也跟白调一样。

所以说向下调整法的话，我需要从倒着往前走，这是第一点（这就为了使得AdjustDown朝着建堆的方向走

并且从倒着往前走之外，我还要从第一个非叶子节点开始进行向下调整。那我该怎么样去找到倒数第一个非叶子节点？我只要把最后一个元素的下标（child）这样（(child-1)/2）找到他父亲不就万事大吉了吗？

为什么要倒着走呢？因为倒着走去向下调整的时候，我就可以确保目前这个节点的左右两个子树都已经是堆，这样子的话，我就确保AdjustDown的能够朝着正确的方向（建堆）前进，而不是一直在局部范围内在兴风作浪。

然后向下调整法建堆的话，它的效率比向上调整法建堆要高且差距极大。一般建堆的话是不会用向上调整建堆。

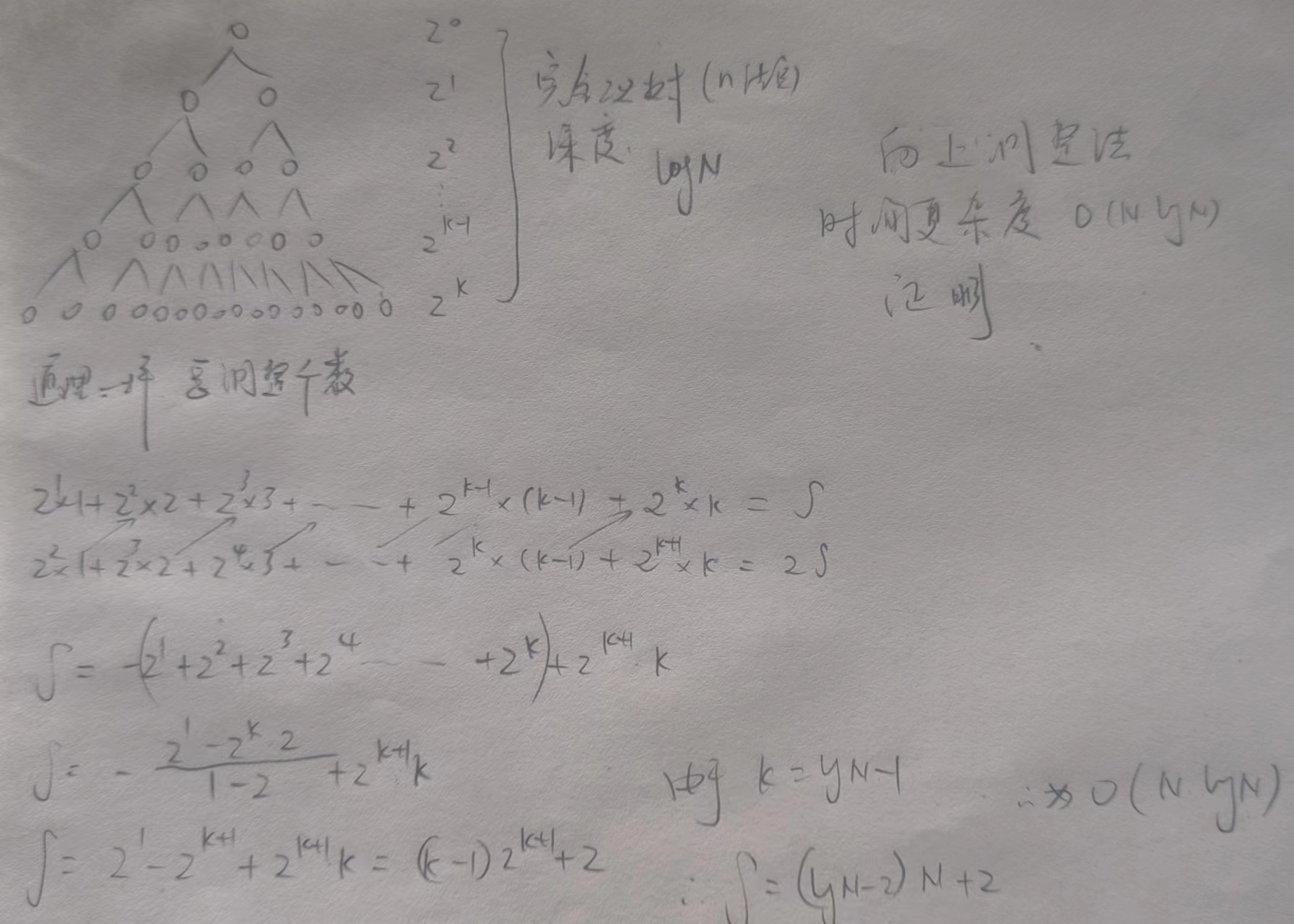
当然，要对数组（完全二叉树）建堆，首先必须得有两个万金油（AdjustUp 与 AdjustDown）

void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void AdjustUp(int* a, int child)
{
    assert(a);
    int parent = (child - 1) / 2;
    while (child > 0)
    {
        if (a[parent] < a[child])
        {
            Swap(a + parent, a + child);
            child = parent;
            parent = (child - 1) / 2;
        }
        else
        {
            break;
        }
    }
}
void AdjustDown(int* a, int parent, int n)
{
    assert(a);
    int child = 2 * parent + 1;
    while (child<n)
    {
        if (child+1 <n && a[child] < a[child + 1])
        {
            child++;
        }
        if (a[parent] < a[child])
        {
            Swap(a + parent, a + child);
            parent = child;
            child = 2 * parent + 1;
        }
        else
        {
            break;
        }
    }
}

演示一下向下调整法建堆

int main()
{
    int arr[15] = { 1,4,5,2,7,8,3,4,9,0,4,3,11,6,8 };
    int size = 15;
    for (int i = (size - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(arr, i, size);
    }
    return 0;
}

建堆的核心就在于把AdjustUp与AdjustDown的核心与意义彻底弄清楚

以后建堆就关注这两个：数组（完全二叉树）得有+AdjustDown核心奥义

堆排序 O(NlogN)

堆在我们这边的优点就是说他已经不像之前那样单独的存储数据，他能够做到帮我们去选数

因此的话，从更加程度而言，它能够帮助我们排序，如果排序的数据量小的话倒还无所谓，我说排序的数据量一大，那么对于性能的要求就非常重要。与我们之前学过的冒泡排序，它的时间复杂度是O(N^2)，对堆排序而言的话，它的时间复杂度是O(NlogN)。这两个差异极大

在堆排序之前的话，需要脑子拎清楚的是，我们现在已经不是在堆着那个结构体里面了，现在我们跟手撕数据结构的那个堆就是说自己手搓的那个堆无关了，现在的话相当于就是对题目中给我的数组（完全二叉树）直接进行建堆然后去进行排序。

首先建堆 [ O(N) 向下调整法 ] 数组得有+AdjustDown核心奥义

要对数组（完全二叉树）建堆如果你要升序排列，就要去建大根堆；如果你要降序排列，要去建小根堆，无论是大根还是小根，然后这个数组的顺序确定是从后往前依次慢慢确定下来的。

建堆的向下调整法前面已经讲了

其次调堆 [堆顶与数组末尾开始去倒] AdjustDown核心奥义

当把堆建完之后，接下来就是要去换数据了，这个过程当中的核心核心成员与利器就是AdjustDown，然后每次使用这个函数的时候都需要注意，当前这个堆的数据数量是多少，是每次都要减1减1的哟。

堆排序时间复杂度

堆排序的话，除了一开始要把原始数据（是数组或者说是完全二叉树）建堆之后，还要去转数据调堆。对于第一步，复杂度是O(N)。

然后调堆的时间复杂度也是logN*N，用错位相减法减减算算也很快的，或者说你用直观的方法去看一下，对于最后一层而言，如果说你想要确定最后一层（堆排序的话，它是确定的顺序是从数组的从后往前慢慢确定下来的），要确定最后一层的话，就需要不断的把堆顶的数据给往下调整，这就相当于就是说节点最多的层数，它需要调整的次数也是最多。

因此对于堆排序而言的话，就是说你在一开始对数组（完全二叉树）建堆的时候，无论是用什么方法去建堆，最后总的堆排序时间复杂度都是O(N*logN)

代码

int main()
{
    int arr[10] = { 1,4,3,5,7,9,8,6,2,0 };
    int size = 10;
    //建堆
    for (int i = (size - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(arr, i, size);
    }
    //调堆
    int end = size - 1;
    while (end > 0)
    {
        Swap(arr + 0, arr + end);
        AdjustDown(arr, 0, end);
        end--;
    }
    return 0;
}

你会发现，在堆排序里面无论是建堆还是调堆，都与AdjustUp无关

查看全文

http://www.kler.cn/a/3456.html