当前位置： 首页 > article >正文

力扣最热一百题——验证二叉搜索树

article 2024/12/25 2:39:55

目录

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

题目描述

示例

提示：

二叉搜索树的要求

解法一：采用中序遍历

中序遍历的定义

为什么二叉搜索树的中序遍历是严格递增的

二叉搜索树（BST）的性质：

中序遍历的结果：

举例：

思路解析

Java写法：

C++写法：

运行时间

时间复杂度和空间复杂度

时间复杂度：

空间复杂度：

解法二：递归遍历

Java写法：

所以正确的Java写法如下

C++写法：

运行时间

时间复杂度和空间复杂度

1. 时间复杂度（Time Complexity）

2. 空间复杂度分析（Space Complexity）

1. 递归栈空间：

2. 二叉树的高度：

3. 所以：

总结

解决方案：

关键点：

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

注：下述题目描述和示例均来自力扣

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左

    子树

    只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例

示例 1：

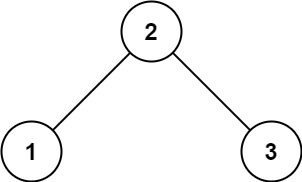
输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

  • 树中节点数目范围在[1, 104] 内
  • -2^{31} <= Node.val <= 2^{31} - 1

二叉搜索树的要求

在二叉搜索树中，任意节点的值都必须满足以下条件：

  • 左子树的所有节点值都小于当前节点的值。
  • 右子树的所有节点值都大于当前节点的值。
  • 左右子树也必须分别满足相同的条件。

解法一：采用中序遍历

中序遍历的定义

中序遍历（Inorder Traversal） 是指按照以下顺序访问二叉树的每个节点：

  • 左子树（递归）
  • 根节点
  • 右子树（递归）

        也就是，对于树的每个节点，首先访问其左子树，然后再访问根节点，然后再访问其右子树。

为什么二叉搜索树的中序遍历是严格递增的

二叉搜索树（BST）的性质：
  • 左子树的所有节点值都小于根节点的值。
  • 右子树的所有节点值都大于根节点的值。
  • 对于每个节点，其左子树的所有节点值都比该节点小，其右子树的所有节点值都比该节点大。

这意味着：

  • 如果你从根节点出发，中序遍历时，会先遍历左子树，再访问当前节点，最后访问右子树。
  • 在访问当前节点时，它的值必须大于其左子树的最大值（因为左子树的节点值都小于当前节点），并且它的值必须小于其右子树的最小值（因为右子树的节点值都大于当前节点）。
中序遍历的结果：
  • 如果我们对一棵二叉搜索树进行中序遍历，遍历顺序是 左子树 -> 根节点 -> 右子树，这会确保遍历的顺序是递增的。
  • 具体来说：
    1. 左子树的节点值小于当前节点的值。
    2. 当前节点的值 小于右子树的节点值。
    所以，在中序遍历过程中，访问到的每个节点的值都会是比前一个节点值更大的，这也就是 严格递增。
举例：

假设有一棵简单的二叉搜索树，如下所示：

      4
     /  \
     2    6
     /  \  / \
     1   3 5   7

这棵树的中序遍历顺序如下：

  1. 先遍历左子树 (1, 2, 3)：
    • 访问节点 1 -> 访问节点 2 -> 访问节点 3
  2. 访问根节点 4
  3. 然后遍历右子树 (5, 6, 7)：
    • 访问节点 5 -> 访问节点 6 -> 访问节点 7

所以中序遍历得到的节点值是 1, 2, 3, 4, 5, 6, 7，这些值是 严格递增 的。

思路解析

  1. 二叉搜索树（BST）的性质：

    • 对于一个二叉搜索树，中序遍历 得到的节点值应该是 严格递增 的。
    • 也就是说，若中序遍历得到的节点值 v1, v2, v3, ..., vn 满足 v1 < v2 < v3 < ... < vn，那么该树是一个有效的二叉搜索树。

  2. 中序遍历的迭代实现：

    • 使用一个栈来模拟中序遍历的过程。
    • 栈用于保存当前节点的左子树路径，直到节点的左子树为空时，才会处理当前节点并遍历右子树。

  3. 检查 BST 的有效性：

    • 通过一个变量 inorder 来记录上一个访问的节点值（也就是上一个中序遍历的值）。
    • 如果当前节点的值小于或等于 inorder，则说明树不是一个有效的二叉搜索树，因为 BST 中序遍历的值必须是严格递增的。
    • 如果当前节点值大于 inorder，则更新 inorder 为当前节点的值，并继续遍历右子树。

  long inorder = -Long.MAX_VALUE;：用 inorder 变量来记录上一个节点的值，初始化为一个极小值。其实这第一种解法是我重新写的，因为每次的二叉树我都是先递归研究的所以，这里相同的问题我就不再赘述了，可以看下面解法二中的问题解决所提到的方法，为什么使用long。

Java写法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        // 使用栈来模拟中序遍历
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        
        // 用来记录上一个访问的节点的值，初始化为负无穷
        long checkValue = -Long.MAX_VALUE;

        // 遍历树，栈不为空或者当前节点不为null时继续处理
        while (!stack.isEmpty() || root != null) {
            // 先遍历左子树，压入栈中
            while (root != null) {
                stack.push(root);
                root = root.left;
            }

            // 弹出栈顶节点
            root = stack.pop();

            // 如果当前节点值小于等于上一个节点的值，说明不是二叉搜索树
            if (root.val <= checkValue) {
                return false;
            }

            // 更新当前节点的值
            checkValue = root.val;

            // 处理右子树
            root = root.right;
        }
        // 如果遍历完树没有发现问题，说明是有效的二叉搜索树
        return true;
    }
}

C++写法：

#include <stack>
#include <climits>  // 用于INT_MIN和INT_MAX

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        // 用栈模拟中序遍历
        stack<TreeNode*> stack;
        
        // 用一个变量记录上一个节点的值，初始化为负无穷
        long inorder = LONG_MIN;

        // 遍历树，栈不为空或者当前节点不为null时继续
        while (!stack.empty() || root != nullptr) {
            // 先遍历左子树，压入栈
            while (root != nullptr) {
                stack.push(root);
                root = root->left;
            }

            // 弹出栈顶节点
            root = stack.top();
            stack.pop();

            // 如果当前节点的值小于等于前一个节点的值，则不是二叉搜索树
            if (root->val <= inorder) {
                return false;
            }

            // 更新前一个节点的值
            inorder = root->val;

            // 处理右子树
            root = root->right;
        }

        // 如果整个遍历过程中没有发现问题，返回 true
        return true;
    }
};

运行时间

时间复杂度和空间复杂度

时间复杂度：

  • 时间复杂度：O(N)，其中 N 是树中的节点数。
    • 每个节点会被访问一次，栈的操作（压入和弹出）是常数时间 O(1)。
    • 所以整体的时间复杂度是树的节点数 N。

空间复杂度：

  • 空间复杂度：O(H)，其中 H 是树的高度。
    • 在最坏的情况下（例如树是链式结构），栈会存储所有的节点，栈的大小为 O(N)。
    • 在最好的情况下（树是平衡的），栈的最大大小为树的高度 O(log N)。
    • 因此，空间复杂度是 O(H)，其中 H 是树的高度。

解法二：递归遍历

  • 递归遍历： 通过递归的方式遍历二叉树的每一个节点，判断它是否符合二叉搜索树的要求。每个节点需要检查是否符合范围条件，这个范围是通过父节点传递下来的。

  • 递归函数 checkIsBSTree：

    • 输入参数： 每次递归调用时，node表示当前节点，smallValue表示当前节点值的下限，largeValue表示当前节点值的上限。对于每个节点，我们都需要检查它的值是否在smallValue和largeValue之间。
    • 返回值： 如果当前节点的值满足条件，并且它的左子树和右子树也满足条件，返回true；否则返回false。

  • 判断条件：

    • 空节点： 如果当前节点为空（即叶子节点的子节点），直接返回true，表示空节点符合任何二叉搜索树的要求。
    • 值的有效性： 如果当前节点的值不在smallValue和largeValue之间，则返回false，说明当前节点不符合BST的要求。

  • 递归左右子树：

    • 对于左子树，我们传递更新后的上限node.val（即当前节点值）作为右边界，因为左子树的值必须小于当前节点的值。
    • 对于右子树，我们传递更新后的下限node.val作为左边界，因为右子树的值必须大于当前节点的值。

  • 递归的终止条件：

    • 当递归到达叶子节点时，返回true，表示叶子节点本身符合BST的要求。
    • 如果发现某个节点值不在合法范围内，立即返回false，停止递归。

  • 上下界的合理性：

    • 由于我们在递归过程中会传递上下限，这样我们就可以确保每个节点都严格遵守其父节点的限制（左子树的节点值小于父节点，右子树的节点值大于父节点）。
    • 使用Long.MIN_VALUE和Long.MAX_VALUE作为初始范围，保证可以处理任何int范围内的数字。

假设我们有一棵二叉树：

       5
       /  \
       1   7
            / \
             6   8
 

  1. 首先调用checkIsBSTree(root, Long.MIN_VALUE, Long.MAX_VALUE)，即检查根节点5。
  2. 对于节点5，判断它是否在范围[Long.MIN_VALUE, Long.MAX_VALUE]内，显然是有效的。
  3. 然后递归检查它的左子树（节点1），checkIsBSTree(node.left, Long.MIN_VALUE, 5)，检查1是否在范围[Long.MIN_VALUE, 5]内，符合条件。
  4. 再递归检查右子树（节点7），checkIsBSTree(node.right, 5, Long.MAX_VALUE)，检查7是否在范围[5, Long.MAX_VALUE]内，符合条件。
  5. 继续递归检查节点7的左右子树，分别检查节点6和节点8，最终返回true，表示这棵树符合二叉搜索树的规则。

Java写法：

        这是我一开始的写法，就会有一个问题。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {

        return checkIsBSTree(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
    }

    /**
        用于判断是否在范围内
        左子树的值要在(smallValue, node.val)
        右子树的值要在(node.val, largeValue)
     */
    public boolean checkIsBSTree(TreeNode node, int smallValue, int largeValue){
        // 到了叶子节点还没发现不符合要求的则返回true
        if(node == null){
            return true;
        }

        // 判断节点值的合理性
        if(node.val <= smallValue || node.val >= largeValue){
            return false;
        }

        boolean left = checkIsBSTree(node.left, smallValue, node.val);
        boolean right = checkIsBSTree(node.right, node.val, largeValue);

        return left && right;

    }
}

        在执行到如下的示例的时候会毫不吝啬的错了。

        然后一开始我没反应过来，就直接做了个单节点判断，防止它继续报错。就在主方法加了如下的代码：

        if(root.left == null && root.right == null){
            return true;
        }

        就是校验了一下单节点，好了，刚才的用例就那么完美的过去了，然后我继续运行重新发现还有更加恐怖的事情发生了，这个用例又报错了。

        

        直到现在我才反应过来这个数字，这个数字就是在int类型下的最大的和最小的值，我们可以验证一下。

        验证代码

public class test {
    public static void main(String[] args) {
        System.out.println( "integer下的最大值" + Integer.MAX_VALUE);
        System.out.println( "integer下的最小值" + Integer.MIN_VALUE);
        System.out.println( "long下的最大值" + Long.MIN_VALUE);
        System.out.println( "long下的最小值" + Long.MIN_VALUE);
    }
}

        结果

integer下的最大值  2147483647    2^{31}
integer下的最小值 -2147483648    2^{31} - 1
long下的最大值   9223372036854775807  2^{63}
long下的最小值  -9223372036854775808  2^{63} - 1

 

        然后我就水灵灵了重新注意到了题目的取值范围如下。

        那么它就刚好可以取到2147483647这个值，而在我的判断false的逻辑中，写的是如下的代码。

        // 判断节点值的合理性
        if(node.val <= smallValue || node.val >= largeValue){
            return false;
        }

        这里就直接出事了，因为这里的node.val和largeValue是一样的，直接误判了，原因如下。

        Java中的Integer.MIN_VALUE是-2147483648，Integer.MAX_VALUE是2147483647，但是在判断树是否为二叉搜索树（BST）时，算法会将Integer.MAX_VALUE作为有效的右子树上界。因此，当node.val的值为2147483647时，node.val >= Integer.MAX_VALUE会成立，导致算法错误地认为这是一个无效的节点。

        呃这，那就直接采用long吧，其实这是一个好习惯对于算法比赛来说，因为真的很容易忽略这一点，但就是这一点就容易导致问题出现，我们追求的AC题目而不是让我们的代码在最快的执行速度下拥有最小的内存。

所以正确的Java写法如下

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return checkIsBSTree(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    /**
        用于判断是否在范围内
        左子树的值要在(smallValue, node.val)
        右子树的值要在(node.val, largeValue)
     */
    public boolean checkIsBSTree(TreeNode node, long smallValue, long largeValue){
        // 到了叶子节点还没发现不符合要求的则返回true
        if(node == null){
            return true;
        }

        // 判断节点值的合理性
        if(node.val <= smallValue || node.val >= largeValue){
            return false;
        }

        boolean left = checkIsBSTree(node.left, smallValue, node.val);
        boolean right = checkIsBSTree(node.right, node.val, largeValue);

        return left && right;

    }
}

C++写法：

#include <climits>  // 引入 LONG_MIN 和 LONG_MAX

// 定义二叉树节点结构
class TreeNode {
public:
    int val;        // 节点值
    TreeNode* left; // 左子树
    TreeNode* right; // 右子树
    
    // 构造函数
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int val) : val(val), left(nullptr), right(nullptr) {}
    TreeNode(int val, TreeNode* left, TreeNode* right) : val(val), left(left), right(right) {}
};

class Solution {
public:
    // 判断是否是有效的二叉搜索树
    bool isValidBST(TreeNode* root) {
        return checkIsBSTree(root, LONG_MIN, LONG_MAX);
    }

private:
    // 辅助递归函数，检查子树是否符合二叉搜索树的条件
    bool checkIsBSTree(TreeNode* node, long long smallValue, long long largeValue) {
        // 如果当前节点为空，返回 true，表示空树是有效的
        if (node == nullptr) {
            return true;
        }

        // 判断当前节点的值是否在有效的范围内
        if (node->val <= smallValue || node->val >= largeValue) {
            return false;  // 如果当前节点值不在范围内，返回 false
        }

        // 递归检查左子树，范围是 (smallValue, node->val)
        bool left = checkIsBSTree(node->left, smallValue, node->val);
        // 递归检查右子树，范围是 (node->val, largeValue)
        bool right = checkIsBSTree(node->right, node->val, largeValue);

        // 左右子树都符合条件时，返回 true，否则返回 false
        return left && right;
    }
};

运行时间

时间复杂度和空间复杂度

1. 时间复杂度（Time Complexity）

时间复杂度取决于二叉树的节点数目和我们访问每个节点的时间。

  • 对于每个节点，我们都要进行常数时间的操作：检查节点值是否在合法范围内、递归检查左子树和右子树。
  • 由于我们是递归遍历整棵二叉树，且每个节点都只被访问一次，因此时间复杂度为 O(N)，其中 N 是二叉树中的节点数目。

2. 空间复杂度分析（Space Complexity）

        在递归算法中，空间复杂度的关键因素是 递归栈 的深度，因为每一次递归调用都会将一个栈帧压入栈中。我们需要根据二叉树的结构来评估最大可能的递归栈深度。

1. 递归栈空间：
  • 每次递归调用都会为当前节点分配一个栈帧。
  • 因此，空间复杂度不仅取决于输入数据，还取决于递归的深度，即二叉树的高度。
2. 二叉树的高度：
  • 最坏情况下，二叉树呈现 链状结构，即每个节点只有一个子节点（左或右），树的高度为 n（树的节点数）。这种情况下，递归栈深度也为 n，所以空间复杂度为 O(n)。
  • 最好情况下，二叉树是 完全平衡 的，树的高度为 log(n)，这时递归栈深度为 log(n)，空间复杂度为 O(log n)。
3. 所以：
  • 在递归过程中，由于每一层的递归调用会占用栈空间，空间复杂度取决于递归的深度。
  • 最坏情况下：当二叉树呈链状时，递归的深度为 n，因此空间复杂度为 O(n)。
  • 最好情况下：当二叉树是完全平衡的时，递归的深度为 log n，因此空间复杂度为 O(log n)。

总结

二叉搜索树的特点是：

  • 对于每个节点，左子树的所有节点值小于该节点，右子树的所有节点值大于该节点。
  • 中序遍历结果应该是严格递增的。

解决方案：

  1. 递归方式：通过递归地检查每个节点是否满足左子树小于该节点，右子树大于该节点，利用递归函数传递上下界来判断。

    • 时间复杂度：O(N)，遍历每个节点一次。
    • 空间复杂度：O(H)，H 是树的高度，最坏情况下递归栈的深度为树的高度。

  2. 迭代方式：使用栈模拟中序遍历，同时检查每次访问的节点值是否符合严格递增的要求。

    • 时间复杂度：O(N)，每个节点访问一次。
    • 空间复杂度：O(H)，栈的最大深度为树的高度，最坏情况下为 O(N)。

关键点：

  • 通过中序遍历检查树的节点是否严格递增。
  • 迭代方式通过显式栈模拟递归，避免了递归栈溢出的风险，但在极端不平衡树上可能需要更多空间。


http://www.kler.cn/a/381040.html

相关文章：

  • LeetCode：1387. 将整数按权重排序（记忆化搜索 Java）
  • c# 后台任务自动执行
  • Vue 92 ，Element 15 ，Vue + el-upload 实现图片上传与管理
  • typora数学符号
  • ARM异常处理 M33
  • UE5 猎户座漂浮小岛 12 技能 瞬移 重力控制
  • 计算机存储单元bit。不同编程语言类型差异。
  • Python面向对象：类和对象的基本操作
  • 在gitlab，把新分支替换成master分支
  • LeetCode 3165.不包含相邻元素的子序列的最大和：单点修改的线段树（动态规划）
  • easyui +vue v-slot 注意事项
  • Grafana+Prometheus监控篇-Nginx
  • C#中，Thread和Task的区别
  • 人工智能基础-opencv-图像处理篇
  • 第二届新生程序设计竞赛热身赛(C语言）
  • File和InputStream，OutputStream
  • JavaEE初阶---网络原理值TCP篇（三）
  • gradle下载的jar包，源码出现Decompiled .class file, bytecode version
  • nginx监控指标有哪些
  • AI开发-三方库-torch-torchvision
  • Redis学习：BigKey、缓存双写一致性更新策略和案例
  • 小土堆学习笔记15：搭建小实战和Sequential的使用
  • w~自动驾驶~合集4
  • 【深度学习】DreamClear：提升图片分辨率的模型
  • git cherry-pick 小技巧
  • 【日志】初学顺序表