【学习笔记】计算机视觉与深度学习(4.卷积神经网络)
学习视频:
鲁鹏-计算机视觉与深度学习
同系列往期笔记:
【学习笔记】计算机视觉与深度学习(1.线性分类器)
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)
【学习笔记】计算机视觉与深度学习(3.卷积与图像去噪/边缘提取/纹理表示)
1 全连接神经网络的弊端
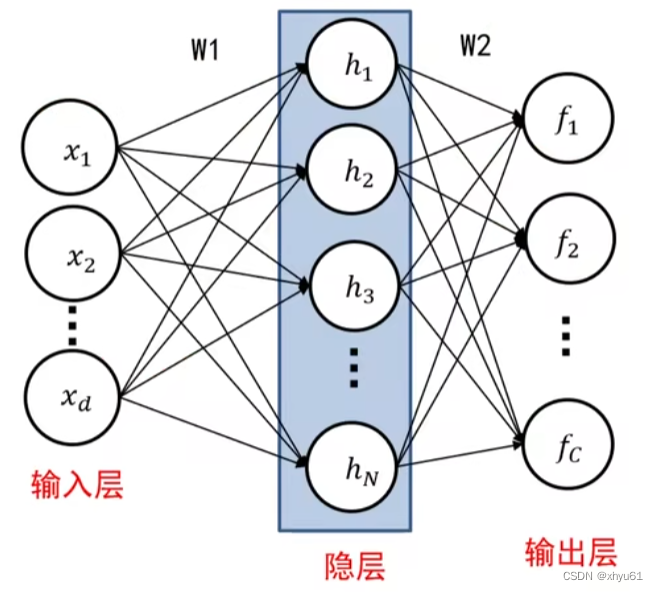
上图是两层全连接网络。
问 CIFAR10图像尺寸为
32
×
32
×
3
=
3072
32\times 32\times 3=3072
32×32×3=3072,那么隐藏层每个神经元权值个数是多少?
答 共
3072
+
1
=
3073
3072+1=3073
3072+1=3073个,加的一个是偏置参数
b
b
b。
问 如果图像尺寸为
200
×
200
×
3
=
120000
200\times 200\times 3=120000
200×200×3=120000,那么隐藏层每个神经元权值个数是多少?
答 共
120000
+
1
=
120001
120000+1=120001
120000+1=120001个。
可以看出,这样的结构参数太多,很容易过拟合。
不难看出,当图像越大时,全连接神经网络的结构越大,计算量难以接受。其实这和图像的表示方法有关系,全连接神经网络更适合向量维数较少的表示方法。
通过上一个笔记中所学的卷积中的方法,我们可以先对图像进行特征的提取,假设提取出 48 48 48个特征,然后我们将这 48 48 48维的向量作为全连接神经网络的输入,或许是一种可行的办法?
2 卷积神经网络
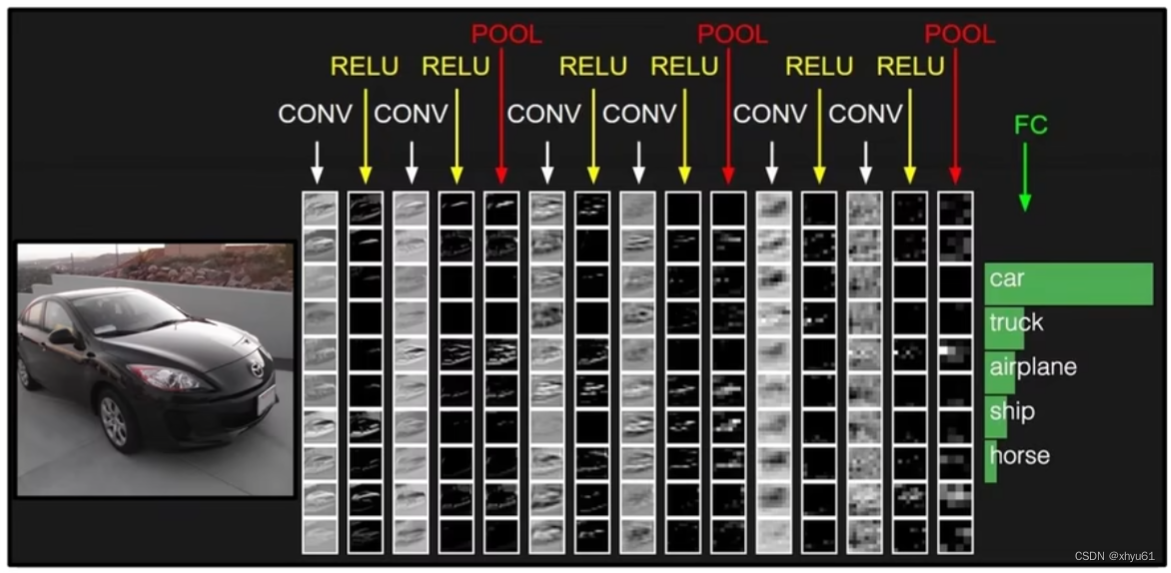
其中
CONV:卷积层
RELU:激活层
POOL:池化层
FC:全连接层
2.1 卷积层
2.1.1 回顾:基于卷积核组的图像表示
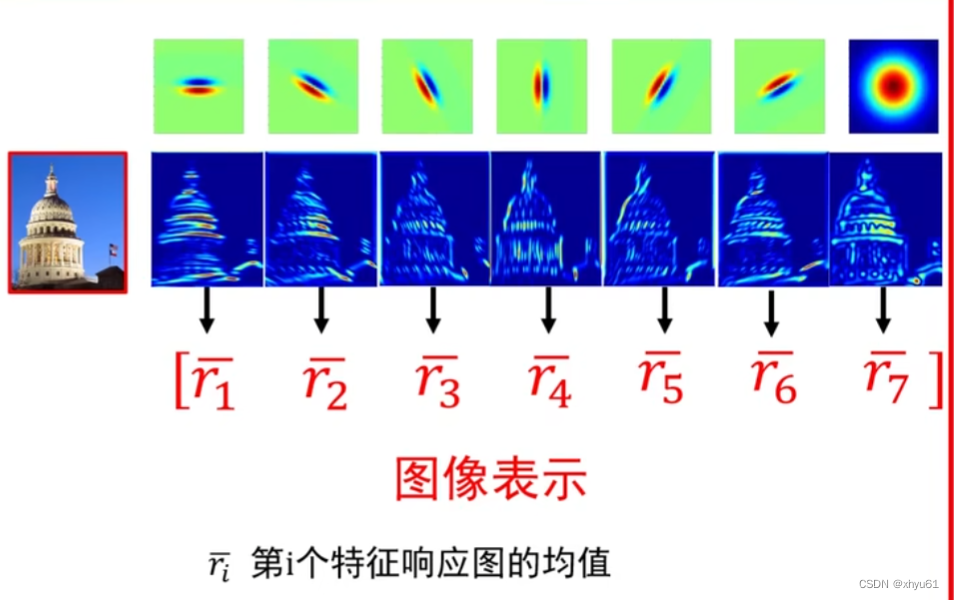
2.1.2 卷积神经网络中的卷积核
- 不仅具有宽和高,还具有深度,常写成:宽度 × \times ×高度 × \times ×深度
- 卷积核参数不仅包括核中存储的权值,还包括一个偏置值。
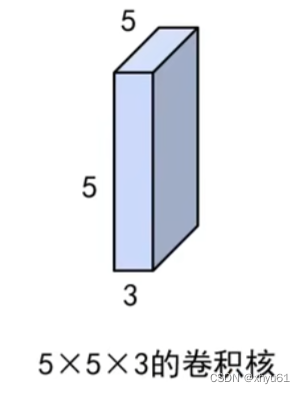
2.1.3 卷积神经网络中的卷积操作
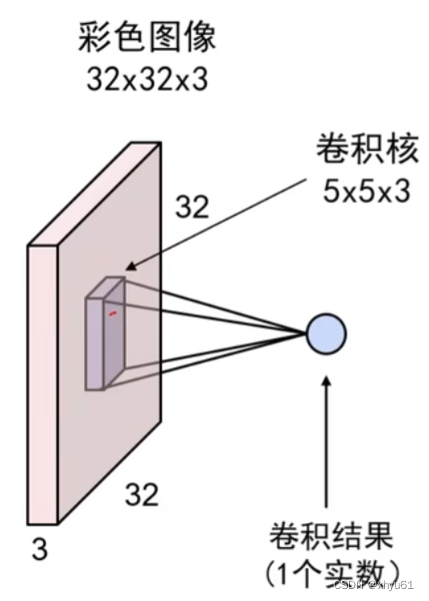
计算过程:
将卷积核展成一个 5 × 5 × 3 5\times 5\times 3 5×5×3的向量,同时将其覆盖的图像区域按相同的展开方式展成 5 × 5 × 3 5\times5\times3 5×5×3的向量;
计算两者的点乘;
在点乘的结果上加偏移量。
数学公式:
w
T
x
+
b
\mathbf{w}^T\mathbf{x}+b
wTx+b
其中
w
\mathbf{w}
w为卷积核的权值矩阵,
b
b
b为卷积核的偏置。
2.1.4 卷积层
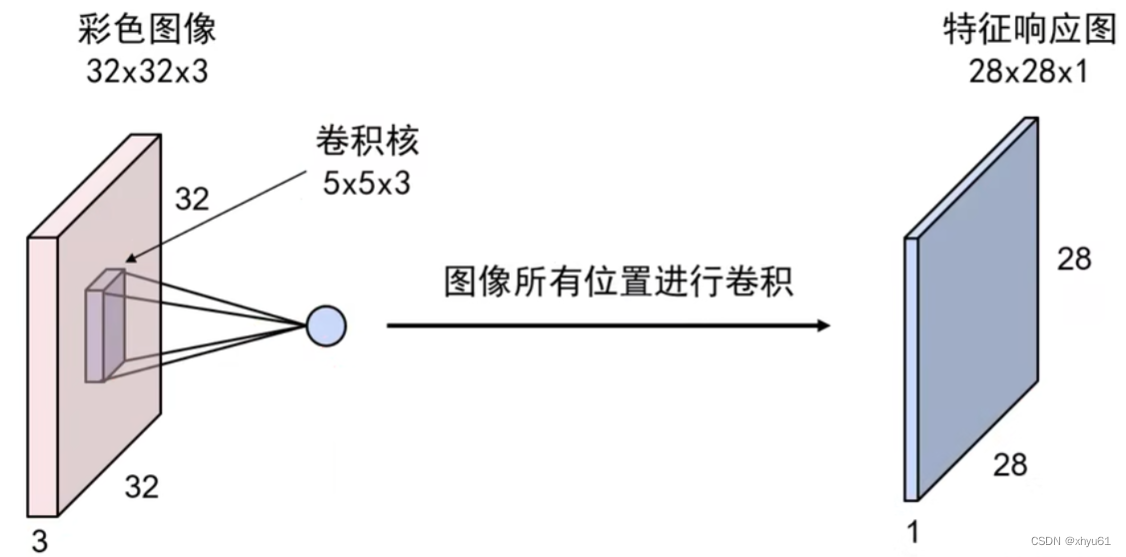
特征响应图中每一个位置上的值反映了图像上对应位置是否存在卷积核所记录的基元结构信息。
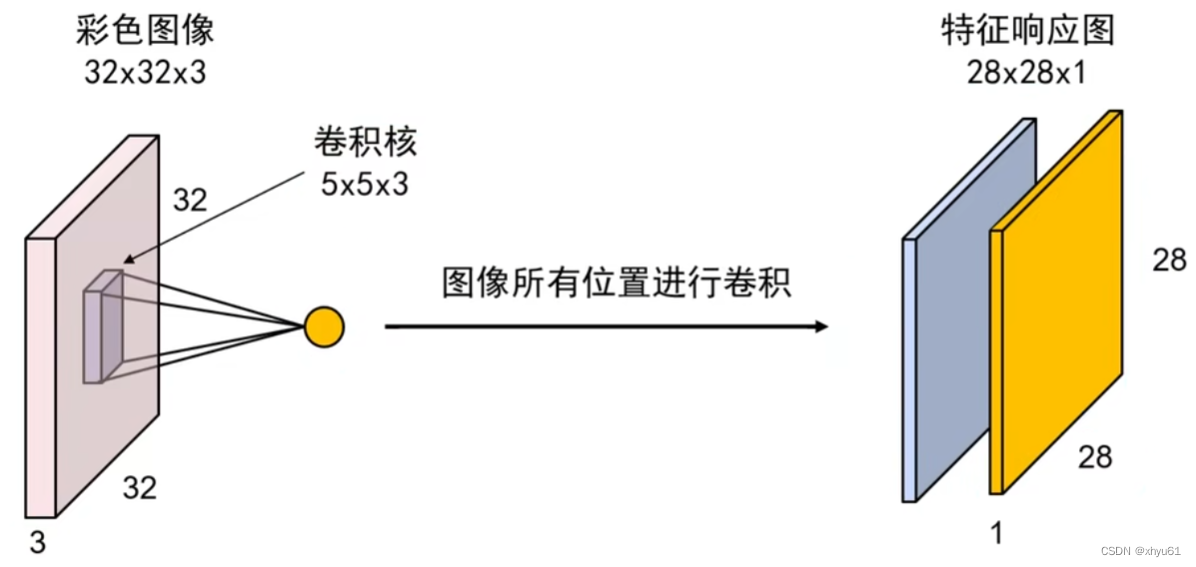
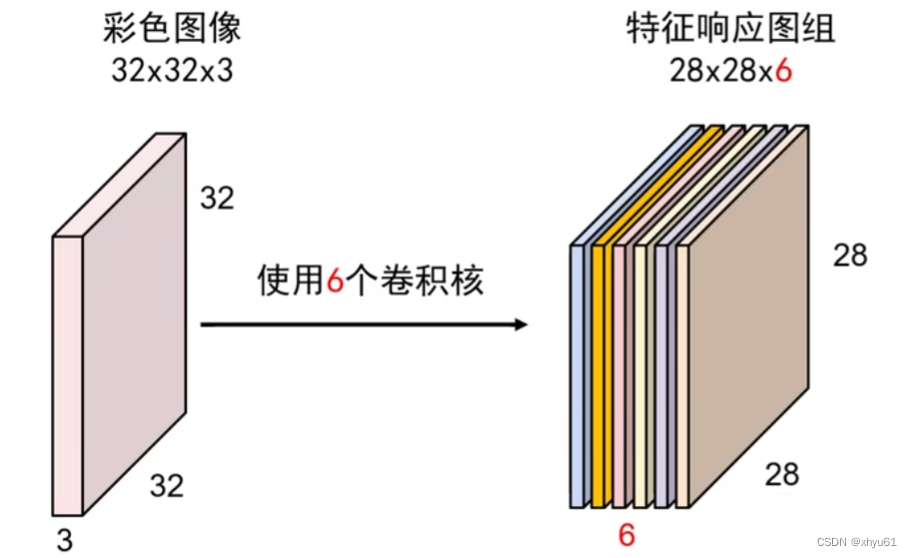
可以看出:
- 特征相应图组深度等于卷积核的个数;
- 不同的特征响应图反映了输入图像对不同卷积核的影响结果;
- 同一特征响应图上不同位置的值表示输入图像上不同位置对同一卷积核的响应结果。
2.1.5 卷积步长
卷积神经网络中,卷积核可以按照指定的间隔进行卷积操作,这个间隔就是卷积步长。
不难想到,卷积步长越大,卷积后得到的卷积结果越小。
输入数据矩阵尺寸
W
1
×
H
1
W_1\times H_1
W1×H1、输出特征图组尺寸
W
2
×
H
2
W_2\times H_2
W2×H2、卷积核尺寸
F
F
F、卷积步长
S
S
S,则
W
2
,
H
2
W_2,H_2
W2,H2与
W
1
,
H
1
W_1,H_1
W1,H1的关系如下:
W
2
=
(
W
1
−
F
)
/
S
+
1
W_2=(W_1-F)/S+1
W2=(W1−F)/S+1
H
2
=
(
H
1
−
F
)
/
S
+
1
H_2=(H_1-F)/S+1
H2=(H1−F)/S+1
2.1.6 边界填充
卷积神经网络中最常用的填充方式是零值填充。边界填充可以保证卷积的输入输出尺寸相同。
输入数据矩阵尺寸
W
1
×
H
1
W_1\times H_1
W1×H1、输出特征图组尺寸
W
2
×
H
2
W_2\times H_2
W2×H2、卷积核尺寸
F
F
F、卷积步长
S
S
S、
P
P
P为零填充层数,则
W
2
,
H
2
W_2,H_2
W2,H2与
W
1
,
H
1
W_1,H_1
W1,H1的关系如下:
W
2
=
(
W
1
−
F
+
2
P
)
/
S
+
1
W_2=(W_1-F+2P)/S+1
W2=(W1−F+2P)/S+1
H
2
=
(
H
1
−
F
+
2
P
)
/
S
+
1
H_2=(H_1-F+2P)/S+1
H2=(H1−F+2P)/S+1
设计网络时,我们可以通过该公式将
P
P
P求出。
2.1.7 特征相应图组尺寸计算
给定输入数据矩阵时,影响输出的特征图组尺寸大小的因素:
- 卷积核的宽、高
- 是否采用边界填充操作
- 卷积步长
- 该层的卷积核个数
设输入数据矩阵尺寸为
W
1
×
H
1
×
D
1
W_1\times H_1\times D_1
W1×H1×D1、输出特征图组尺寸为
W
2
×
H
2
×
D
2
W_2\times H_2\times D_2
W2×H2×D2、卷积核尺寸
F
F
F、卷积步长
S
S
S、零填充层数
P
P
P、卷积核个数
K
K
K。其中
F
,
S
,
P
,
K
F,S,P,K
F,S,P,K为卷积核的4个超参数。卷积核深度和
D
1
D_1
D1自适应。那么特征图组尺寸计算如下:
W
2
=
(
W
1
−
F
+
2
P
)
/
S
+
1
W_2=(W_1-F+2P)/S+1
W2=(W1−F+2P)/S+1
H
2
=
(
H
1
−
F
+
2
P
)
/
S
+
1
H_2=(H_1-F+2P)/S+1
H2=(H1−F+2P)/S+1
D
2
=
K
D_2=K
D2=K(卷积核个数=特征图深度,是前面提到的结论)
2.2 激活层
和全连接神经网络中的激活函数是一模一样的作用,将得到的三维数据中的每一个元素通过激活函数转化一下即可。
2.3 池化层
2.3.1 池化操作
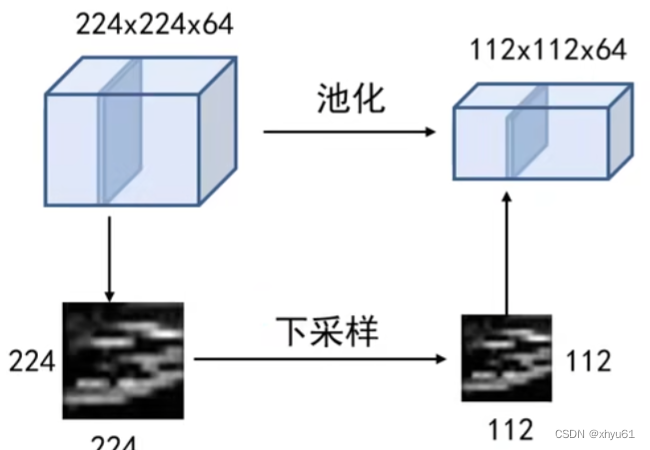
池化的作用:对每一个特征响应图独立进行,降低特征响应图组中每个特征响应图的宽度和高度,减少后续卷积层的参数数量,降低计算资源耗费,进而控制过拟合。
更具体地说,卷积操作后的结果通常会交给下一层去使用,而如果我们想要提取的特征数较多,导致特征图的深度变大,那么交给下一层的数据就会膨胀。当我们的图片像素很大时,这增加了后续的运算量和所需的存储空间。因此我们需要减小响应图的宽度和高度来降低数据量,以达到降低计算资源耗费的目标。
同时,对于同样尺寸的卷积核,当我们的卷积目标更小时,卷积核所探测到的特征将会是更加趋于整张图片的总体特征情况,这对控制过拟合也是有好处的。
池化操作:对特征响应图某个区域进行池化就是在该区域上指定一个值来代表整个区域。
常见池化操作:
最大池化——使用区域内的最大值来代表这个区域;
平均池化——采用区域内的所有值的均值作为代表。
池化层的超参数:池化窗口和池化步长
2.3.2 池化操作举例
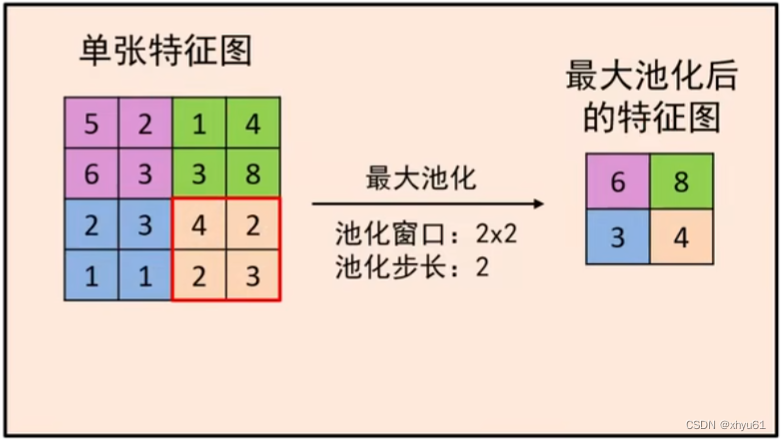
(最大池化和前面介绍的非最大化抑制的思想很相像)
操作后,特征响应图中的75%的响应信息都丢掉,但不改变特征响应图的个数。
2.4 全连接层
和全连接神经网络相同,卷积神经网络的侧重点在于优化全连接神经网络的输入中图像表示。经过卷积神经网络后,我们得到了原图像基于多个卷积核的表现结果,即特征图。我们有两种方法形成全连接神经网络的输入:
- 将卷积核对应的特征图转化成向量,拼到一起形成全连接神经网络的输入向量
- 将卷积核对应的特征图信息取均值,拼到一起形成全连接神经网络的输入向量
3 图像增强
存在的问题:过拟合的原因是学习样本过少,导致无法训练出能够泛化到新数据的类型。
数据增强:是从现有的训练样本中生成更多的训练数据,其方法是利用多种能够生成可信图像的随机变换来增加样本。
数据增强的目标:模型在训练时不会两次查看完全相同的图像,这让模型能够观察到数据的更多内容,从而具有更好的泛化能力。
3.1 样本增强的方法
3.1.1 翻转
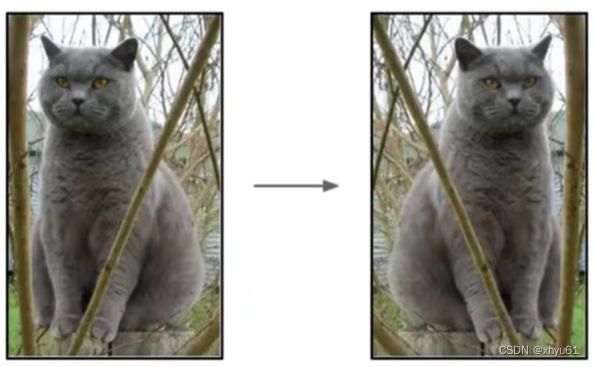
既学了朝左的猫,也学了朝右的猫。
3.1.2 随机缩放&抠图

以残差网络中的样本增强方法为例。
输入要求:
224
×
224
224\times 224
224×224的彩色图片
训练阶段:在不同尺度、不同区域随机抠取
- 在[256,480]之间随机选择一个尺寸 L L L
- 将训练样本缩放至短边 = L =L =L
- 在该样本上随机采样一个 224 × 224 224\times 224 224×224的图像区域
测试阶段:按照一套预先定义的方式抠取
- 将图像缩放至5种尺寸:{224, 256, 384, 480, 640}
- 对每一个尺度的图像及其镜像图像,分别在其四个角及中间位置抠取 224 × 224 224\times 224 224×224区域,即可获得10个图像。
3.1.3 色彩抖动
换个颜色也不是不行喵。
色彩抖动操作步骤:
- 利用主成分分析方法提取当前图像的色彩数据([R G B])的主轴
- 沿着主轴方向随机采样一个偏移
- 将偏移量加入当前图像的每个像素
3.1.4 更多操作
平移、旋转、拉伸、径向畸变、裁剪……
