1. 小和问题

什么是小和问题呢？

这是一个数组，我们要求每一个数左边比当前数小的数的和累加起来。
2的左边没有数，说明它的小和为0。
4的左边2比4小，说明它的小和为1个2。
2的左边没有数比它小，说明它的小和为0。
1的左边没有数比它小，说明它的小和为0。
3的左边2和1比它小，说明它的小和为2个2和1个1为5。
6的左边所有数都比它小，说明它的小和为2+4+2+1+3=12。
3的左边2和1比它小，说明它的小和为2个2和1个1为5。
4的左边1，2，3比4小，说明它的小和为1个1，2个2，2个3为11。
1的左边没有数比它小，说明它的小和为0。
5的左边除了6都比5小，说明它的小和为20。
然后再把所有小和加起来：0+2+0+0+5+12+5+11+0+20=55。

那么怎么在归并排序中解决这个问题呢？

首先，下标0和下标1归并，2小于4，拷贝左边的，然后拷贝右边的。如果拷贝左边的则产生小和，那么右边有1个比2大，产生的小和个数是下标1-0=1，也就是1个2。

因为一个数不需要继续，然后下标[0，1]和[2，2]归并。首先，2和2相等，相等的时候，一定要先拷贝右边的。因为你不知道右边有多少个比当前的值大。

现在下标3和下标4归并，1小于3，先拷贝左边的，拷贝左边的就会产生小和，右边有4-3=1个比3大的。所以产生的小和数是1个1。

现在是下标[0，2]和[3，4]归并，2大于1，先拷贝右边的，拷贝右边的不产生小和。

2小于3，拷贝左边的，产生小和，产生1个2。往后移一位，还是2小于3，拷贝左边的，产生小和，产生1个2。往后移一位。

此时3小于4，拷贝右边的，不产生小和，最后再拷贝左边的，也不产生小和。后面的原理都是类似的。

总结：
1.拷贝左边的产生小和，拷贝右边的不产生小和。
2.相等的时候，一定要先拷贝右边的，因为不知道右边的有多少个数比它大。

这样做的原理是什么？
原来是算左边有多少个比它小的，现在我们算某一个数右边有多少个比它大的，如果比它大的，就会产生几个它(此时它就作为小和)。

代码实现：

2. 逆序对

什么叫做逆序对呢？
左边的数比右的数大的就叫做逆序对。

举个例子：

这个数组中，有多少个逆序对呢？(3，1)，(3，0)，(3，1)，(1，0)，(4，3)，(4，1)，(3，1)。总共有这么7个逆序对。

解题思路：
上面的小和问题求的是右边比它大，而这道题其实求的是右边比它小的。

这里还是利用归并排序的原理，其余的不变，但是在归并的时候需要一些变化。

当我们开始归并的时候，我们需要从后往前开始遍历。相等的时候，还是先拷贝右边的，因为我们不知道右边会有多少个比我小。

此时，右边的比左边小，我们就能算出当前6的逆序对，用下标直接相减就能得出。然后把左边的拷贝下来。

此时3小于4，就把右边的4拷贝下来，然后还是4，再把右边的4拷贝下来。

此时3大于2，我们就可以算出3的逆序对。这就是求逆序对的一个流程，我们需要在归并排序中进行一些改变。

代码如下：

这里要注意，一定要控制好下标，不然就会出错。

3. num>x*2的问题

这道题求的是：某个数num右边有多少个数乘2都小于等于num。

举个例子：

那么在这个数组中满足条件的有：(6，1)，(6，2)，(7，1)，(7，3)，(7，2)。就这么几个满足条件。

思路流程：

这是在合并之前的操作。此时1<1 * 2，所以右边的下标不能动，我们移动左边的下标。

此时4大于1 * 2，右边的下标需要一直移动。

当移动到下标为2的时候，移动不了了。此时我们就可以使用下标相减的方式来算出有多少个比它小的。然后左边的继续移动。

现在右边的可以移动了。就按照这样的流程。当左边的数组结束，循环就结束了。

我们是在合并前，去完成这个事情。完成这个事情的时间复杂度是O(N)，后面合并的过程也是O(N)，没有什么太多的影响。

4. 区间和的个数

难度 困难 题目链接

这道题的意思是：给定一个数组，和两个整数lower和upper，返回数组中有多少个子数组的累加和在[lower，upper]上。

解题思路：
首先，我们在解这道题前，我们需要了解一个前缀和的知识，如果大家不懂前缀和，可以看一下这篇文章：前缀和讲解！

第一步：我们要求所有下标的子数组，看有多少个子数组满足要求。
下标为0的子数组：[0，0]
下标为1的子数组：[0，1]，[1，1]
下标为2的子数组：[0，2]，[1，2]，[2，2]
… …
我们把满足要求的个数加起来返回就可以。

第二步：把前缀和数组先搞出来。

这里我们用的是long long，因为防止int类型溢出。

第三步：转换符合范围的策略。
假设某个子数组[i，j]的累加和(也就是前缀和sum(i，j))在[lower，upper]上，说明sum(0，j) - sum(0，i-1)也在[lower，upper]上。那么我们可以进行转换：sum(0，i-1)在sum(0，j) - [lower，upper]范围上，就说明sum(i，j)在[lower，upper]上。

举个例子：
假设[lower，upper]为[10，40]，sum(0，17)为100，我们要求以17结尾的所有子数组有多少个在[10，40]上。[x，17]是由sum(0，17) - sum(0，x-1)得到的，如果我们想让[x，17]在[10，40]范围上，那么sum(0，x-1)的范围要在[60，90]，这样[x，17]才能在[10，40]范围上。

总结：假设0到 i 整体的累加和是x，求以i为结尾的子数组有多少个在[lower，upper]上，等同于去求 i 之前的所有前缀和中，有多少个前缀和在[x-upper，x-lower]上。

所以，在前缀和数组中，我们想求以x为结尾的子数组有多少在[lower，upper]上的，就可以转换成在x前面有多少个前缀和在[x-upper，x-lower]上。想求以y为结尾的子数组有多少在[lower，upper]上的，就可以转换成在y前面有多少个前缀和在[y-upper，y-lower]上。依此类推。

第四步：合并之前找出有多少个符合要求。
举个例子：

假设这两个要开始合并，范围是[-1，2]，我们是从右边的数组里开始去找左边有多少个前缀和在[x-upper，x-lower]上。

比如6这个数，那么我们就要看左边有多少个数在[4，7]这个范围上。7这个数，就要看左边有多少个在[5，8]这个范围上。8这个数就要看有多少个在[6，9]上。从这里，你可以发现：[4，7]，[5，8]，[6，9]，下限和上限都是不断增加的，也就是说它不会回退。这样这个操作的时间复杂度是O(N)。

然后，我们可以定义一个left和right：

6的范围是：[4，7]，先走right，我们可以看到R走到8的时候就超过上限了，就不能走了。然后走left，我们可以看到L走到5的时候就不需要走了，因为大于下限了。

此时，只有一个数5在[4，7]这个范围上，我们直接R-L就能得出个数。后面的过程也是一样的道理。

代码实现：

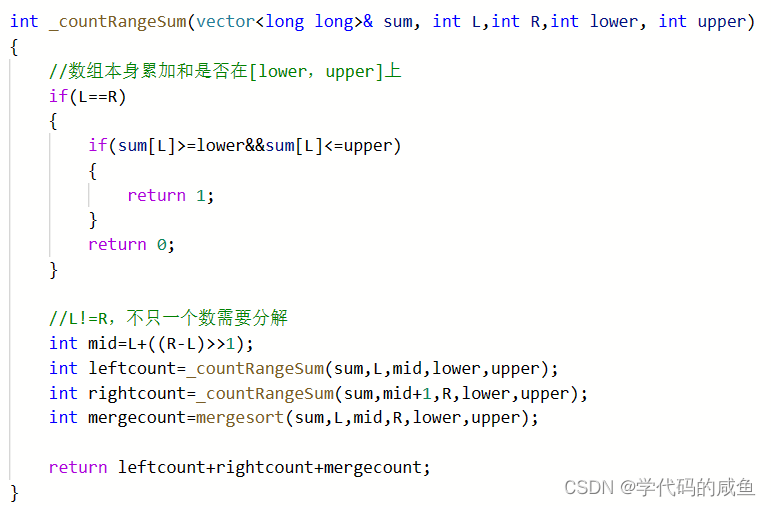
首先，我们需要划分到一个数，然后看这个数本身是否在范围上。因为我们传的是sum，所以它是[0，L]的累加和。然后总的个数是左边的个数+右边的个数+合并之前的个数。

完整代码：

class Solution {
public:
    
    int _countRangeSum(vector<long long>& sum, int L,int R,int lower, int upper)
    {
        //数组本身累加和是否在[lower，upper]上
        if(L==R)
        {
            if(sum[L]>=lower&&sum[L]<=upper)
            {
                return 1;
            }
            return 0;
        }

        //L!=R，不只一个数需要分解
        int mid=L+((R-L)>>1);
        int leftcount=_countRangeSum(sum,L,mid,lower,upper);
        int rightcount=_countRangeSum(sum,mid+1,R,lower,upper);
        int mergecount=mergesort(sum,L,mid,R,lower,upper);

        return leftcount+rightcount+mergecount;
    }

    int mergesort(vector<long long>& sum,int L,int mid,int R,int lower,int upper)
    {
        //合并之前，对于右边数组中每个数x，求左边数组中有多少个数位于[x-upper，x-lower]
        int ret=0;
        int begin1=L,end1=L;
        int begin2=mid+1,end2=R;

        while(begin2<=end2)
        {
            long long min=sum[begin2]-upper;
            long long max=sum[begin2]-lower;
            while(end1<=mid&&sum[end1]<=max)
            {
                end1++;
            }

            while(begin1<=mid&&sum[begin1]<min)
            {
                begin1++;
            }
            ret+=end1-begin1;

            begin2++;
        }

        long long* tmp=new long long[R-L+1];
        int left=L;
        int right=mid+1;
        int index=0;
        while(left<=mid&&right<=R)
        {
            if(sum[left]<sum[right])
            {
                tmp[index++]=sum[left++];
            }
            else
            {
                tmp[index++]=sum[right++];
            }
        }

        while(left<=mid)
        {
            tmp[index++]=sum[left++];
        }

        while(right<=R)
        {
            tmp[index++]=sum[right++];
        }

        for (int i = 0; i <R-L+1; ++i) {
            sum[L + i] = tmp[i];
        }

        return ret;
    }



    int countRangeSum(vector<int>& nums, int lower, int upper) {
        //前缀和数组
        vector<long long> sum;
        sum.resize(nums.size());
        sum[0]=nums[0];
        for(int i=1;i<nums.size();i++)
        {
            sum[i]=sum[i-1]+nums[i];
        }

        return _countRangeSum(sum,0,sum.size()-1,lower,upper);

    }
};