数据结构:二叉树
目录
1.完全二叉树和链式二叉树
2.普通二叉树的增删查改没有意义
3.前中后序遍历
4.递归的时间复杂度看的是深度
5.二叉树的分治
6.递归函数中传入的参数
1.完全二叉树和链式二叉树
完全二叉树可以用数组表示。
链式二叉树只能用链式结构表示
2.普通二叉树的增删查改没有意义
普通二叉树存储数据没有意义,不如链表和数组
加个性质就有意义了,搜索二叉树,左子树比根小,右子树比根大。类似于二分查找(只不过二分查找必须有序)每搜索一次,减少一半的搜索对象。
二分查找的缺点:1.要求有序
2.要求在数组里
3.不适合增删查改
数据结构搜索:搜索二叉树->平衡二叉搜索树,哈希表,B树
3.前中后序遍历
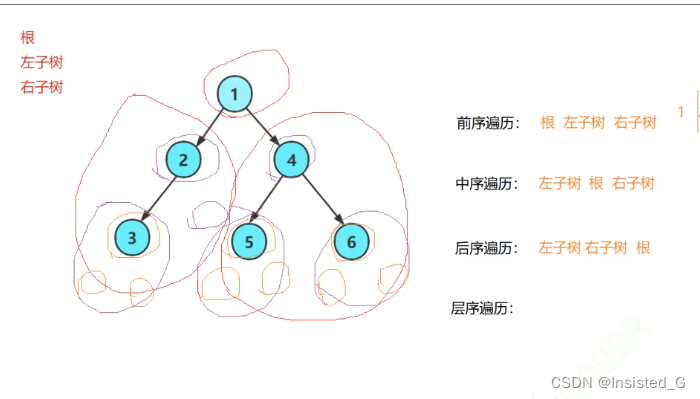
看待树的方式:根,左子树,右子树
前序遍历:根 左子树 右子树
中序遍历:null 3 null 2 null 1 null 5 null 4 null 6 null
后序遍历(左 右 根):null null 3 null 2 null null 5 null null 6 4 1
前中后遍历递归什么时候回来?
为空的时候返回,其余都要一直递归下去(递归注意结束条件)
层序遍历:1 2 4 3 5 6
4.递归的时间复杂度看的是深度
递归的时间复杂度看的是深度,而不是递归的次数
因为递归中会还给操作系统栈帧。
栈帧会保存传入的参数
5.二叉树的分治
分治求二叉树的大小
求树的高度
不关心具体的实现,只需写出来方法,具体的需要递归实现
6.递归函数中传入的参数
递归会创建许多的栈帧,每个如果这些栈帧中传入的参数是简单的int i,那么在不同中栈帧中对这个i 修改不会影响到其他的栈帧。所以说递归传入参数的时候最好传入指针,这样在每个栈帧对这个指针的内容修改都会影响到其他栈帧
144. 二叉树的前序遍历 - 力扣(LeetCode)
这道题就是经典的递归传入参数要传指针的问题