当前位置： 首页 > article >正文

蓝桥杯训练day5

article 2024/12/28 1:11:00

kmp，单调栈，单调队列，trie树

  • 1.kmp算法
    • （1）831. KMP字符串
  • 2.单调栈
    • （1）830. 单调栈
  • 3.单调队列
    • （1）154. 滑动窗口
    • （2）135. 最大子序和
    • （3）1089. 烽火传递
    • （4）299. 裁剪序列
  • 4.trie树（字典树）
    • （1）835. Trie字符串统计
    • (2)143. 最大异或对
    • (3)3485. 最大异或和

1.kmp算法

（1）831. KMP字符串

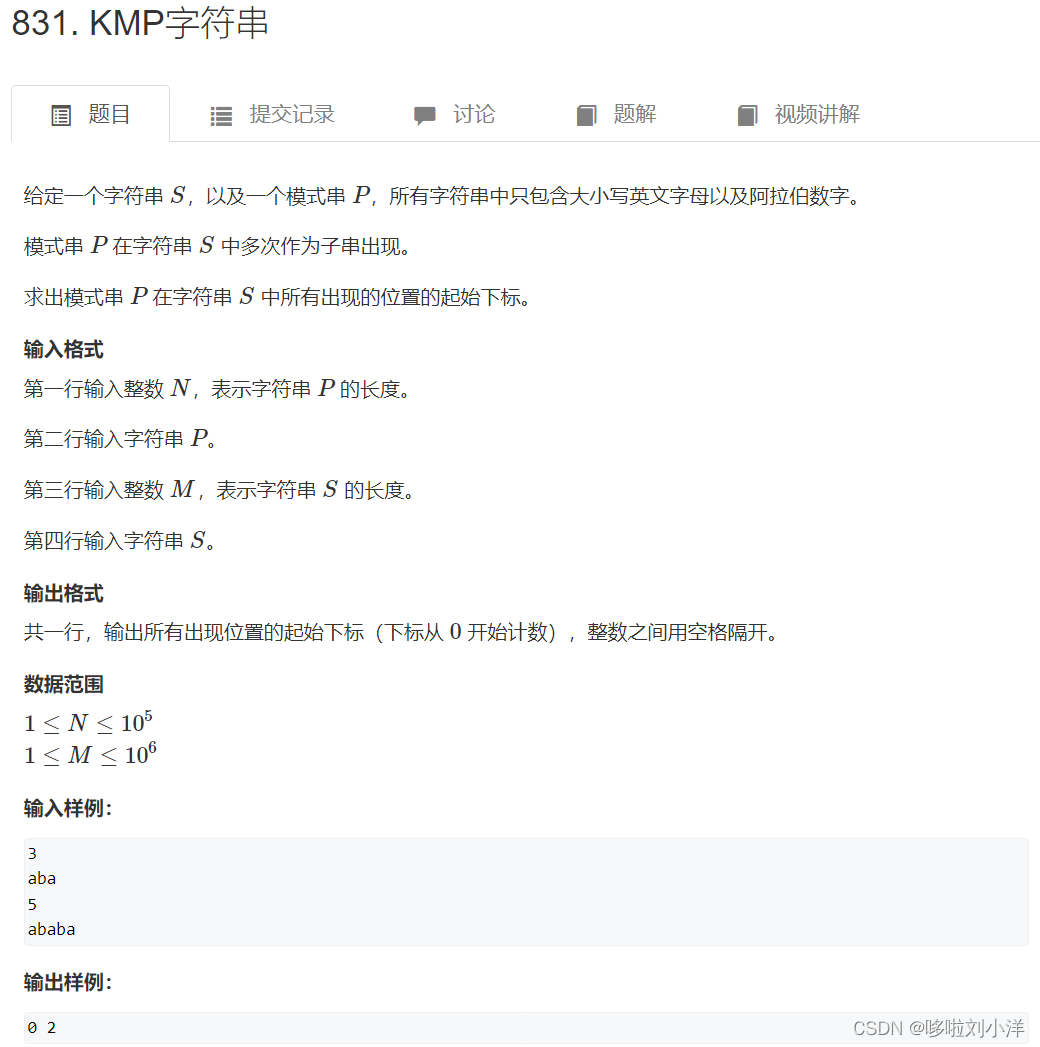
在这里插入图片描述

p是模式串，s是主串

第一步：算出p的最长前后缀，用两个p来求
第二部：算出p在s中的位置，用p和s来求

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e6+10;

char s[N],p[N];

int ne[N];


int n,m;


int main()
{
    cin>>n;
    scanf("%s",p+1);
    cin>>m;
    scanf("%s",s+1);
    
    for(int i=2,j=0;i<=n;i++)
    {
        while(j&&p[i]!=p[j+1])j=ne[j];
        if(p[i]==p[j+1])j++;
        ne[i]=j;
    }
    
    for(int i=1,j=0;i<=m;i++)
    {
        while(j&&s[i]!=p[j+1])j=ne[j];
        if(s[i]==p[j+1])j++;
        if(j==n)
        {
            cout<<i-n<<" ";
            j=ne[j];
        }
    }
    
    return 0;
}

2.单调栈

（1）830. 单调栈

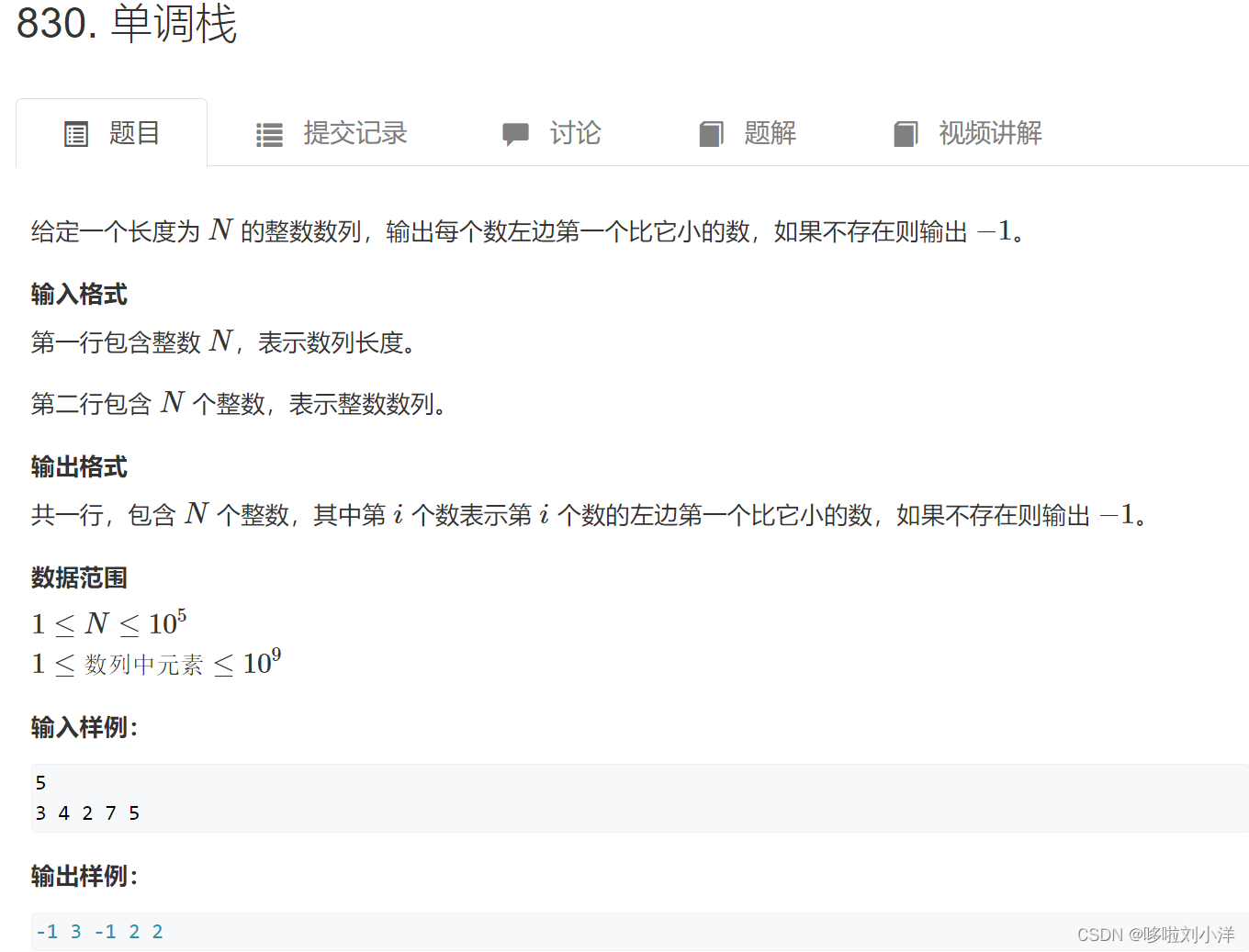
在这里插入图片描述

单调栈模板题
思路：
整理了一下：
求左边第一个小的数，等价于求右边第一个小的数（将答案倒过来即可），从左往右使用单调递增的栈
求左边第一个大的数，等价于求右边第一个大的数（将答案倒过来即可），从左往右使用单调递减的栈

#include<iostream>
#include<stack>
using namespace std;

const int N=1e5+10;
int a[N];
int ans[N];

stack<int>st;

int n;

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
        
    for(int i=0;i<n;i++)  //保证栈单调递增
    {
        while(!st.empty()&&a[st.top()]>=a[i])st.pop();
        if(st.empty())ans[i]=-1;  //表示第i个元素左边没有比他小的数
        else ans[i]=a[st.top()];
        st.push(i);
    }
    
    for(int i=0;i<n;i++)
        cout<<ans[i]<<" ";
    return 0;
    
}

3.单调队列

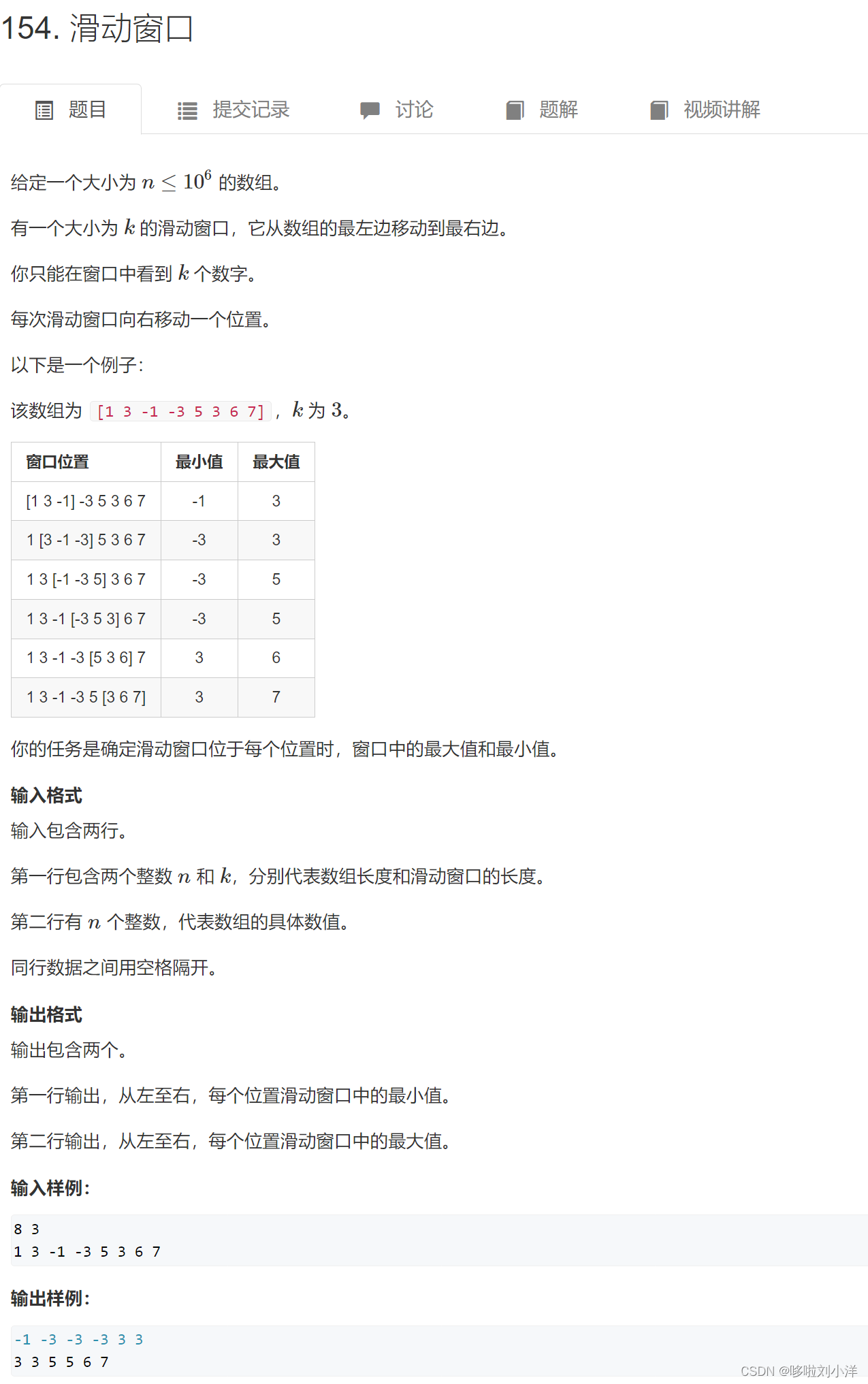
（1）154. 滑动窗口

在这里插入图片描述

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;


const int N=1e6+10;

int a[N];
deque<int>q;


int n,k;


int main()
{
    cin>>n>>k;
    for(int i=0;i<n;i++)
        cin>>a[i];
    
    for(int i=0;i<n;i++)  //保证递增(从队头到队尾)
    {
        if(!q.empty()&&q.front()<i-k+1)q.pop_front();
        while(!q.empty()&&a[q.back()]>=a[i])q.pop_back();
        q.push_back(i);
        if(i-k+1>=0)
            cout<<a[q.front()]<<" ";
    }
    cout<<endl;
    q.clear();
    for(int i=0;i<n;i++)  //保证递减
    {
        if(!q.empty()&&q.front()<i-k+1)q.pop_front();
        while(!q.empty()&&a[q.back()]<=a[i])q.pop_back();
        q.push_back(i);
        if(i-k+1>=0)
            cout<<a[q.front()]<<" ";
    }
    return 0;
}

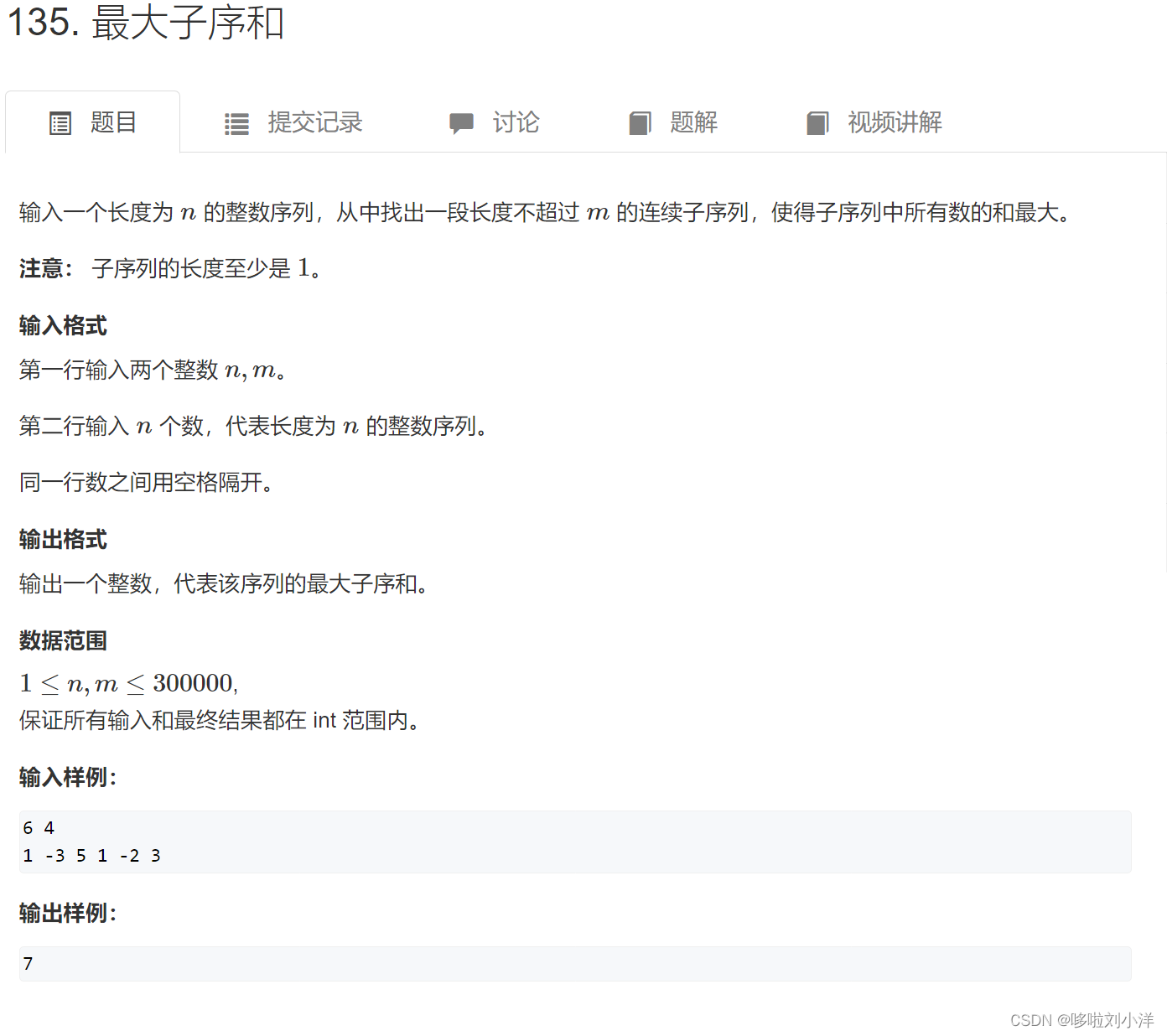
（2）135. 最大子序和

在这里插入图片描述

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;


const int N=3*1e6+10;

int n,m;

int a[N];
int s[N];

deque<int>q;

int ans;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
        
    for(int i=1;i<=n;i++)
        s[i]=s[i-1]+a[i];
    
    ans=-0x3f3f3f3f;
    q.push_back(0);
    for(int i=1;i<=n;i++)
    {
        if(!q.empty()&&q.front()<i-m)  //为什么是i-m，模拟一下
            q.pop_front();
        if(!q.empty())
            ans=max(ans,s[i]-s[q.front()]);
        while(!q.empty()&&s[q.back()]>=s[i])q.pop_back();
        q.push_back(i);
    }
    cout<<ans;
    return 0;
}

（3）1089. 烽火传递

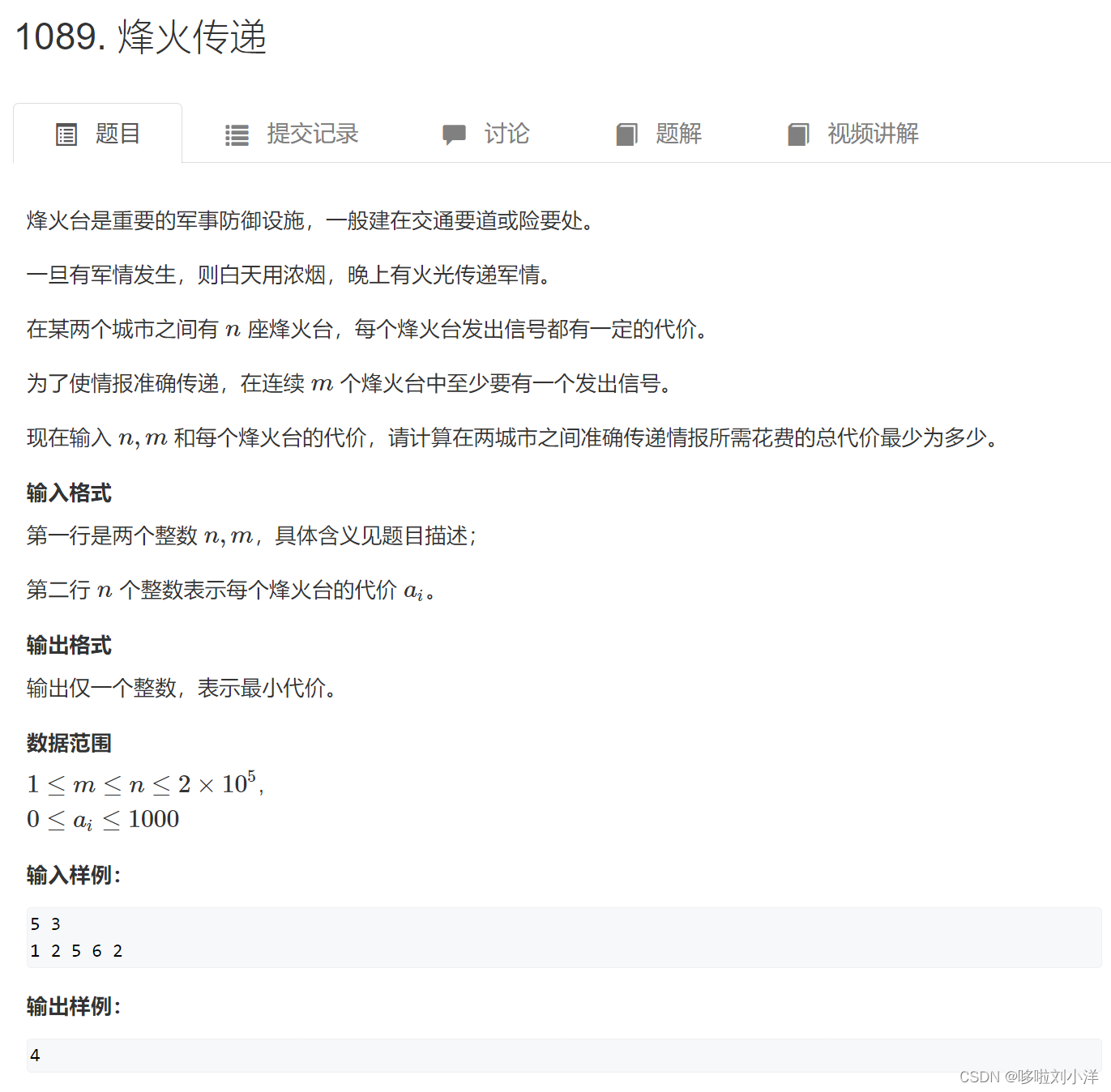
在这里插入图片描述

首先，可以敏锐的发现这是一道动态规划的题目，如果没有察觉，说明题目做少了。

定义：
f [ i ] 表示前 1 到 i − 1 座烽火塔点燃的最小价值 + 第 i 座烽火一定点燃的价值 f[i]表示前1到i-1座烽火塔点燃的最小价值+第i座烽火一定点燃的价值 f[i]表示前1到i−1座烽火塔点燃的最小价值+第i座烽火一定点燃的价值
f [ i ] = m i n ( f [ i − 1 ] , f [ i − 2 ] , f [ i − 3 ] . . . f [ i − m ] ) + v a l u e [ i ] f[i]=min(f[i-1],f[i-2],f[i-3]...f[i-m])+value[i] f[i]=min(f[i−1],f[i−2],f[i−3]...f[i−m])+value[i]

很明显，每次计算一次f[i]，都要找到前面m个f的最小值，这可以想到单调队列维护最值。
那么尝试写一下代码。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=2*1e5+10;

int value[N];
int q[N];
int dp[N];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>value[i];
        
    int tt=0,hh=0;   //tt是队尾，hh是队头
    dp[0]=0;
    
    for(int i=1;i<=n;i++)  //维护单调队列的递增性，每次都取队头(队列的容量是m)
    {
        if(hh<=tt&&q[hh]<i-m)hh++;  //维护单调队列的队头的范围，不能与i超过m个间隔
        dp[i]=dp[q[hh]]+value[i];
        while(hh<=tt&&dp[i]<dp[q[tt]])tt--;
        q[++tt]=i;
    }
    
    int res=0x3f3f3f3f;
    for(int i=n-m+1;i<=n;i++)  //答案在最后一段找
        res=min(res,dp[i]);
    cout<<res<<endl;
    return  0;
    
}

（4）299. 裁剪序列

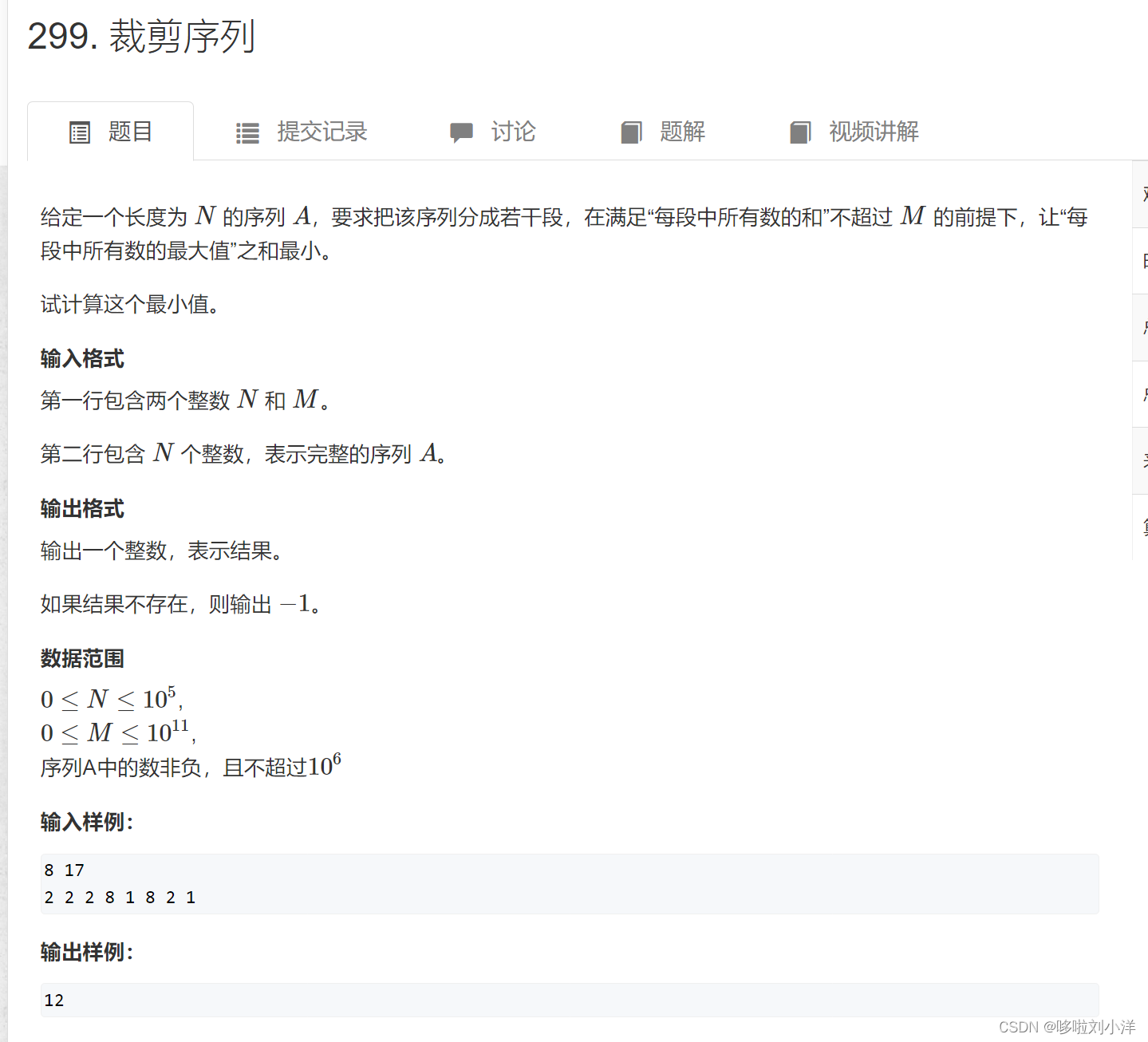
在这里插入图片描述
国赛难度，暂时不写。

在这里插入代码片

4.trie树（字典树）

（1）835. Trie字符串统计

在这里插入图片描述

son[p][u]表示单前单词的下一个单词所在层数.idx++的目的是防止单词重复记录

#include<iostream>
#include<cstring>

using namespace std;

const int N=100010;

int son[N][26];
int idx;
int cnt[N];


int n;

void Insert(string &str)
{
    int p=0;
    for(int i=0;i<str.size();i++)
    {
        int u=str[i]-'a';
        if(son[p][u]==0)son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]+=1;
    
}

int find(string &str)
{
    int p=0;
    for(int i=0;i<str.size();i++)
    {
        int u=str[i]-'a';
        if(son[p][u]==0)return 0;
        p=son[p][u];
    }
    return cnt[p];
}

int main()
{
    cin>>n;
    while(n--)
    {
        char op;
        cin>>op;
        string str;
        cin>>str;
        if(op=='I')
        {
            Insert(str);
        }
        else
        {
            cout<<find(str);
            cout<<endl;
        }
       
        
    }
    return 0;
}

(2)143. 最大异或对

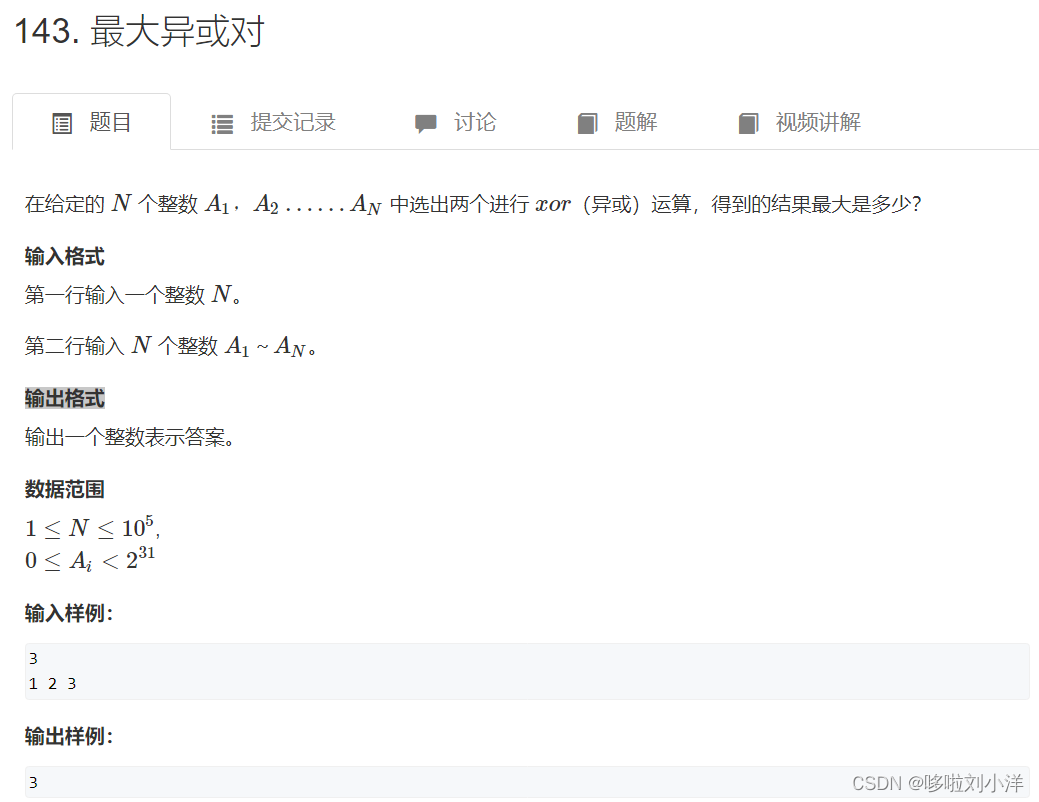
在这里插入图片描述
首先异或运算的规则是：相同则0，相反则1

#include<iostream>
#include<cstring>
using namespace std;

const int N=1e5+10,M=31*N;

int a[N];
int son[M][2];
int idx;

int n;


void Insert(int x)   //将一个数拆分成二进制，相当于只有两种字符的字符串
{
    int p=0;
    for(int i=30;i>=0;i--)
    {
        int u=x>>i&1;  //表示x的从右往左第i+1位二进制是多少
        if(son[p][u]==0)son[p][u]=++idx;
        p=son[p][u];
    }
    
}

int find(int x)
{
    int p=0;
    int ans=0;
    for(int i=30;i>=0;i--)  //根据异或的规则，相同的为0，相反的为1,从高位到低位，尽量找到1
    {
        int u=x>>i&1;
        if(son[p][!u]==0)//没有1，只能找0了
            p=son[p][u];
        else
        {
            ans+=1<<i;
            p=son[p][!u];
        }
    }
    return ans;
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
        
    int ans=0;
    for(int i=0;i<n;i++)
        Insert(a[i]);
        
    for(int i=0;i<n;i++)
        ans=max(ans,find(a[i]));
    
    cout<<ans;
    
    return 0;
    
        
}

(3)3485. 最大异或和

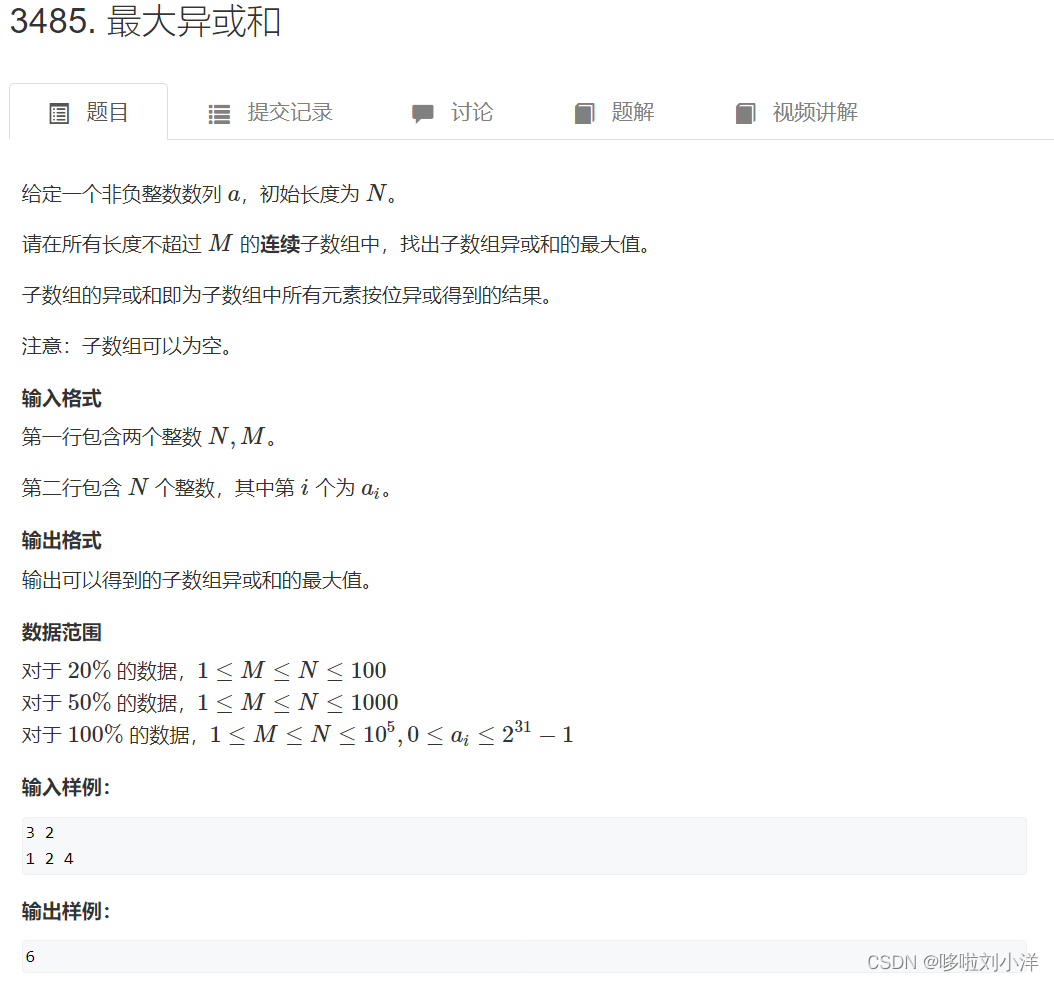
在这里插入图片描述

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=31*1e5+10;
int son[N][2];
int cnt[N];
int idx;
int sum[N];



int n,m;

void insert(int x,int k)
{
    int p=0;
    for(int i=30;i>=0;i--)
    {
        int u=x>>i&1;
        if(son[p][u]==0)son[p][u]=++idx;
        p=son[p][u];
        cnt[p]+=k;   //每个节点出现的次数
    }
    
}

int find(int x)
{
    int p=0;
    int ans=0;
    for(int i=30;i>=0;i--)
    {
        int u=x>>i&1;
        if(cnt[son[p][!u]])
        {
            ans+=1<<i;
            p=son[p][!u];
        }
        else
        {
            p=son[p][u];
        }
            
    }
    return ans;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int x;
        cin>>x;
        sum[i]=sum[i-1]^x;
    }
    
    insert(sum[0],1);  //将0插入
    
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(i-m-1>=0)insert(sum[i-m-1],-1);  //删除窗口之外的数，一个数异或一个值两次会变成原样
        ans=max(ans,find(sum[i]));
        insert(sum[i],1);
    }
    cout<<ans;
    return 0;
}

http://www.kler.cn/a/6305.html

相关文章：

  • ArkTs组件（2）
  • 【安全编码】Web平台如何设计防止重放攻击
  • 【UE5 C++课程系列笔记】13——GameInstanceSubsystem的简单使用
  • 浅谈ORACLE中间件SOA BPM,IDM,OID,UCM,WebcenterPortal服务器如何做迁移切换
  • 深入理解 PyTorch 的 view() 函数：以多头注意力机制（Multi-Head Attention）为例 （中英双语）
  • 排序算法之快速排序、归并排序
  • 【深度学习】基于Hough变化的答题卡识别（Matlab代码实现）
  • Text to image论文精读GigaGAN: 生成对抗网络仍然是文本生成图像的可行选择
  • day30 ● 332.重新安排行程 ● 51. N皇后 ● 37. 解数独
  • OBProxy 路由策略与使用运维-使用和运维
  • c++全排列 next_permutation（）函数
  • 字节测试总监，让我们用这份《测试用例规范》，再也没加班过
  • 【故障诊断】基于最小熵反卷积、最大相关峰度反卷积和最大二阶环平稳盲反卷积等盲反卷积方法在机械故障诊断中的应用研究（Matlab代码实现）
  • vue尚品汇商城项目-day03【20.获取Banner轮播图的数据+21.使用swiper轮播图插件】
  • 【ZGC】为什么初始标记需要STW(stop the world) ？
  • 操作系统-AOSOA
  • AnaXNet: Anatomy Aware Multi-label Finding Classification in Chest X-ray
  • java14 使用增强的模式匹配切换表达式
  • Android 热修复小结
  • 从零开始实现一个C++高性能服务器框架----IO协程调度模块
  • word打latex公式显示不成功，出现【 打不出左大括号
  • Springboot高级（一）缓存
  • （七）Tomcat源码阅读：Host组件分析
  • 熬夜肝完~ 阿里P8的Java进阶知识典藏版，我从18K飙到30K
  • 【js】超详细js函数基础
  • React createContext 与 useContext 的基本使用