40. 组合总和 II
题目链接:力扣
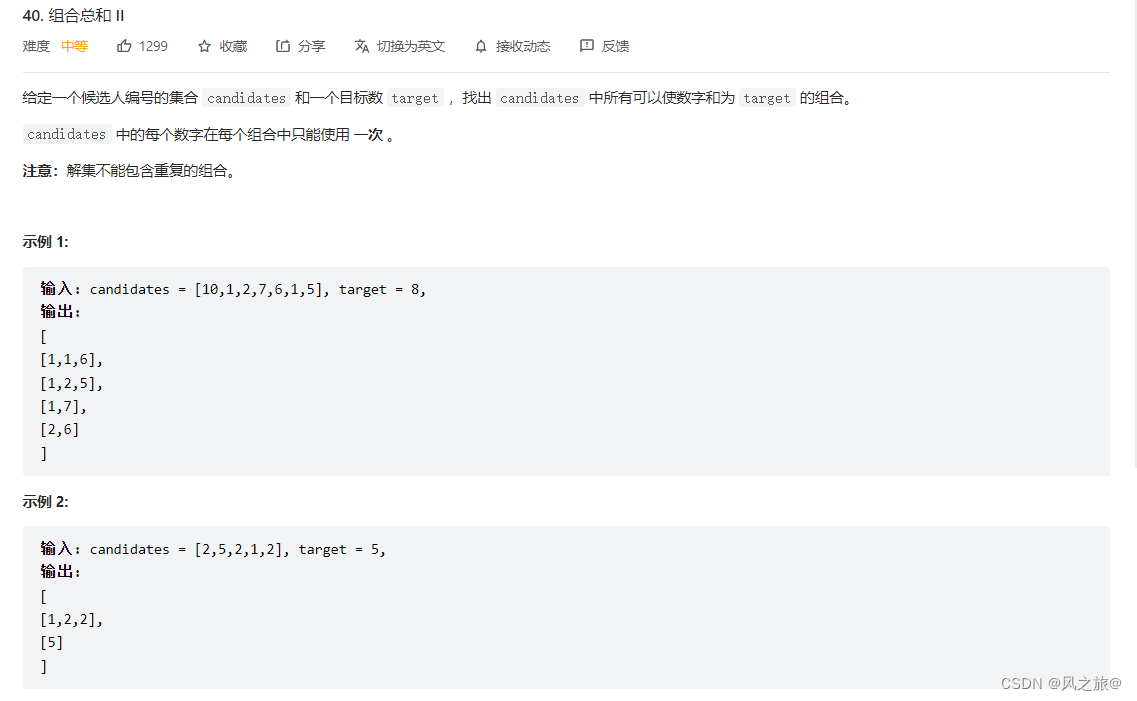
解题思路:类似于力扣39题,组合总和,这里不同的是每个数字在每个组合中只能使用一次,但是数字可能会重复,所以,可以先统计candidates中每个数字出现的次数保存在candidatesNum数组中,然后使用一个新数组newCandidates保存candidates不重复的元素。
那么新的题意可以转化为:给你一个 无重复元素的整数数组newCandidates和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的所有不同组合,candidates 中的同一个数字最多只能选取candidatesNum中保存的次数。如果至少一个数字的被选数量不同,则两种组合是不同的。
这样就可以完全使用第39题的解法解决这道题,
第39题解法参考博客地址:39. 组合总和_风之旅@的博客-CSDN博客
解题思路:递归+回溯
- 定义递归函数:isCombinationSun2(int[] candidates, int[] candidatesNum, int target, List<Integer> tem, List<List<Integer>> result, int index):表示在当前待选择的数为candidates[index],与已经选择过的数字进行组合,candidatesNum表示每个数字最多可以选择的次数,target表示还剩多少需要进行组合,tem表示已经选择的组合,result保存所有有效的答案,:
- 递归终止条件:
- 如果target==0,则已经成功组合成target,此时tem中保存的既是一个答案,将tem加入到result中
- 如果index==candidates.length,说明所有的candidates中的元素已经使用完了,直接return
- 令k = Math.min(candidatesNum[candidates[index]], target/candidates[index]),k表示最多可以选用candidates[index]多少次。
- 本次递归可以不选用candidates[index]进行组合,进入递归isCombinationSun2(candidates, candidatesNum,target, tem, result, index + 1);
- 本次递归选用candidates[index]进行组合,最多只能选用k次,for循环k次:
- tem.add(candidates[index])
- target -= candidates[index];
- isCombinationSun2(candidates, candidatesNum,target, tem, result, index + 1)。进入下一层递归,在下一层递归中又会对candidates[index+1]进行选择0次或者多次组合,注意,这里当进入下一次for循环时,即从这里的递归返回时,需要将在isCombinationSun(candidates, target, tem, result, index + 1)递归后面所有新加入的候选数字从tem中删除,因为,本轮中重新选择的候选数字,显然后续递归中的所有候选都已经失效了,也就是回溯的意义!
- 回溯
- 依次将本轮递归中新加入到tem中的candidates[index]删除,回退到上一轮递归
- 删除本轮递归中新加入的candidates[index],在回退到上一轮递归时,上一轮中会重新选择新的候选数字加入到tem中,所以本轮递归中选择的候选数字就变成无效的了,需要从tem中删除,当本轮选择的候选数字是有效组合中的其中一个,那么在回溯删除之前,已经把有效的tem加入到result中了,删除本轮递归中新加入的candidates[index],并不会影响已经找到的答案
- 递归终止条件:
- AC代码
class Solution {
public static List<List<Integer>> combinationSum2(int[] candidates, int target) {
int[] candidatesNum = new int[51];
int count = 0;
for (int i = 0; i < candidates.length; i++) {
if (candidatesNum[candidates[i]] == 0) {
count++;
}
candidatesNum[candidates[i]]++;
}
int[] newCandidates = new int[count];
count = 0;
for (int i = 0; i < candidatesNum.length; i++) {
if (candidatesNum[i] > 0) {
newCandidates[count++] = i;
}
}
List<List<Integer>> result = new LinkedList<>();
List<Integer> tem = new ArrayList<>();
isCombinationSun2(newCandidates,candidatesNum, target, tem, result, 0);
return result;
}
public static void isCombinationSun2(int[] candidates, int[] candidatesNum, int target, List<Integer> tem, List<List<Integer>> result, int index) {
if (target == 0) {
result.add(new LinkedList<>(tem));
return;
}
if (index == candidates.length) {
return;
}
int len = tem.size();
//不选当前
isCombinationSun2(candidates, candidatesNum,target, tem, result, index + 1);
int k = Math.min(candidatesNum[candidates[index]],target/candidates[index]);
for (int i = 0; i <k;i++){
tem.add(candidates[index]);
target -= candidates[index];
isCombinationSun2(candidates, candidatesNum,target, tem, result, index + 1);
}
int newLen = tem.size();
for (int i = 0; i < newLen - len; i++) {
tem.remove(newLen - i - 1);
}
}
}