2022蓝桥杯省赛——砍竹子
问题描述
这天, 小明在砍竹子, 他面前有 n 棵竹子排成一排,一开始第 i 棵竹子的 高度为 hi。
他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 H, 那么用一次魔法可以把这一段竹子的高度都变为![]() ,其中⌊x⌋ 表示对 x 向下取整。小明想知道他最少使用多少次魔法可让所有的竹子的高度都变为 1 。
,其中⌊x⌋ 表示对 x 向下取整。小明想知道他最少使用多少次魔法可让所有的竹子的高度都变为 1 。
输入格式
第一行为一个正整数 n,表示竹子的棵数。
第二行共 n 个空格分开的正整数 hi, 表示每棵竹子的高度。
输出格式
一个整数表示答案。
样例输入
6
2 1 4 2 6 7
样例输出
5
样例说明
其中一种方案:
214267

共需要 5 步完成。
评测用例规模与约定
对于 20% 的数据,保证 n≤1000,hi≤10^6 。对于 100% 的数据,保证 n≤2×10^5,hi≤10^18。
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 2s | 256M |
| C | 2s | 256M |
| Java | 5s | 256M |
| Python3 | 10s | 256M |
问题分析
把每棵竹子砍到1,每砍一次计数器加1;再回来看第i和第i-1棵竹子在砍的时候是否有出现相同的高度,每出现一次计数器减1。
我们需要建立一个二维数组,每一行存储一棵竹子从原始高度到1的高度变化。二维数组的行数我们已知是n,我们还需要知道它的列数。从评测用例规模中我们可以看到,竹子的最大高度为10^18,通过循环我们易求出二维数组的列数最大值是m=6。
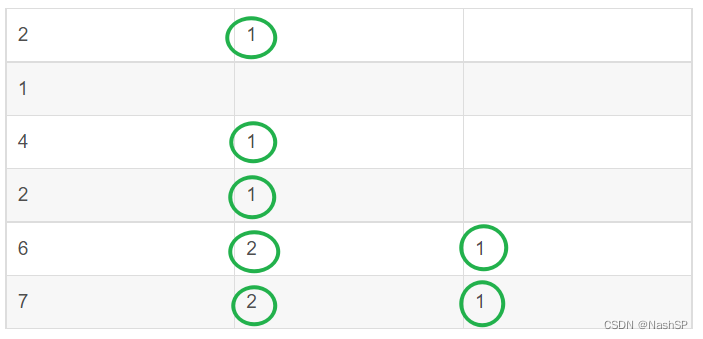
在构建二维数组的同时,进行计数器加操作,易得此时count=7。但是,通过这个二维数组我们无法进行计数器减操作。因此,为了方便计算,我们将该二维数组左右翻转,格式仍保持左对齐,得到如下形式:
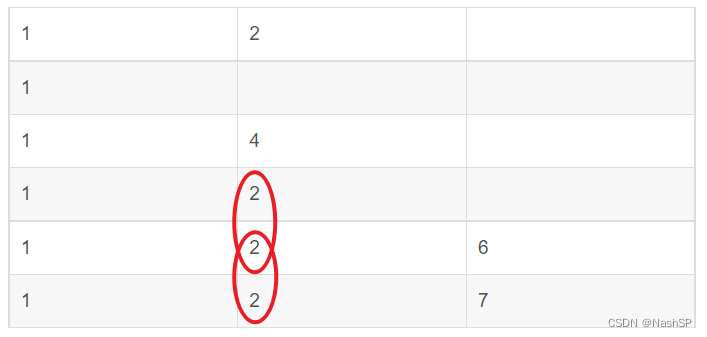
这样一来,我们就能很直观地看出来,有两次砍竹子的动作是多余的,于是执行两次计数器减操作。
Python代码如下:
import math
H=10**18 # 最大高度
n=int(input()) # 竹子的棵数
a=list(map(int,input().split()))
# 砍竹子
def cut(h):
return int(math.sqrt(int(h/2)+1))
# 假设最多需要砍m次,求m
m=-1
for i in range(10):
H=cut(H)
if H==1:
m=i+1 # i是从0开始计的,而m最小是1,故加一
break
# print(m)
h=[[] for i in range(n)]
count=0 # 所求次数
# 构造二维数组
for i in range(n):
hh=a[i]
h[i].insert(0,hh)
while hh>1:
hh=cut(hh)
h[i].insert(0,hh) # 每次都插到行首,这样就能实现二维数组的左右翻转
count+=1
# 逐列扫描二维数组
for j in range(1,m+1): # 列标
for i in range(1,n): # 行标
if j<len(h[i]):
if j<len(h[i-1]) and h[i][j]==h[i-1][j]: # 当前的竹子和前一棵竹子高度一致
count-=1
else:
continue
print(count)但是我这个代码的通过率只有65%,目前还不知道哪里需要改进,欢迎读者批评指正。

