当前位置：首页 > article >正文

吴恩达机器学习--逻辑回归

article 2024/11/18 3:41:17

文章目录

前言
一、普通二分类逻辑回归
- 需求分析
- 程序设计
- - 1. 导入数据
  - 2. 可视化数据
  - 3. 划分数据
  - 4. sigmoid函数
  - 5. 假设函数
  - 6. 损失函数
  - 7. 梯度下降算法
  - 8. 可视化模型
  - 9. 模型准确率
  - 10. 试试sklearn库
  - 11. sklearn的准确率
  - 12. 完整程序
二、复杂二分类逻辑回归
- 需求分析
- 程序设计
- - 1. 逻辑回归
  - 2. 模型准确率
  - 3. 增加多项式特征
  - 4. 新的准确率
  - 5. 绘制决策曲线
  - 6. 正则化损失函数
  - 7. 正则化梯度下降函数
  - 8. 试试sklearn库
  - 9. 完整程序
总结

前言

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，所以实际中最为常用的就是二分类的logistic回归，本文主要给出二分类逻辑回归的详细实现过程。

一、普通二分类逻辑回归

需求分析

在训练的初始阶段，我们将要构建一个逻辑回归模型来预测，某个学生是否被大学录取。设想你是大学相关部分的管理者，想通过申请学生两次测试的评分，来决定他们是否被录取。现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本，你有他们两次测试的评分和最后是被录取的结果。

程序设计

1. 导入数据

我们可以使用pandas读取文件中的数据，并给数据添加一个常数列（为了方便计算）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']   #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    #用来正常显示负号
data=pd.read_csv(r"d:/逻辑回归/ex2data1.txt",names=["Exam1","Exam2","Admitted"])
data.insert(0,"ones",1)

2. 可视化数据

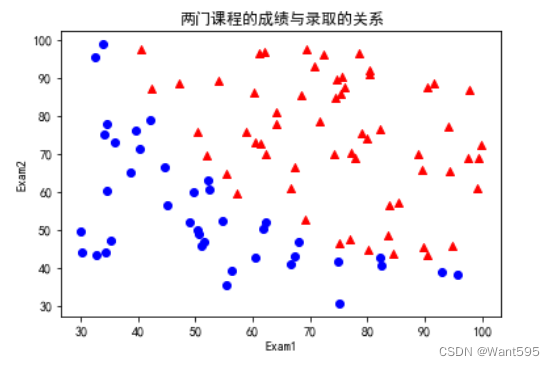
我们可以使用matplotlib来绘制训练集的可视化图形，其中用红色三角形表示被录取的学生，用蓝色圆形表示没有被录取的学生

positive=data["Admitted"].isin([1])
negative=data["Admitted"].isin([0])
plt.scatter(data[positive]["Exam1"],data[positive]["Exam2"],color='red',marker='^')
plt.scatter(data[negative]["Exam1"],data[negative]["Exam2"],color='blue',marker='o')
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.title("两门测试的成绩")
plt.show()

两门课程的成绩与录取的关系图1

3. 划分数据

将数据划分为训练特征和训练标签

m=data.shape[0]
col_num=data.shape[1]
X=data.iloc[:,:col_num-1].values
y=data.iloc[:,col_num-1].values.reshape((m,1))

4. sigmoid函数

我们定义一个sigmoid函数，它将把输入的每个值转换为概率

$g$ 代表一个常用的逻辑函数（logistic function）为 $S$ 形函数（Sigmoid function）

公式为：
$g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$

#sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))

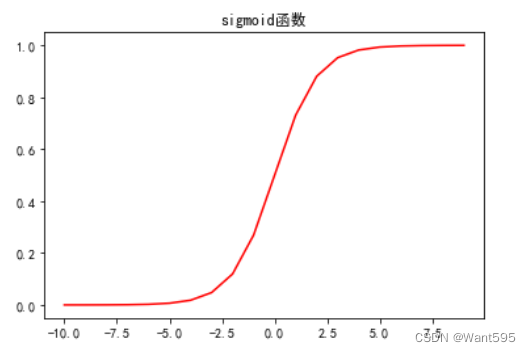
我们可以通过绘图来看看它的正确性

nums=np.arange(-10,10)
fig,ax=plt.subplots(figsize=(6,4))
ax.plot(nums,sigmoid(nums),'r')
plt.show()

没错，是个S型曲线
sigmoid函数

5. 假设函数

我们定义逻辑回归模型，它输出一个由sigmoid函数之后的值构成的矩阵，这代表了每个样本被分配到每个类的概率

由sigmoid函数，我们得到逻辑回归模型的假设函数：
$h\left( x \right)=\frac{1}{1+{{e}^{-{{w }^{T}}x}}}$

#假设函数
def h(X,w):
    return sigmoid(X@w)

6. 损失函数

损失函数：
$J\left(w\right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{({{y}^{(i)}}\log \left( {h}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h}\left( {{x}^{(i)}} \right) \right))}$

我们定义损失函数，用它来度量模型的准确性

#损失函数
def cost(X,w,y):
    return -np.sum(y.ravel()*np.log(h(X,w)).ravel()+(1-y).ravel()*np.log(1-h(X,w)).ravel())/m

7. 梯度下降算法

梯度下降函数：
$\frac{\partial J\left( w \right)}{\partial {{w }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{_{j}}^{(i)}}$

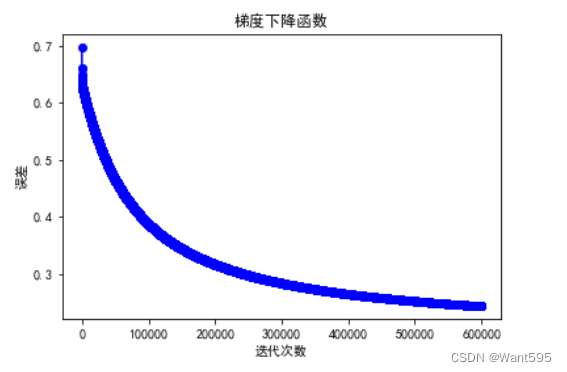
我们使用梯度下降算法来优化成本函数并训练模型
每一次迭代，我们计算每个参数的梯度并更新其值
这个过程重复多次直到损失函数的值越低越好

#梯度下降函数
def gradient_descent(X,w,y,n,a):
    t=w
    cost_lst=[]
    for i in range(n):
        error=h(X,w)-y
        for j in range(col_num-1):
            t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))
        w=t
        cost_lst.append(cost(X,w,y))
    return w,cost_lst
w=np.zeros((col_num-1,1))
n,a=600000,0.001
w,cost_lst=gradient_descent(X,w,y,n,a)
plt.plot(range(n),cost_lst,"b-o")
plt.title("梯度下降函数")
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.show()

梯度下降函数

8. 可视化模型

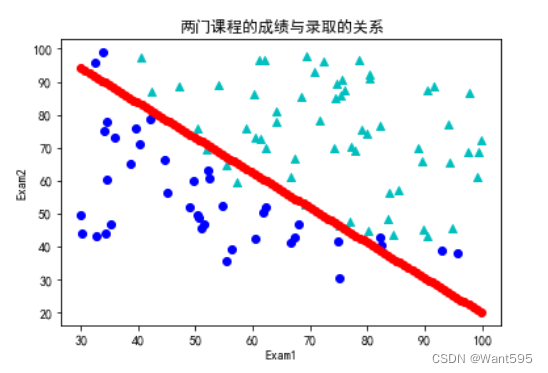
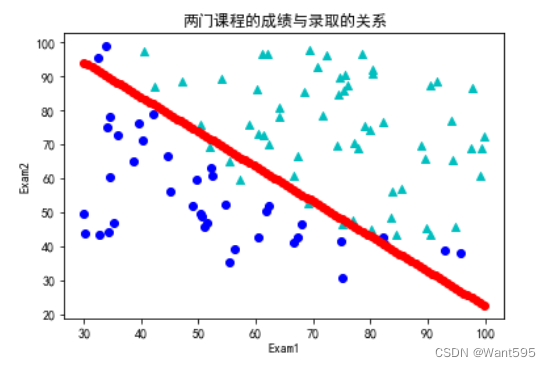
最后，我们可以使用模型来绘制一个决策边界图形，它显示了被录取和没有被录取的学生的分界线

x1=np.linspace(data["Exam1"].min(),data["Exam1"].max(),100)
x2=(-w[0,0]-w[1,0]*x1)/(w[2,0])
plt.plot(x1,x2,"r-o")
plt.scatter(data[positive]["Exam1"],data[positive]["Exam2"],color="c",marker="^")
plt.scatter(data[negative]["Exam1"],data[negative]["Exam2"],color="b",marker="o")
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.title("两门课程的成绩与录取的关系")
plt.show()

两门课程的成绩与录取的关系图2

9. 模型准确率

我们运用该模型进行预测，准确率高达0.9！

Y=(h(X,w)>0.5)
np.sum(y==Y)/m    #输出为0.9

10. 试试sklearn库

导入sklearn库，我们可以快速得到预测结果

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
data=pd.read_csv(r"d:/逻辑回归/ex2data1.txt",names=["Exam1","Exam2","Admitted"])
positive=data["Admitted"].isin([1])
negative=data["Admitted"].isin([0])
X=data.iloc[:,:2].values
y=data.iloc[:,2].values
clf=LogisticRegression()
clf.fit(X,y)
w=clf.coef_[0]
b=clf.intercept_ 
plt.plot(x1,x2,"r-o")
plt.scatter(data[positive]["Exam1"],data[positive]["Exam2"],color="c",marker="^")
plt.scatter(data[negative]["Exam1"],data[negative]["Exam2"],color="b",marker="o")
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.title("两门课程的成绩与录取的关系")
plt.show()

两门课程的成绩与录取的关系图3

11. sklearn的准确率

让我们使用score函数看看准确率如何吧

from sklearn.linear_model import LogisticRegression
y1=y.flatten()
mod = LogisticRegression().fit(X, y1)
mod.score(X,y)            #输出为0.89

准确率高达0.89！

12. 完整程序

完整代码如下

#导入数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']   #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    #用来正常显示负号
data=pd.read_csv(r"d:/逻辑回归/ex2data1.txt",names=["Exam1","Exam2","Admitted"])
data.insert(0,"ones",1)     #插入一列
#可视化数据
positive=data["Admitted"].isin([1])     
negative=data["Admitted"].isin([0])
plt.scatter(data[positive]["Exam1"],data[positive]["Exam2"],color='red',marker='^')
plt.scatter(data[negative]["Exam1"],data[negative]["Exam2"],color='blue',marker='o')
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.title("两门课程的成绩与录取的关系")
plt.show()
#划分数据
m=data.shape[0]
col_num=data.shape[1]
X=data.iloc[:,:col_num-1].values
y=data.iloc[:,col_num-1].values.reshape((m,1))
#sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))
#检验
nums=np.arange(-10,10)
plt.plot(nums,sigmoid(nums),'r')
plt.title("sigmoid函数")
plt.show()
#假设函数
def h(X,w):
    return sigmoid(X@w)
#损失函数
def cost(X,w,y):
    return -np.sum(y.ravel()*np.log(h(X,w)).ravel()+(1-y).ravel()*np.log(1-h(X,w)).ravel())/m
#梯度下降函数
def gradient_descent(X,w,y,n,a):
    t=w
    cost_lst=[]
    for i in range(n):
        error=h(X,w)-y
        for j in range(col_num-1):
            t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))
        w=t
        cost_lst.append(cost(X,w,y))
    return w,cost_lst
w=np.zeros((col_num-1,1))
n,a=600000,0.001
w,cost_lst=gradient_descent(X,w,y,n,a)
plt.plot(range(n),cost_lst,"b-o")
plt.title("梯度下降函数")
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.show()
x1=np.linspace(data["Exam1"].min(),data["Exam1"].max(),100)
x2=(-w[0,0]-w[1,0]*x1)/(w[2,0])
plt.plot(x1,x2,"r-o")
plt.scatter(data[positive]["Exam1"],data[positive]["Exam2"],color="c",marker="^")
plt.scatter(data[negative]["Exam1"],data[negative]["Exam2"],color="b",marker="o")
plt.xlabel("Exam1")
plt.ylabel("Exam2")
plt.title("两门课程的成绩与录取的关系")
plt.show()
Y=(h(X,w)>0.5)
np.sum(y==Y)/m

二、复杂二分类逻辑回归

需求分析

用正则化的Logistic回归模型来预测一个制造工厂的微芯片是否通过质量保证（QA），在QA过程中，每个芯片都会经过各种测试来保证它可以正常运行。假设你是这个工厂的产品经理，你拥有一些芯片在两个不同测试下的测试结果，从这两个测试，你希望确定这些芯片是被接受还是拒绝，为了帮助你做这个决定，你有一些以前芯片的测试结果数据集，从中你可以建一个Logistic回归模型。

程序设计

1. 逻辑回归

像上一个例子一样，运用普通逻辑回归试试

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
datas=pd.read_csv(r"d:/逻辑回归/ex2data2.txt",names=["Test1","Test2","Accepted"])
datas.insert(0,"ones",1)
col_num=datas.shape[1]
m=datas.shape[0]
X=datas.iloc[:,:col_num-1].values
y=datas.iloc[:,col_num-1].values.reshape((m,1))
def sigmoid(z):
    return 1/(1+np.exp(-z))
def h(X,w):
    return sigmoid(X@w)
def cost(X,w,y):
    return -np.sum(y.ravel()*np.log(h(X,w)).ravel()+(1-y).ravel()*np.log(1-h(X,w)).ravel())/m
def gradient_descent(X,w,y,n,a):
    t=w
    cost_lst=[]
    for i in range(n):
        error=h(X,w)-y
        for j in range(col_num-1):
            t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))
        w=t
        cost_lst.append(cost(X,w,y))
    return w,cost_lst

2. 模型准确率

但是我们发现该模型的准确率连0.6都不到

w=np.zeros((col_num-1,1))
n,a=600000,0.001
w,cost_lst=gradient_descent(X,w,y,n,a)
Y=(h(X,w)>=0.5)
np.sum(y==Y)/m    #输出为：0.5508474576271186

3. 增加多项式特征

此时我们需要增加多列多项式的特征

def poly_feature(datas,degree):
    x1=datas["Test1"]
    x2=datas["Test2"]
    for i in range(degree+1):
        for j in range(degree-i+1):
            datas["F"+str(i)+str(j)]=np.power(x1,i)*np.power(x2,j)            
    datas=datas.drop(["Test1","Test2"],axis=1)
    return datas
datas=poly_feature(datas,4)

4. 新的准确率

让我们再来看看模型的准确率如何吧

Y=(h(X,w)>=0.5)
np.sum(y==Y)/m     #输出为：0.847457627118644

准确率达到了0.8，相比0.5很不错啦

5. 绘制决策曲线

让我们一起看看模型的决策曲线图

data=pd.read_csv(r"d:/逻辑回归/ex2data2.txt",names=["Test1","Test2","Accepted"])
x1=np.linspace(-1,1.5,50)
x2=np.linspace(-1,1.5,50)
X1,X2=np.meshgrid(x1, x2)
# 计算每个网格点的预测分类结果
X_grid=poly_feature(pd.DataFrame({"Test1":X1.flatten(),"Test2":X2.flatten()}),degree=4).values
y_grid=h(X_grid,w).reshape(X1.shape)
# 将预测结果转换为0或1，根据阈值0.5进行分类
y_pred=(y_grid>0.5).astype(int)
# 可视化结果
plt.figure(figsize=(8,6))
plt.contourf(X1,X2,y_pred,alpha=0.2,cmap="coolwarm")
plt.scatter(data[positive]["Test1"],data[positive]["Test2"],c="b",marker="o",label="Accepted")
plt.scatter(data[negative]["Test1"],data[negative]["Test2"],c="r",marker="x",label="Not accepted")
plt.xlabel("Test1")
plt.ylabel("Test2")
plt.title("决策曲线图")
plt.legend()
plt.show()

决策曲线图

6. 正则化损失函数

让我们将损失函数正则化一下

def cost_regularization(X,w,y,l):
    cost=-np.sum(y.ravel()*np.log(h(X,w).ravel())+(1-y).ravel()*np.log(1-h(X,w)).ravel())/X.shape[0]+(l/(2*X.shape[0]))*np.sum(np.power(w[1:,0],2))
    return cost

7. 正则化梯度下降函数

再来正则化一下梯度下降函数吧

def grandient_regularization(X,w,y,n,a,l):
    y=y.reshape((X.shape[0],1))
    w=np.zeros((X.shape[1],1))
    cost_lst=[] 
    for i in range(n):
        y_pred=h(X,w)-y
        temp=np.zeros((X.shape[1],1))
        for j in range(0,X.shape[1]):
            if j==0:
                right_0=np.multiply(y_pred.ravel(),X[:,0])
                gradient_0=1/(X.shape[0])*(np.sum(right_0))
                temp[j,0]=w[j,0]-a*(gradient_0)
            else:
                right=np.multiply(y_pred.ravel(),X[:,j])
                reg=(l/X.shape[0])*w[j,0]
                gradient=1/(X.shape[0])*(np.sum(right))
                temp[j,0]=w[j,0]-a*(gradient+reg)          
        w=temp
        cost_lst.append(cost_reg(X,w,y,l))
    return w,cost_lst

8. 试试sklearn库

导入sklearn库，试试直接获取模型的准确率吧

from sklearn import linear_model  #调用sklearn的线性回归包
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X, y.ravel())
model.score(X,y)   #输出为：0.8220338983050848

9. 完整程序

完整代码如下

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']   #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False    #用来正常显示负号
datas=pd.read_csv(r"d:/逻辑回归/ex2data2.txt",names=["Test1","Test2","Accepted"])
#为数据框增加多列多项式特征
def poly_feature(datas,degree):
    x1=datas["Test1"]
    x2=datas["Test2"]
    for i in range(degree+1):
        for j in range(degree-i+1):
            datas["F"+str(i)+str(j)]=np.power(x1,i)*np.power(x2,j)            
    datas=datas.drop(["Test1","Test2"],axis=1)
    return datas
datas=poly_feature(datas,4)
positive=datas["Accepted"]==1
negative=datas["Accepted"]==0
col_num=datas.shape[1]
m=datas.shape[0]
X=datas.iloc[:,1:col_num].values
y=datas.iloc[:,0].values.reshape((m,1))
def sigmoid(z):
    return 1/(1+np.exp(-z))
def h(X,w):
    return sigmoid(X@w)
def cost(X,w,y):
    return -np.sum(y.ravel()*np.log(h(X,w)).ravel()+(1-y).ravel()*np.log(1-h(X,w)).ravel())/m
def gradient_descent(X,w,y,n,a):
    t=w
    cost_lst=[]
    for i in range(n):
        error=h(X,w)-y
        for j in range(col_num-1):
            t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))
        w=t
        cost_lst.append(cost(X,w,y))
    return w,cost_lst
w=np.zeros((col_num-1,1))
n,a=600000,0.001
w,cost_lst=gradient_descent(X,w,y,n,a)
plt.plot(range(n),cost_lst,'b-o')
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.title("误差随迭代次数变化图")
plt.show()
data=pd.read_csv(r"d:/逻辑回归/ex2data2.txt",names=["Test1","Test2","Accepted"])
x1=np.linspace(-1,1.5,50)
x2=np.linspace(-1,1.5,50)
X1,X2=np.meshgrid(x1, x2)
# 计算每个网格点的预测分类结果
X_grid=poly_feature(pd.DataFrame({"Test1":X1.flatten(),"Test2":X2.flatten()}),degree=4).values
y_grid=h(X_grid,w).reshape(X1.shape)
# 将预测结果转换为0或1，根据阈值0.5进行分类
y_pred=(y_grid>0.5).astype(int)
# 可视化结果
plt.figure(figsize=(8,6))
plt.contourf(X1,X2,y_pred,alpha=0.2,cmap="coolwarm")
plt.scatter(data[positive]["Test1"],data[positive]["Test2"],c="b",marker="o",label="Accepted")
plt.scatter(data[negative]["Test1"],data[negative]["Test2"],c="r",marker="x",label="Not accepted")
plt.xlabel("Test1")
plt.ylabel("Test2")
plt.title("决策曲线图")
plt.legend()
plt.show()