【LeetCode: 面试题 08.01. 三步问题 | 暴力递归=＞记忆化搜索=＞动态规划】

🍎作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🍎座右铭：人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯🎯

题目链接

面试题 08.01. 三步问题

题目描述

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

示例1:
输入：n = 3
输出：4
说明: 有四种走法

示例2:
输入：n = 5
输出：13

提示:
n范围在[1, 1000000]之间

求解思路&实现代码&运行结果

暴力递归

求解思路

实现代码

class Solution {

    public final int mod=1000000007;

    public int waysToStep(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        if(n==3) return 4;
        return (waysToStep(n-1)%mod+waysToStep(n-2)%mod+waysToStep(n-3)%mod)%mod; 
    }
}

运行结果

根据我们代码提交的结果来看，不出我们所料，直接时间超限，但是所有的事情并不是绝对的，或者都是坏的，都是好的，虽然时间超限，但是侧面验证了我们的思路是正确的，对吧，接下来我们就有大致的改进方向了。

记忆化搜索

求解思路

1. 根据我们递归的分析，在递归的过程中会产生重复的子过程，为了改进这个过程，避免重复计算的问题，此时我们想到的解决方案就是加一个缓存表，也就是我们的记忆化搜索。
2. 具体实现的相关细节请看具体的代码。

实现代码

class Solution {

    public final int mod=1000000007;
    
    public int waysToStep(int n) {
        long[] dp=new long[1000010];
        return (int)(waysToStep(n,dp)); 
    }

    public long waysToStep(int n,long[] dp) {
        if(dp[n]!=0) return dp[n];
        if(n==1) return dp[n]=1;
        if(n==2) return dp[n]=2;
        if(n==3) return dp[n]=4;
        return dp[n]=(waysToStep(n-1,dp)%mod+waysToStep(n-2,dp)%mod+waysToStep(n-3,dp)%mod)%mod; 
    }
}

运行结果

之前的暴力递归过都过不了，此时我们可以看到记忆化缓存已经可以勉强通过了，撒花啦。。。
但是，有的同学可不想止步于此呢？那么怎么做呢？我们就需要继续进行改进了，也就是接下来的动态规划版本。

动态规划

求解思路

1. 那动态规划怎么做呢？怎么改进呢？接下来我们就要根据这个递归的过程去求解动态规划的递推公式，也就是我们常说的状态转移。
2. 具体过程如下图所示:
   

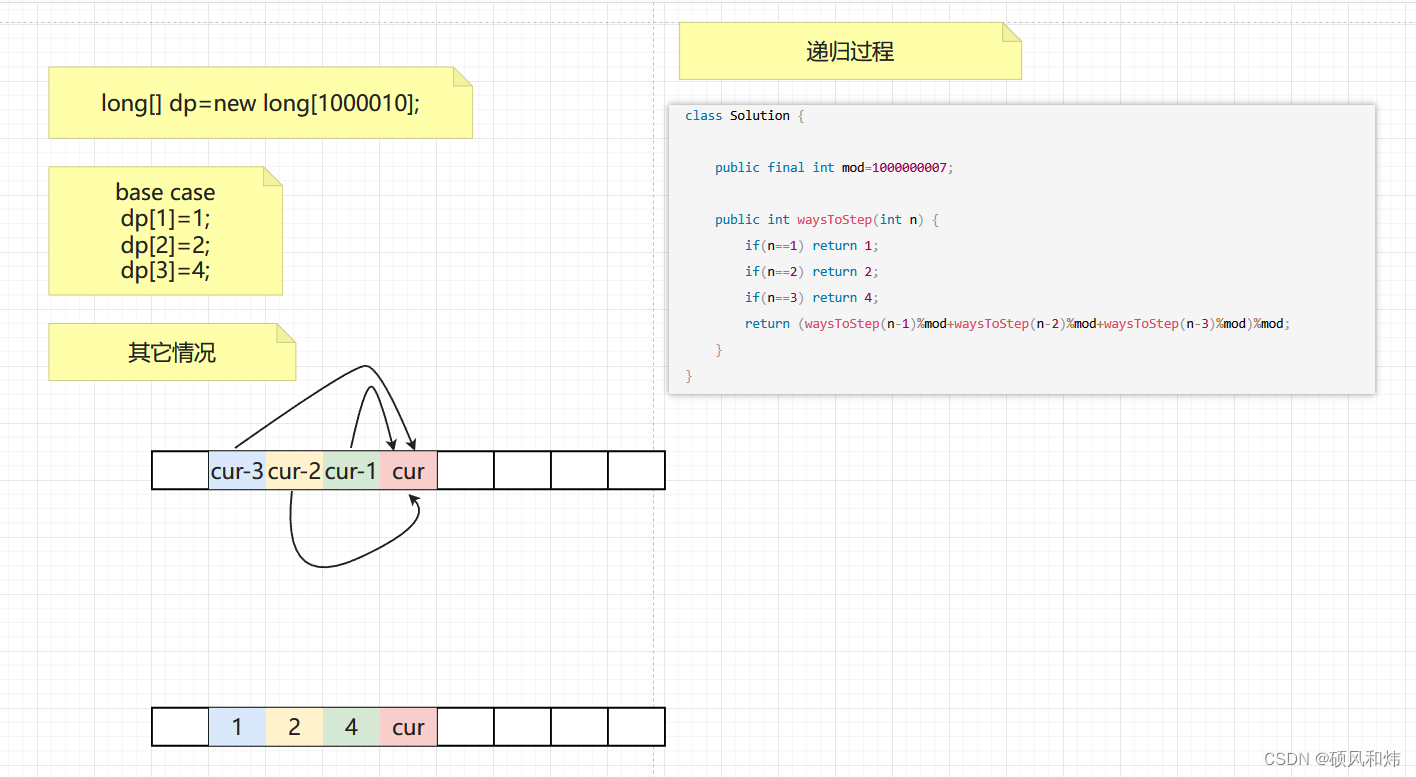
实现代码

class Solution {

    public final int mod=1000000007;
    
    public int waysToStep(int n) {
        long[] dp=new long[1000010];
        dp[1]=1;
        dp[2]=2;
        dp[3]=4;
        for(int i=4;i<=n;i++){
            dp[i]=(dp[i-1]%mod+dp[i-2]%mod+dp[i-3]%mod)%mod;
        }
        return (int)(dp[n]); 
    }

}

运行结果

此时呢，最终的动态规划的版本就出来了，大家可以看到，一步一步走来有理有据，比起我们直接去想这个最终的动态规划是不是更好理解呢？

课后任务

虽然上面我们已经求得了最终的动态规划，此时的时间复杂度已经达到最优了O(n),但是大家有没有发现一个问题，此时的空间复杂度还是可以继续进行优化的，优化的方法是什么呢？也就是我们常说的状态压缩,那么这个任务就留给你了，下来一定要动手亲自实操一下，把它实现,我把代码贴到这里，大家可以参考一下。

状态压缩

class Solution {

    public final int mod=1000000007;
    
    public int waysToStep(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        if(n==3) return 4;
        long a=1,b=2,c=4;
        long ans=0;
        for(int i=4;i<=n;i++){
            ans=(a%mod+b%mod+c%mod)%mod;
            a=b;
            b=c;
            c=ans;
        }
        return (int)(ans); 
    }

}

运行结果

共勉

最后，我想送给大家一句一直激励我的座右铭，希望可以与大家共勉！