【LeetCode】剑指 Offer 44. 数字序列中某一位的数字 p225 -- Java Version
题目链接:https://leetcode.cn/problems/shu-zi-xu-lie-zhong-mou-yi-wei-de-shu-zi-lcof/
1. 题目介绍(44. 数字序列中某一位的数字)
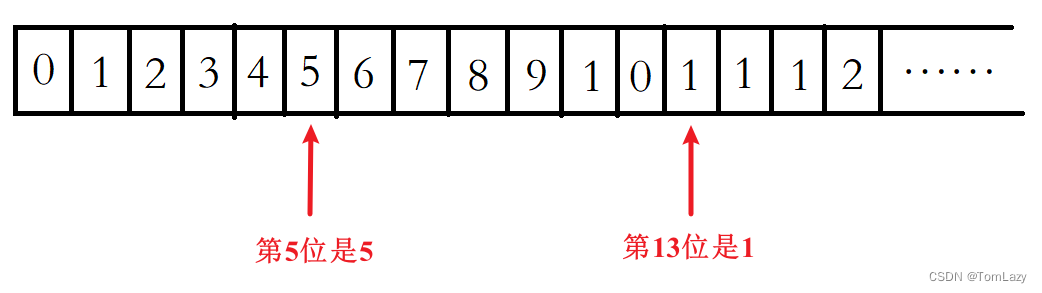
数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从下标0开始计数)是5,第13位是1,第19位是4,等等。
请写一个函数,求任意第n位对应的数字。
【测试用例】:
示例1:
输入:n = 3
输出:3
示例2:
输入:n = 11
输出:0
【条件约束】:
限制:
- 0 <= n < 2^31
【相关题目】:
注意:本题与主站 400. 第 N 位数字 题目相同。
2. 题解
2.1 枚举 – O(n)
时间复杂度O(n),空间复杂度O(n)
【解题思路】:
从0开始逐一枚举每个数字。每枚举一个数字的时候,求出该数字是几位数(如15是2位数、9323是4位数),并把该数字的位数和前面所有数字的位数累加。如果位数之和仍小于或等于输入n,则继续枚举下一个数字。当累加的数位大于n时,那么第n位数字一定在这个数字里,我们再从该数字中找出对应的那一位。
……
【实现策略】:
- 定义累加位数和
idx,用来存储到入参n所对应数字的总位数;- 从 1 开始循环累加,通过
Math.log10()方法来求当前数字有多少位,并加入到idx中;- 一旦累加位数和的值 大于了 入参位数
n, 那么就说明当前i即为n所对应的数字,- 开始寻找 n 在对应数字中所对应的位置,
c = n - (idx + 1 - str.length());- 找到之后,返回结果。
class Solution {
// Solution1:枚举
// 思路:遍历每一个数字,计算其位数,然后累加
public int findNthDigit(int n) {
// 定义累加位数和
int idx = 0;
for (int i = 1; i <= n; i++) {
// 一旦累加位数和的值 大于了 入参位数 n, 那么就说明当前 i 即为 n 所对应的数字
// 下面我们只要找到 n 在该数字对应哪一位即可
// Math.log10():用来求当前数字有多少位,因为对数函数中 X 不能等于 0, 所以我们跳过了0;
// 改为了 idx 与 n-1 进行比较
idx += (int)Math.log10(i)+1;
if (idx > n-1) {
// 将数字 i 转化成字符串形式,方便操作
String str = String.valueOf(i);
// n 在 该数字处于的位数 = (当前数字的总位数 - n - 该数字的位数)的绝对值
// 以 n = 77 为例:对应的数字为 43,此时总位数 = 10 + 34 * 2 = 78 (idx+1)
// 总位数 - 该数字的位数 = 78 - 2 = 0 ~ 上一个数字的总位数
// 此时,用 n - 上一个数字的总位数 = n 在对应数字的对应位置
int c = n - (idx + 1 - str.length());
return str.charAt(c)-'0';
}
}
// 正常情况下以下代码不会执行
System.out.println(idx);
return 0;
}
}
2.2 补位求余 – O(logn)
时间复杂度O(logn),空间复杂度O(1)
【解题思路】:
- 参考题解:最简洁思路 & 5行代码 – 青云柒
……
思路:主要是用到了一些数学思想,即将每个数字字符宽度都补成当前位数i, 那么返回下标k//i的数 的 第k%i位即可
·
核心:就是通过 补位 的方法,推导出经过补位后(i为最终每个数字的位数)求第n位的公式:(n / i)[n % i]。
……
【实现策略】:
如下方代码注释所示。
class Solution {
public int findNthDigit(int n) {
// 将 n 赋值给 k
long k = n;
// i 表示位数:
// 当 i = 1 时,表示 0 ~ 9,共有10个位数
// 当 i = 2 时,表示 10 ~ 99,共有 200 = 90 * 2 + 20 (0 ~ 9在此时被补成2位的位数)
// 当 i = 3 时,表示 100 ~ 999,共有 3000 = 900 * 3 + 100 * 3 (0 ~ 99范围 100个数被补成3位的位数)
// 当 i = 4 时,表示 1000 ~ 9999,共有 40000 = 9000 * 4 + 1000 * 4
// ……
// 依次类推,我们就得到了一个规律:即,当前位的总位数 = 位数 * (0 ~ 最大位数字)的数量 = i * pow(10,i);
for(int i = 1; ; i++) {
if (i * Math.pow(10, i) > k) {
// 因为是对原数字补i位,就相当于每个真实数字都是以i位进行分隔,那么让 总位数 / 位数 就可以找到 对应数字
String s = k / i + "";
System.out.println(s);
// 然后再对位数取余,就得到了 题目要求返回的那一位
return s.charAt((int)(k % i))-'0';
}
// 总位数 = 原位数 + 新增位数
// 这里的总位数表示:补位之后,到n位所在数字的所有位数 (特别提示:入参 n 代表的是位数,而不是数字!)
// 以 k = 103 为例,对应的数字为 56 = 2 * 57 = 114 (全部补位后)
// k = 103 + 10 = 113 (这样通过 k // 2 就确定了数字 56)
// 再通过对位数取余 (k % 2 = 113 % 2 = 1)确定了要返回的位数在56中的位置
k += Math.pow(10, i);
}
}
}
2.3 迭代 + 求整 / 求余 – O(logn)
时间复杂度O(logn),空间复杂度O(logn)
【解题思路】:
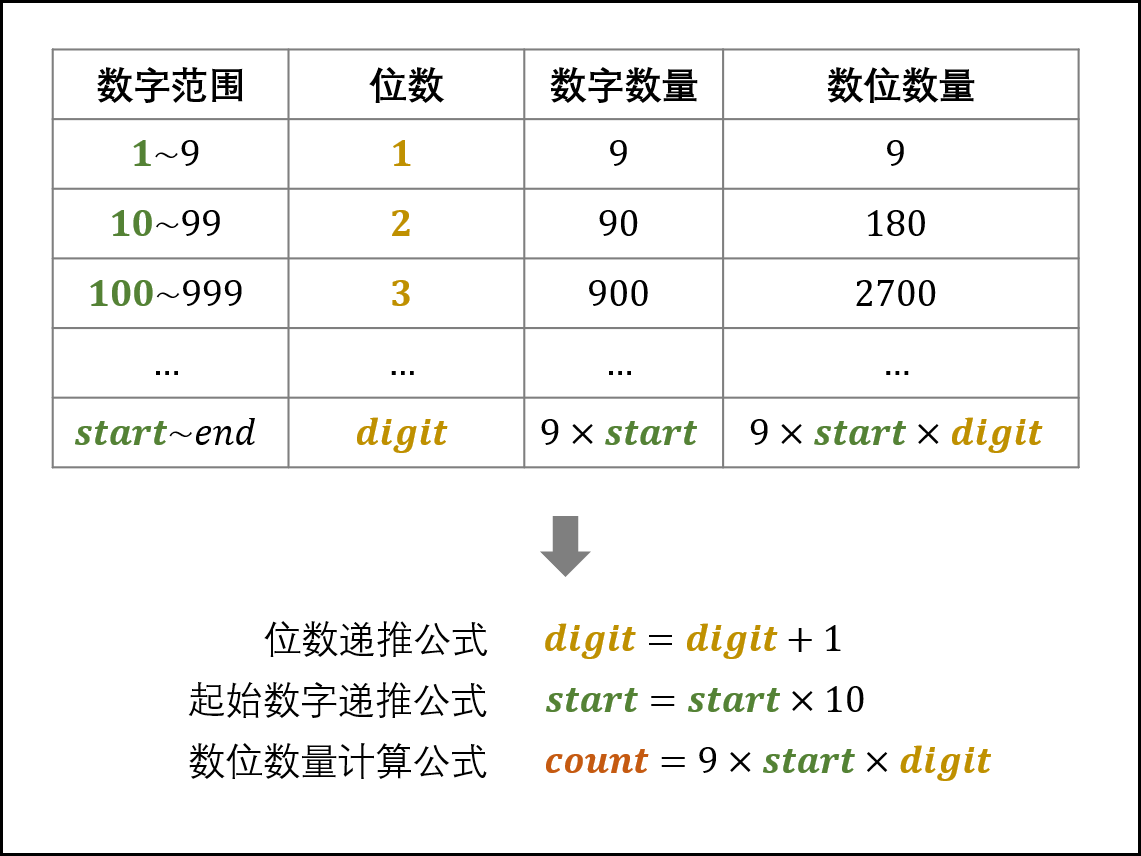
该方法与 2.2 补位求余思想类似:
class Solution {
public int findNthDigit(int n) {
int digit = 1;
long start = 1;
long count = 9;
while (n > count) { // 1.
n -= count;
digit += 1;
start *= 10;
count = digit * start * 9;
}
long num = start + (n - 1) / digit; // 2.
return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.
}
}
3. 参考资料
[1] 面试题44. 数字序列中某一位的数字(迭代 + 求整 / 求余,清晰图解)

