Stata 回归结果详解
目录
- 一、数据信息
- 二、指标
- 1.上半部分
- 2.下半部分
- 三、详细解释
- SSM - 模型平方和
- SSR - 残差平方和
- SST - 总平方和
- R-squared - R方 - 拟合系数
- Adj R-squared - 调整后的拟合系数
- df - 自由度
- MS - 均方差
- F - 总体显著性检验
- Prob > F - P值
- Root MSE
- Coef.
- Std. Err.
- t
- P > | t |
- 95% Conf. Interval
一、数据信息
使用stata自带的auto数据,
被解释变量(因变量):price(价格)
解释变量(自变量):mpg(里程)、rep78(1978年后的修理记录)、weight(重量)、length(长度)、foreign(本土/国外品牌)
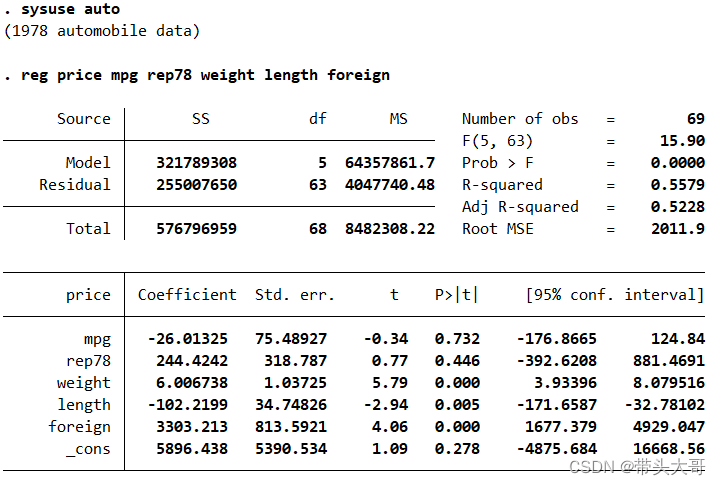
回归结果分两部分,上半部分为回归结果的总体描述信息,下半部分为具体变量信息。
二、指标
1.上半部分
| 指标 | 英文 | 名称 | 解释 |
|---|---|---|---|
| SS | sum of squares | 平方和 | |
| df | degrees of freedom | 自由度 | |
| MS | mean square | 均方差 | |
| Model(SSM) | sum of squares model | 模型平方和 | 衡量预测值的离散程度 |
| Residual(SSR) | sum of squares residual | 残差平方和 | 衡量预测值与真实值的偏差程度 |
| Total(SST) | sum of squares total | 总平方和 | 衡量真实数据的离散程度 |
| Number of obs | 观测值数量 | 观测值数量 | |
| F(a,b) | F值 | 检验系数不为0的概率 | |
| Prob > F | P值 | 1%、5%、10%水平上显著 | |
| R-squared | 拟合系数 | 表示模型的拟合程度 | |
| Adj R-squared | 调整后的拟合系数 | 更精确的表示模型的拟合程度 | |
| Root MSE | Root Mean square of error | 均误差平方根 | 衡量模型中的误差项的大小 |
2.下半部分
| 指标 | 英文名 | 中文名 | 解释 |
|---|---|---|---|
| Coefficient | 系数 | β | |
| Std. err. | The standard error of the coefficient | 回归系数标准误 | 估计系数的波动水平 |
| t | t值 | 检验系数不为0的概率 | |
| p > [t] | P值 | 1%、5%、10%水平上显著 | |
| [95% conf. interval] | confidence interval | 置信区间 | 回归系数取值范围,该范围有效率是95% |
三、详细解释
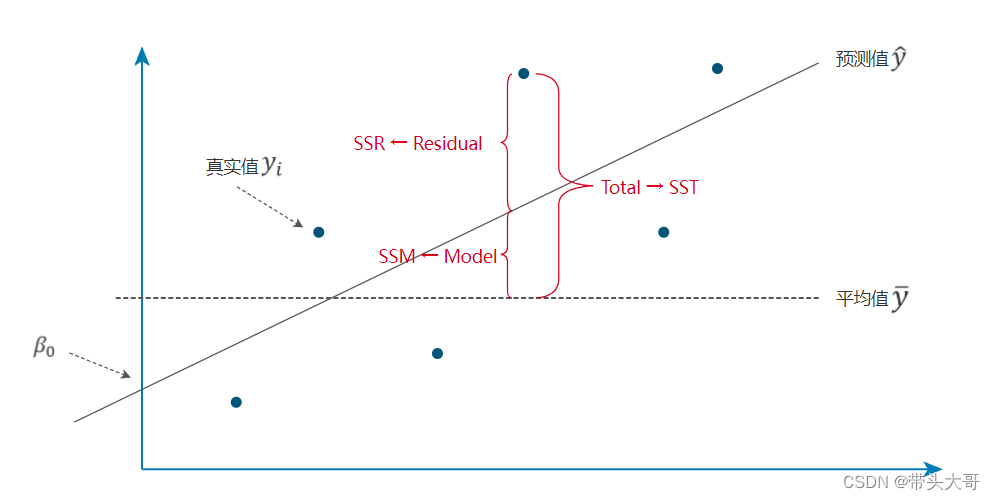
SSM - 模型平方和
每一个预测值与平均值之间距离的平方之和
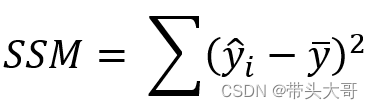
SSM越大越好
SSR - 残差平方和
每一个真实值与预测值之间距离的平方之和,即误差项的平方和
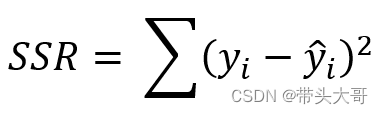
SSR越小越好
SST - 总平方和
每一个真实值与平均值之间距离的平方之和,用于衡量真实值的离散程度
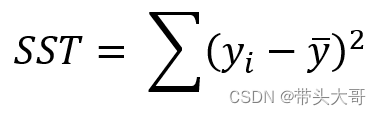
SST = SSM + SSR ,即【总平方和=模型平方和+残差平方和】
R-squared - R方 - 拟合系数
拟合系数表示模型能解释的数据波动占总体波动的百分比,表示拟合程度
R方越高,表示模型的拟合程度越高,回归预测越准确
R方的值在0到1之间,具体的大小并无要求,需要根据不同的领域具体判断,在某些领域,10%-30%是合理的;而在某些领域甚至达到50%才是合理。
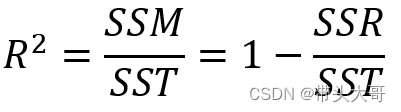
Adj R-squared - 调整后的拟合系数
R-squared无法控制变量的增加而导致过度拟合,Adj R-squared则在此基础上,引入了自变量的个数这一因素,以更加准确地评估模型的拟合效果。
在多元线性回归模型中,当自变量的数量增加时,R-squared也会随之增加。但是,当自变量的数量增加时,也容易出现过拟合(overfitting)现象,导致模型的预测能力下降。因此,为了避免过拟合,我们需要使用Adj R-squared对R-squared进行修正。Adj R-squared可以更精确地反映自变量对因变量的解释程度,避免了因自变量数量增加而导致的过拟合问题,是多元线性回归模型中一个比较重要的评估指标。
df - 自由度
自由度是表示能够自由变动的变量的个数
例如:有3个变量a、b、c,加入限制条件 a + b + c = 100,则a和b任意取一个值后,c无法自由取值,即df=2。
在本文章的数据中,观测值 n= 69,自由度 df = 69 - 1 = 68
本章数据中,假设观测值个数为n,自变量个数为k,则:
df_Total = n - 1
df_Model = k (不是k-1,因为模型中有常数项β0,所以模型的自由度就是自变量个数)
df_Residual = n - k -1 = 69 - 5 - 1 = 63
MS - 均方差
MS = SS / df
简单理解就是平方和的平均数
F - 总体显著性检验
F = MS_Model / MS_Residual
原假设H0:所有系数β均为0
备择假设H1:系数β不全为0
F值越大越好
Prob > F - P值
P值表示在在原假设成立的情况下,能够得到F值的概率,通常有模型在1%、5%、10%水平下拒绝原假设,从而认为自变量对因变量影响的显著水平,也可以说模型在1%、5%、10%水平上显著。
P值由F值查表得出
P值表示在在原假设成立的情况下,能够得到F值的概率,通常有模型在1%、5%、10%水平下拒绝原假设,从而认为自变量对因变量影响的显著水平,也可以说模型在1%、5%、10%水平上显著。
当 P < 0.1 时,模型在10%水平上显著。
当 P < 0.05 时,模型在5%水平上显著。
当 P < 0.01 时,模型在1%水平上显著。
P值越小越好
Root MSE
衡量模型中的误差项的大小,Root MSE越大,误差越大
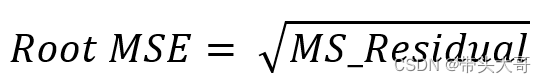
Root MSE越小越好
Coef.
回归系数,其中_cons表示常数项
例:连续变量和0-1变量的解释不用,本文数据中:
车辆重量weight为连续变量,weight每增加一千克,价格price将增加6.006738美元。
是否为外国车辆foreign为0-1变量,当foreigh=1时,价格price将增加3303.213美元。
Std. Err.
衡量估计系数的波动水平
t
t = Coef. / Std. Err.
越大越好
P > | t |
仍是P值,根据t值查表获得
当 | t | > 1.65 或 P < 0.1 时,模型在10%水平上显著,标记*。
当 | t | > 1.96 或 P < 0.05 时,模型在5%水平上显著,标记**。
当 | t | > 2.58 或 P < 0.01 时,模型在1%水平上显著,标记***。
越小越好
95% Conf. Interval
95%置信区间,表示回归系数的取值范围,该范围有效的概率是95%
