聚类问题的算法总结
目录
一、K-means算法
1、算法原理
2、如何确定K值
3、算法优缺点
二、DBScan聚类
1、算法原理
2、处理步骤
3、算法优缺点
聚类代码实现
聚类算法属于无监督学习,与分类算法这种有监督学习不同的是,聚类算法事先并不需要知道数据的类别标签,而只是根据数据特征去学习,找到相似数据的特征,然后把已知的数据集划分成几个不同的类别。
一、K-means算法
1、算法原理
假设我们的数据 总共有 m 条,我们计划分为 3 个类别。如果我们的数据有两个特征维度,那我们的数据就分布在一个 二维平面上,如果有十个维度,就分布在一个十维的空间中。

第一轮,先随机在这个空间中选取三个点,我们称之为中心点,当然选取的三个点不一定是实际的数据点。接着计算所有的点到这三个点的距离,这里的距离计算仍然使用的是欧氏距离,每个点都选择距离 最近的那个作为自己的中心点。这个时候我们就已经把数据划分成了三个组。使用每个组的数据计算出 这些数据的一个均值,使用这个均值作为下一轮迭代的中心点。 后面若干轮重复上面的过程进行迭代,当达到一些条件,比如说规定的轮次或者中心点的变动很小等, 就可以停止运行了。
2、如何确定K值
有一个比较常用的方法,叫作手肘法。
就是去循环尝试 K 值,计算在不同的 K 值情况下,所有数据的损 失,即用每一个数据点到中心点的距离之和计算平均距离。可以想到,当 K=1 的时候,这个距离和肯定 是最大的;当 K=m 的时候,每个点也是自己的中心点,这个时候全局的距离和是 0,平均距离也是 0, 当然我们不可能设置成 K=m。 而在逐渐加大 K 的过程中,会有一个点,使这个平均距离发生急剧的变化,如果把这个距离与 K 的关系 画出来,就可以看到一个拐点,也就是我们说的手肘。
3、算法优缺点
优点
- 简洁明了,计算复杂度低。 K-means 的原理非常容易理解,整个计算过程与数学推理也不是很困 难。
- 收敛速度较快。 通常经过几个轮次的迭代之后就可以获得还不错的效果。
缺点
- 结果不稳定。 由于初始值随机设定,以及数据的分布情况,每次学习的结果往往会有一些差异。
- 无法解决样本不均衡的问题。 对于类别数据量差距较大的情况无法进行判断。
- 容易收敛到局部最优解。 在局部最优解的时候,迭代无法引起中心点的变化,迭代将结束。
- 受噪声影响较大。 如果存在一些噪声数据,会影响均值的计算,进而引起聚类的效果偏差。
二、DBScan聚类
1、算法原理
对于一个已知的点,以它为中心,以给定的半径画一个圆,落在这个圆内的就是与当前点比较紧密的 点;而如果在这个圆内的点达到一定的数量,即达到最少样本量,就可以认为这个区域是比较稠密的。 在算法的开始,要给出半径和最少样本量,然后对所有的数据进行初始化,如果一个样本符合在它的半 径区域内存在大于最少样本量的样本,那么这个样本就被标记为核心对象。
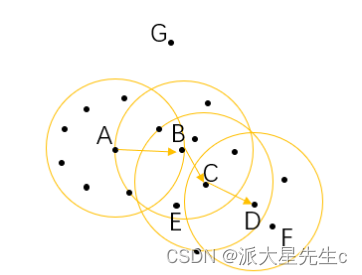
对于在整个样本空间中的样本,可以存在下面几种关系:
- 直接密度可达: 如果一个点在核心对象的半径区域内,那么这个点和核心对象称为直接密度可达,比如 上图中的 A 和 B 、B 和 C 等。
- 密度可达: 如果有一系列的点,都满足上一个点到这个点是密度直达,那么这个系列中不相邻的点就称 为密度可达,比如 A 和 D。
- 密度相连: 如果通过一个核心对象出发,得到两个密度可达的点,那么这两个点称为密度相连,比如这 里的 E 和 F 点就是密度相连。
2、处理步骤
- 经过了初始化之后,再从整个样本集中去抽取样本点,如果这个样本点是核心对象,那么从这个点出 发,找到所有密度可达的对象,构成一个簇。
- 如果这个样本点不是核心对象,那么再重新寻找下一个点。
- 不断地重复这个过程,直到所有的点都被处理过。
- 这个时候,我们的样本点就会连成一片,也就变成一个一个的连通区域,其中的每一个区域就是我们所 获得的一个聚类结果。
- 当然,在结果中也有可能存在像 G 一样的点,游离于其他的簇,这样的点称为异常点。
3、算法优缺点
优点
- 不需要划分个数。 跟 K-means 比起来,DBSCAN 不需要人为地制定划分的类别个数,而可以通 过计算过程自动分出。
- 可以处理噪声点。 经过 DBSCAN 的计算,那些距离较远的数据不会被记入到任何一个簇中,从而 成为噪声点,这个特色也可以用来寻找异常点。
- 可以处理任意形状的空间聚类问题。 从我们的例子就可以看出来,与 K-means 不同,DBSCAN
- 可以处理各种奇怪的形状,只要这些数据够稠密就可以了。
缺点
- 需要指定最小样本量和半径两个参数。 这对于开发人员极其困难,要对数据非常了解并进行很好 的数据分析。而且根据整个算法的过程可以看出,DBSCAN 对这两个参数十分敏感,如果这两个 参数设定得不准确,最终的效果也会受到很大的影响。
- 数据量大时开销也很大。 在计算过程中,需要对每个簇的关系进行管理。所以当数据量大的话, 内存的消耗也非常严重。
- 如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差。
聚类代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles,make_blobs,make_moons
from sklearn.cluster import KMeans,DBSCAN,AgglomerativeClustering
n_samples=1000
circles=make_circles(n_samples=n_samples,factor=0.5,noise=0.05)
moons=make_moons(n_samples=n_samples,noise=0.05)
blobs=make_blobs(n_samples=n_samples,random_state=8,center_box=(-1,1),cluster_std=0.1)
random_data=np.random.rand(n_samples,2),None
colors="bgrcmyk"
data=[circles,moons,blobs,random_data]
models=[("None",None),("Kmeans",KMeans(n_clusters=3)),
("DBSCAN",DBSCAN(min_samples=3,eps=0.2)),
("Agglomerative",AgglomerativeClustering(n_clusters=3,linkage="ward"))]
from sklearn.metrics import silhouette_score
f=plt.figure()
for inx,clt in enumerate(models):
clt_name,clt_entity=clt
for i,dataset in enumerate(data):
X,Y=dataset
if not clt_entity:
clt_res=[0 for item in range(len(X))]
else:
clt_entity.fit(X)
clt_res=clt_entity.labels_.astype(np.int)
f.add_subplot(len(models),len(data),inx*len(data)+i+1)
#plt.title(clt_name)
try:
print(clt_name,i,silhouette_score(X,clt_res))
except:
pass
[plt.scatter(X[p,0],X[p,1],color=colors[clt_res[p]]) for p in range(len(X))]
plt.show()