【LeetCode每日一题: 516. 最长回文子序列 | 暴力递归=＞记忆化搜索=＞动态规划 | 区间dp 】

🍎作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🍎座右铭：人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯🎯

题目链接

516. 最长回文子序列

题目描述

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：
输入：s = “bbbab”
输出：4
解释：一个可能的最长回文子序列为 “bbbb” 。

示例 2：
输入：s = “cbbd”
输出：2
解释：一个可能的最长回文子序列为 “bb” 。

提示：

1 <= s.length <= 1000
s 仅由小写英文字母组成

求解思路&实现代码&运行结果

暴力递归

求解思路

1. 为了能够让同学们更好的理解这个过程，我特意将整个思考的过程以及作图的过程都绘制在下面这张图中，希望可以通过下面这张图更好的帮助你理解整个过程，大家可以结合这张图来理解整个题目的求解思路。
   

实现代码

注意，代码的实现方式可以有很多，大家根据自己的习惯来就好

class Solution {
    public int longestPalindromeSubseq(String s) {
        if(s==null||s.length()<=0) return 0;
        int n=s.length();
        return process(0,n-1,s);
    }

    public int process(int left,int right,String s){
        if(left==right) return 1;
        if(left>right) return 0;
        if(s.charAt(left)==s.charAt(right)){
            return process(left+1,right-1,s)+2;
        }
        return Math.max(process(left+1,right,s),process(left,right-1,s));
    }
}

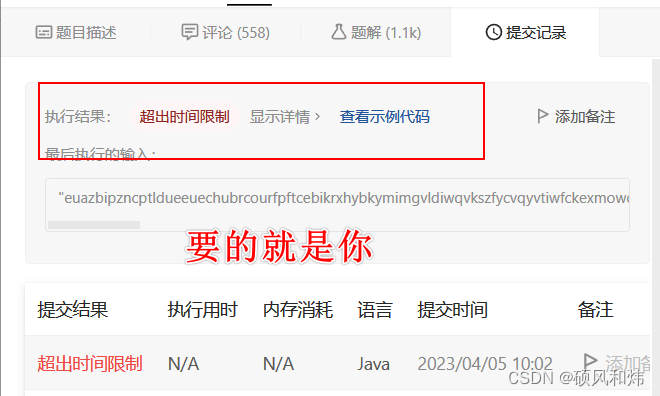
运行结果

大家不要看到时间超限就害怕，相反，看到这个我们更应该放心，使我们期待的结果。

记忆化搜索

求解思路

1. 核心思路就是我们上面的求解过程，如果没有理解可以继续看上面的图解过程。
2. 在原来的基础上加缓存表，将结果进行记录，避免重复计算。

实现代码

class Solution {
    public int longestPalindromeSubseq(String s) {
        if(s==null||s.length()<=0) return 0;
        int n=s.length();
        int[][] dp=new int[n][n];
        for(int i=0;i<n;i++) Arrays.fill(dp[i],-1);
        return process(0,n-1,s,dp);
    }

    public int process(int left,int right,String s,int[][] dp){
        if(dp[left][right]!=-1) return dp[left][right];
        if(left==right) return dp[left][right]=1;
        if(left>right) return dp[left][right]=0;
        if(s.charAt(left)==s.charAt(right)){
            return dp[left][right]=process(left+1,right-1,s,dp)+2;
        }
        return dp[left][right]=Math.max(process(left+1,right,s,dp),process(left,right-1,s,dp));
    }
}

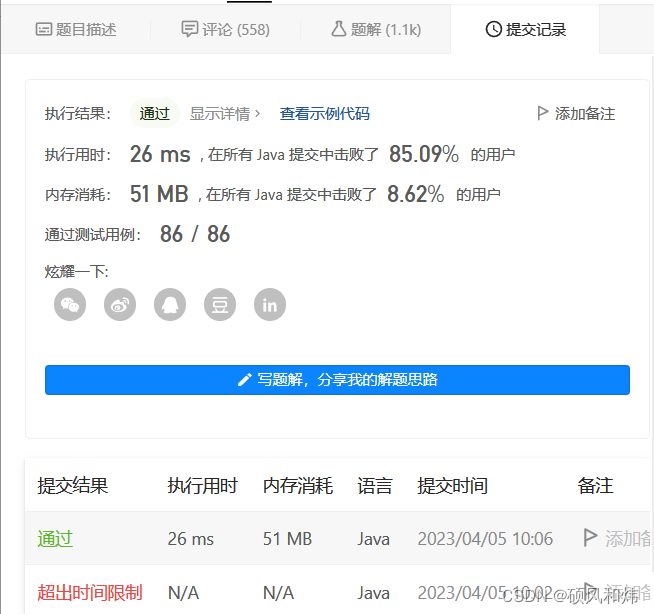
运行结果

加个缓存表就是香，通过！

动态规划

求解思路

1. 同理，核心求解思路我们上面已经讲过了，此处不同的是原来通过递归，此时我们通过dp数组和循环即可完成。

实现代码

继续改进！

class Solution {
    public int longestPalindromeSubseq(String s) {
        if(s==null||s.length()<=0) return 0;
        int n=s.length();
        int[][] dp=new int[n][n];
        for(int i=0;i<n;i++) dp[i][i]=1;
        for(int left=n-1;left>=0;left--){
            for(int right=left+1;right<n;right++){
                if(s.charAt(left)==s.charAt(right)){
                    dp[left][right]= dp[left+1][right-1]+2;
                }else{
                    dp[left][right]=Math.max(dp[left+1][right],dp[left][right-1]);
                }
            }
        }
        return dp[0][n-1];
    }
}

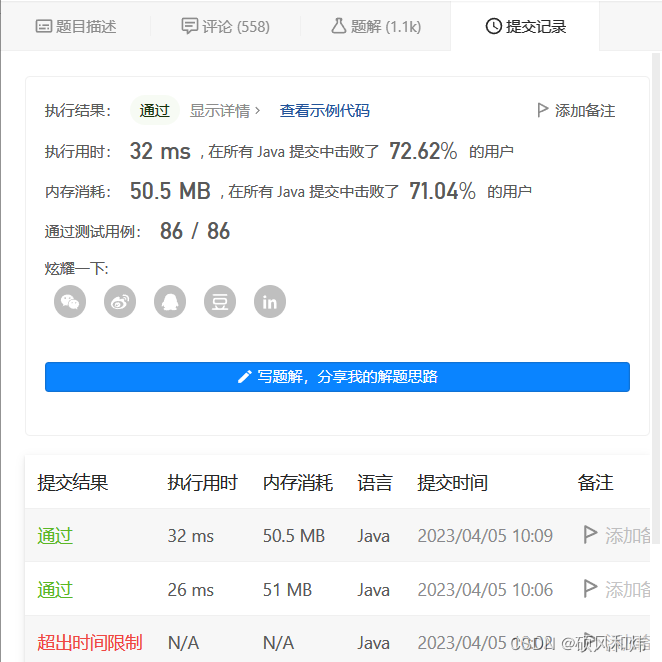
运行结果

共勉

最后，我想送给大家一句一直激励我的座右铭，希望可以与大家共勉！