题目链接：https://leetcode.cn/problems/chou-shu-lcof/

1. 题目介绍（49. 丑数）

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

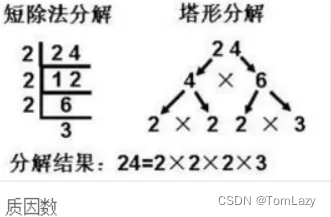
质因数：质因子（或质因数）在数论里是指能整除给定正整数的质数。根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。
……

【测试用例】：
示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

【条件约束】：

说明:

• 1 是丑数。
• n 不超过1690。

【相关题目】：

注意：本题与主站 264. 丑数 II 题目相同

2. 题解

2.1 枚举 – O(n²)

时间复杂度 O(n^2^): 该算法中有一个while循环，在最坏情况下，需要遍历到第n个丑数才能返回结果。对于每个数，需要判断是否是丑数。判断是否是丑数需要多次除以2、3、5，但每个数只会除以一定数量的2、3、5，因此这个过程的时间复杂度可以看作是O(1)。因此，整个算法的时间复杂度为O(n^2)

空间复杂度O(1)：该算法没有使用任何额外空间，只使用了常数级别的额外空间来保存一些变量，因此空间复杂度为O(1)

【解题思路】：
逐个判断每个整数是不是丑数。所谓一个数 m 是另外一个数 n 的因子，是指 n 能被 m 整除，也就是 n%m == 0。根据丑数的定义，丑数只能被 2、3 和 5 整除。也就是说，如果一个数能被 2 整除，就连续除以 2； 如果能被 3 整除，就连续除以 3；如果能被 5 整除，就连续除以 5。如果最后得到的是 1，那么这个数就是丑数；否则不是。
……
【实现策略】：

1. 定义变量 uglyCount 用来记录当前找到的丑数个数；
2. 定义方法 isUgly() 用来判断一个数是不是丑数；
3. 从 0 开始循环判断当前 i 是不是丑数，直到找到的丑数个数为 n；
4. 返回结果。

class Solution {
    // Solution1：枚举
    public int nthUglyNumber(int n) {
        // 无效输入判断
        if (n <= 0) return 0;
        // 保存找到的丑数个数 
        int uglyCount = 0;
        // 从 0 开始判断丑数
        int i = 0;
        while (uglyCount < n) {
            i++;
            if (isUgly(i)) uglyCount++;
        }
        return i;
    }
    // 判断一个数是否为丑数
    public boolean isUgly(int num) {
        while (num % 2 == 0) num /= 2;
        while (num % 3 == 0) num /= 3;
        while (num % 5 == 0) num /= 5;
        return (num == 1)? true : false;
    }
}

2.2 动态规划（原书题解思想） – O(n)

时间复杂度O(n)，空间复杂度O(n)

【解题思路】：
使用 动态规划 思想实现的方法来寻找第 n 个丑数的算法，其中 ugly[i] 表示第 i 个丑数。
……
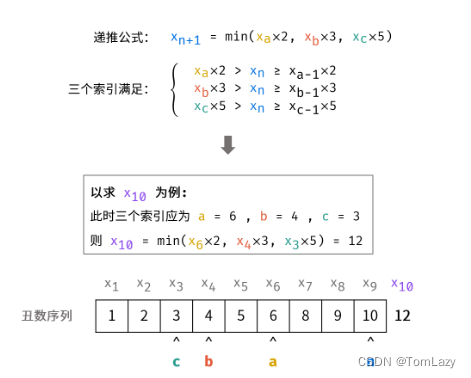
设已知长度为 n 的丑数序列 x1,x2,…,xn，求第 n +1 个丑数 xn+1。根根据递推性质，丑数 xn+1 只可能是以下三种情况其中之一 (索引 a,b,c 为未知数) :

即，要么是乘 2 得到的，要么就是乘 3 得到的，否则就是乘 5 得到的
……
递推公式：

通过递归公式，不断往上递推下一个丑数值，并每次选出可能的最小值存入，间接的相当于进行了排序。
……
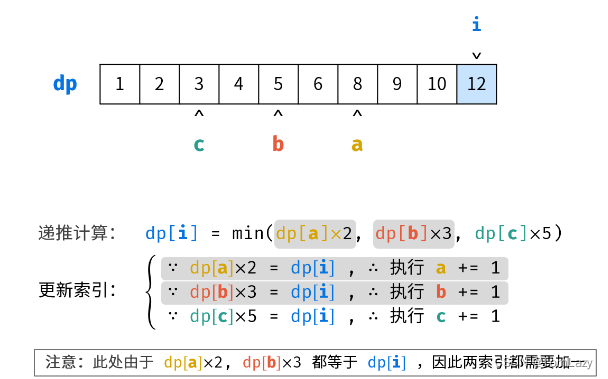
通过定义三个变量作为索引，表示指示递推丑数的下一个可能值（3选1，在里面选最小）：
……
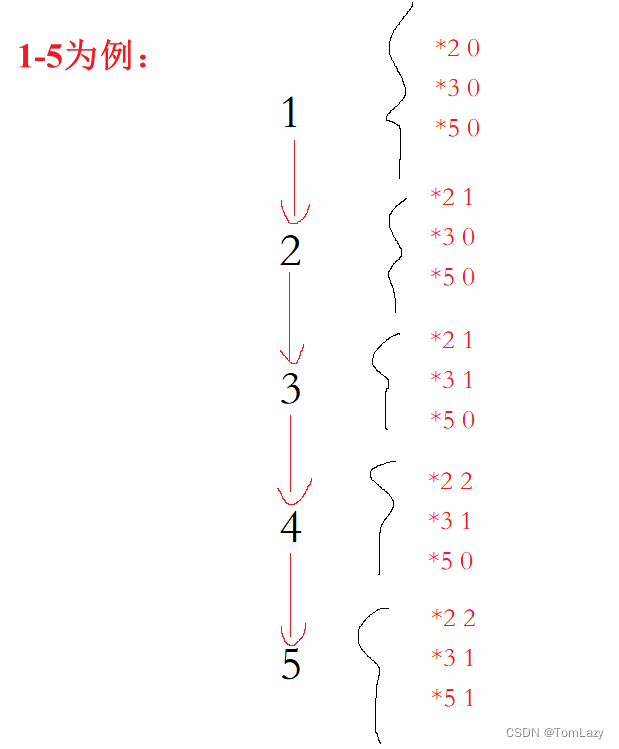
索引变化规律：

class Solution {
    // Solution2：动态规划
    public int nthUglyNumber(int n) {
        // 无效输入判断
        if (n <= 0) return 0;
        // 初始化丑数数组
        int[] ugly = new int[n];
        ugly[0] = 1;
        // 定义三个指针，表示下一个丑数是该指针指向的丑数*2、*3或*5得到的
        int i2 = 0, i3 = 0, i5 = 0;
        // 循环计算丑数
        for (int i = 1; i < n; i++) {
            // 计算下一个丑数
            ugly[i] = Math.min(ugly[i2] * 2, Math.min(ugly[i3] * 3, ugly[i5] * 5));
            // 更新指针
            if (ugly[i] == ugly[i2] * 2) i2++;
            if (ugly[i] == ugly[i3] * 3) i3++;
            if (ugly[i] == ugly[i5] * 5) i5++;
        }
        return ugly[n - 1];
    }
}

3. 参考资料

[1] 剑指 Offer 49. 丑数（动态规划，清晰图解）