当前位置：首页 > article >正文

【LeetCode: 剑指 Offer II 112. 最长递增路径 | 递归 | DFS | 深度优先遍历 | 记忆化缓存表】

article 2024/11/10 7:39:23

在这里插入图片描述

🍎作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🍎座右铭：人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯🎯

在这里插入图片描述

题目链接

剑指 Offer II 112. 最长递增路径
329. 矩阵中的最长递增路径

题目描述

给定一个 m x n 整数矩阵 matrix ，找出其中最长递增路径的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。不能在对角线方向上移动或移动到边界外（即不允许环绕）。

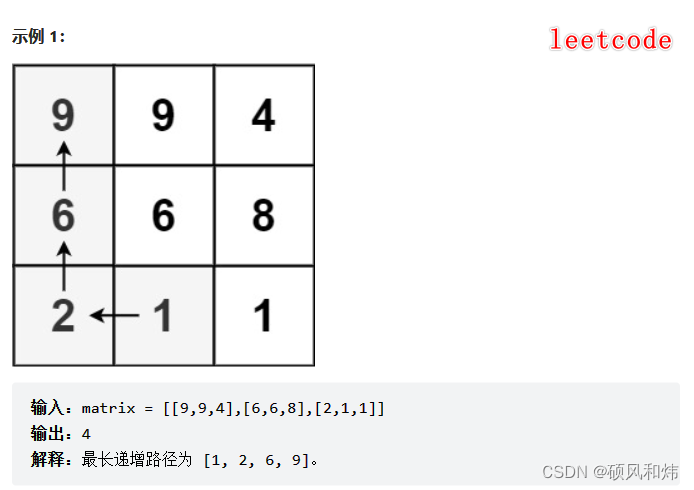
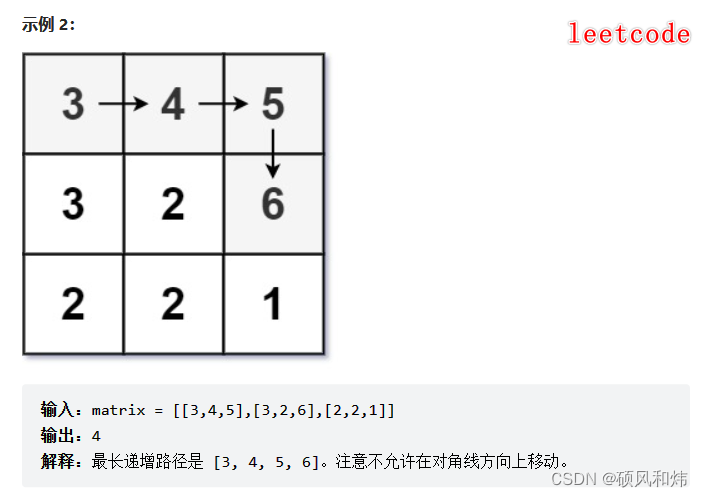
在这里插入图片描述

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1

求解思路&实现代码&运行结果

DFS

求解思路

该题目的求解思路比较简单，我们直接从给定数组中的每一个位置开始遍历，通过DFS的思想找到上、下、左、右中最长的递增路径，记录当前位置的最大长度。
因为我们遍历的是整个数组，从每一个位置开始，所以说我们最后还需要比较每一个位置的长度，找到最长的即可。

实现代码

实现代码的方式有很多，你可以在设计递归的时候将参数放到函数中，也可以将参数设置为成员变量都是可以的，甚至再求一些值的时候，你可以将最后的答案放到参数中，当然也可以将每一步的答案都进行返回，递归设置相应的返回值。方式有很多，大家选择自己最喜欢，最熟悉的方式即可。

class Solution {
    public int longestIncreasingPath(int[][] matrix) {
        int m=matrix.length,n=matrix[0].length;
        int max=Integer.MIN_VALUE;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                max=Math.max(max,process(i,j,m,n,matrix));
            }
        }
        return max;
    }

    public int process(int x,int y,int m,int n,int[][] matrix){
        int up=x>0&&matrix[x][y]<matrix[x-1][y]?process(x-1,y,m,n,matrix):0;
        int right=y<n-1&&matrix[x][y]<matrix[x][y+1]?process(x,y+1,m,n,matrix):0;
        int down=x<m-1&&matrix[x][y]<matrix[x+1][y]?process(x+1,y,m,n,matrix):0;
        int left=y>0&&matrix[x][y]<matrix[x][y-1]?process(x,y-1,m,n,matrix):0;
        return Math.max(Math.max(up,right),Math.max(down,left))+1;
    }
}

运行结果

我们可以看到时间超限了，不要紧，至少证明我们的思路是没有问题的，我们可以继续优化嘛。
在这里插入图片描述

记忆化缓存

求解思路

我们直接添加一个缓存表，避免一个结果会重复产生计算，如果我们之前计算过，此时直接返回就可以。

实现代码

class Solution {
    public int longestIncreasingPath(int[][] matrix) {
        int m=matrix.length,n=matrix[0].length;
        int[][] dp=new int[m][n];
        for(int i=0;i<m;i++){
            Arrays.fill(dp[i],-1);
        }
        int max=Integer.MIN_VALUE;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                max=Math.max(max,process(i,j,m,n,matrix,dp));
            }
        }
        return max;
    }

    public int process(int x,int y,int m,int n,int[][] matrix,int[][] dp){
        if(dp[x][y]!=-1) return dp[x][y];
        int up=x>0&&matrix[x][y]<matrix[x-1][y]?process(x-1,y,m,n,matrix,dp):0;
        int right=y<n-1&&matrix[x][y]<matrix[x][y+1]?process(x,y+1,m,n,matrix,dp):0;
        int down=x<m-1&&matrix[x][y]<matrix[x+1][y]?process(x+1,y,m,n,matrix,dp):0;
        int left=y>0&&matrix[x][y]<matrix[x][y-1]?process(x,y-1,m,n,matrix,dp):0;
        return dp[x][y]=Math.max(Math.max(up,right),Math.max(down,left))+1;
    }
}