编译原理期末速成笔记
哈喽大家好,又要考试了,在这里分享一下我的两天速成笔记,参考视频为哔站 Deeplei_ 的《编译原理期末速成》。本文仅是知识点总结,至于考试内容待我研究一下,后续我会再发文对考试的各个模块做详细分析,欢迎评论区留言!
目录
1. 求表达式的四元式
2. 求表达式的逆波兰式
3. 根据文法写出语言
4. 分析句型构造语法树
5. 求短语、直接短语和句柄
6. 正规式转正规文法
7. 正规文法转正规式
8. 正规式转 NFA
9. NFA 确定化及 DFA 最小化
10. 消除左公因子和左递归
11. 求 First 集、Follow 集和 Select 集
12. 构造 LL(1) 预测分析表
13.构造 LR(0) 项目集规范族
14. 构造 LR(0) 和 SLR(1) 分析表
1. 求表达式的四元式
四元式格式:(运算符,运算对象1,运算对象2,临时变量)
规则:
① 先处理优先级高的一部分,然后向左遍历;
② 每一次运算结果用一个变量接收,以便后续使用。
写出 a + b * ( c / d + g ) 的四元表达式。
(/,c,d,t1)
(+,t1,g,t2)
(*,b,t2,t3)
(+,a,t3,t4)
2. 求表达式的逆波兰式
先在草稿上画一个栈,读取符号时进栈,出栈时出栈的符号追加到答案后面,读取完毕后栈中的符号要依次出栈。
规则:
① 从左到右读取表达式;
② 遇到字母直接写到答案中;
③ 遇到符号,加入栈中;
④ 遇到成对括号,才出栈;
⑤ 新加入的符号优先级要高于原栈顶优先级,否则栈中符号先出栈。
写出 a + b * ( c / d + g ) 的逆波兰式。
逆波兰式:abcd/g+*+
3. 根据文法写出语言
句子是句型的特殊情况,句子的集合叫语言。
① N → D|ND
② D → 0|1|2|3|4|5|6|7|8|9
问 G[N] 的语言是什么?

4. 分析句型构造语法树
根据推到过程按顺序画出语法树。
令文法 G[E] 为:
E → E + T|T
T → T * F|F
F → (E)|v|d
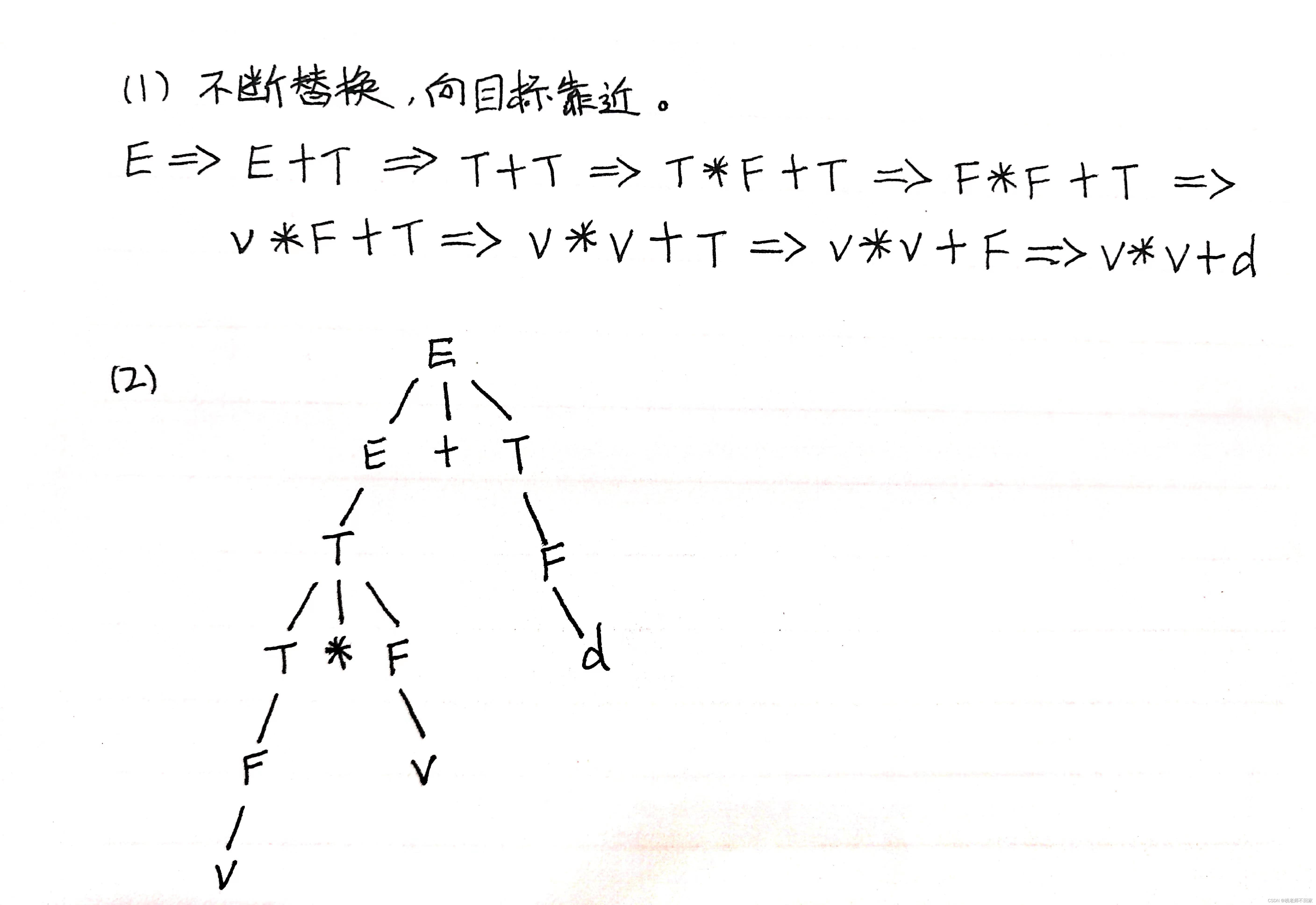
(1)分析说明 v * v + d 是它的一个句型。
(2)画出上一问的语法树。
5. 求短语、直接短语和句柄
还是以上面的题为例,根据画出的语法树求短语、直接短语和句柄。
求短语,找出所有的父节点,从最后一层开始往上看,把父节点的叶子进行组合,在同一层上从左到右看,同一个叶子不用重复写。
短语:v,v,v * v,d,v * v + d 。
直接短语是短语的特殊情况,首先找出只有一层的简单子树,一个父节点加上它的子节点,该子节点以下再无结点,一般都在末层去找,简单子树的短语就是直接短语。
直接短语:v,v,d 。
写出的直接短语中最左边的那个短语就叫句柄。
句柄:v 。
6. 正规式转正规文法
套用公式进行改写:
① 已知 A → x|y,改写为 A → x,A → y;
② 已知 A → xy,改写为 A → xB,B → y;
③ 已知 A → x*y,改写为 A → xB,A → y,B → xB,B → y。
将正规式 r = a(a|d)* 转换为相应的正规文法 G[S]。
设开始符号为 S,则 S → a(a|d)*

7. 正规文法转正规式
公式实际上就是正规式转正规文法逆过来:
① 已知 A → x,A → y,推出正规式 A = x|y;
② 已知 A → xB,B → y,推出正规式 A = xy;
③ 已知 A → xA|y,推出正规式 A = x*y。
文法G[S]:
S → aA
S → a
A → aA
A → dA
A → a
A → d
将以上文法转为正规式。
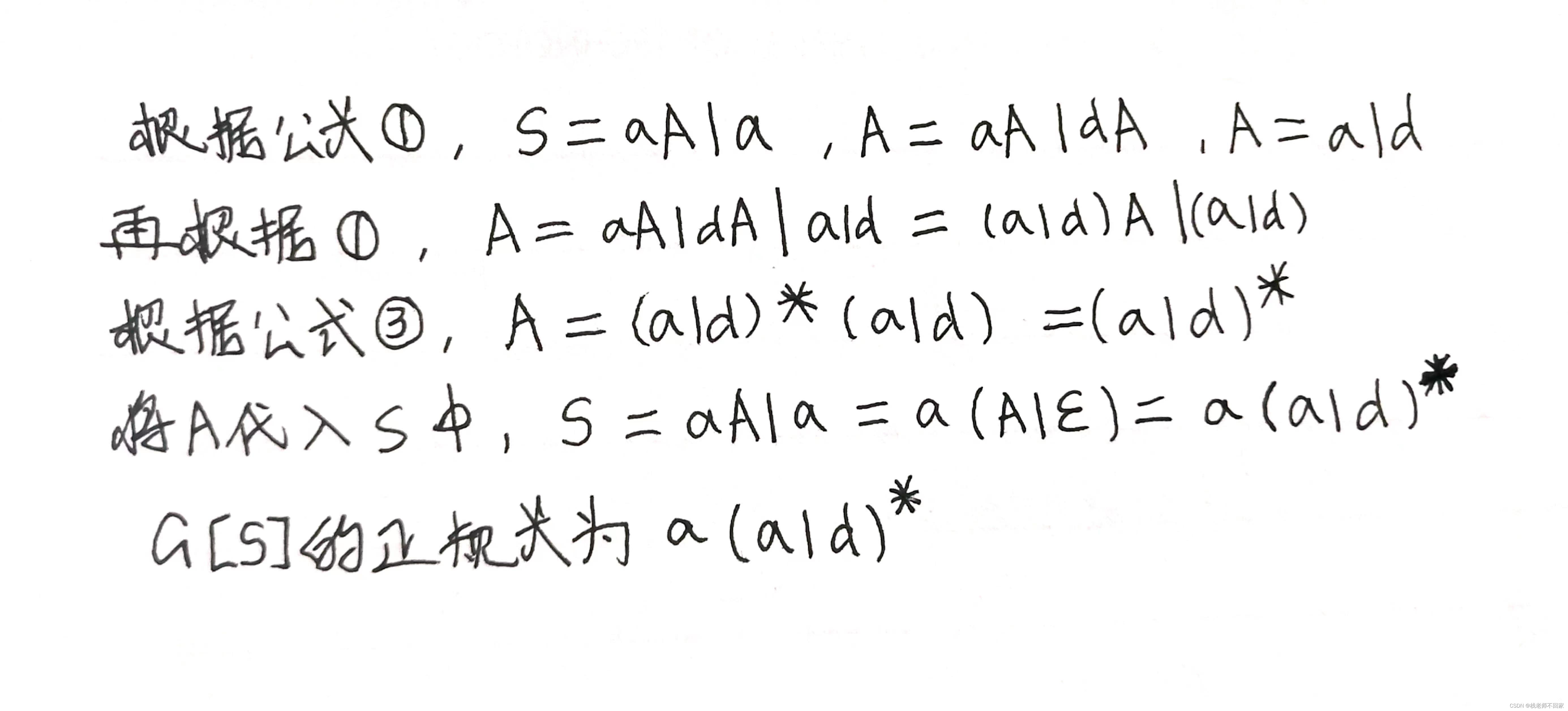
8. 正规式转 NFA
先从外往里看,里面暂时看成整体,根据以下规则画出 NFA。
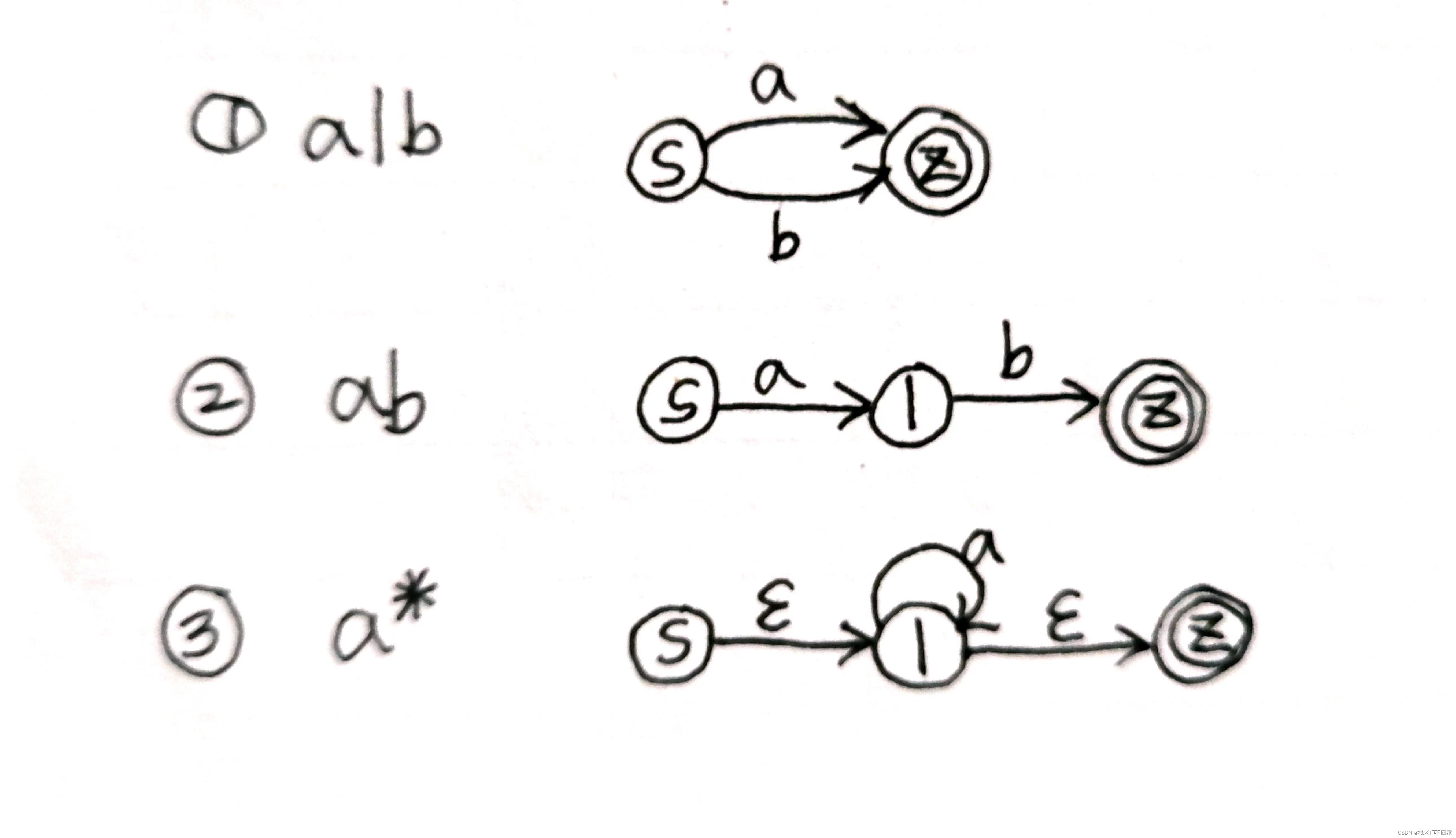
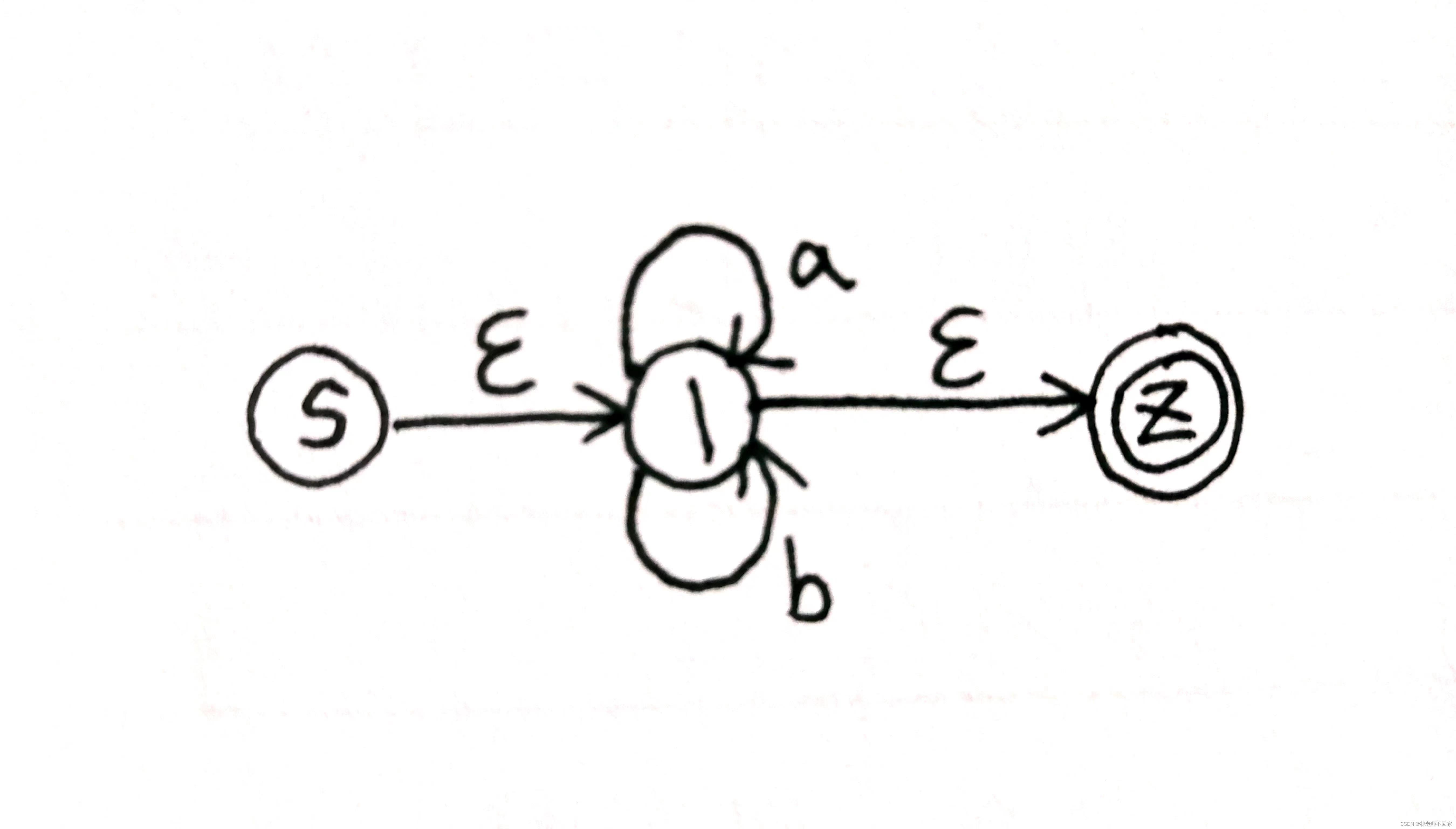
正规式 (a|b)* 的NFA如下:
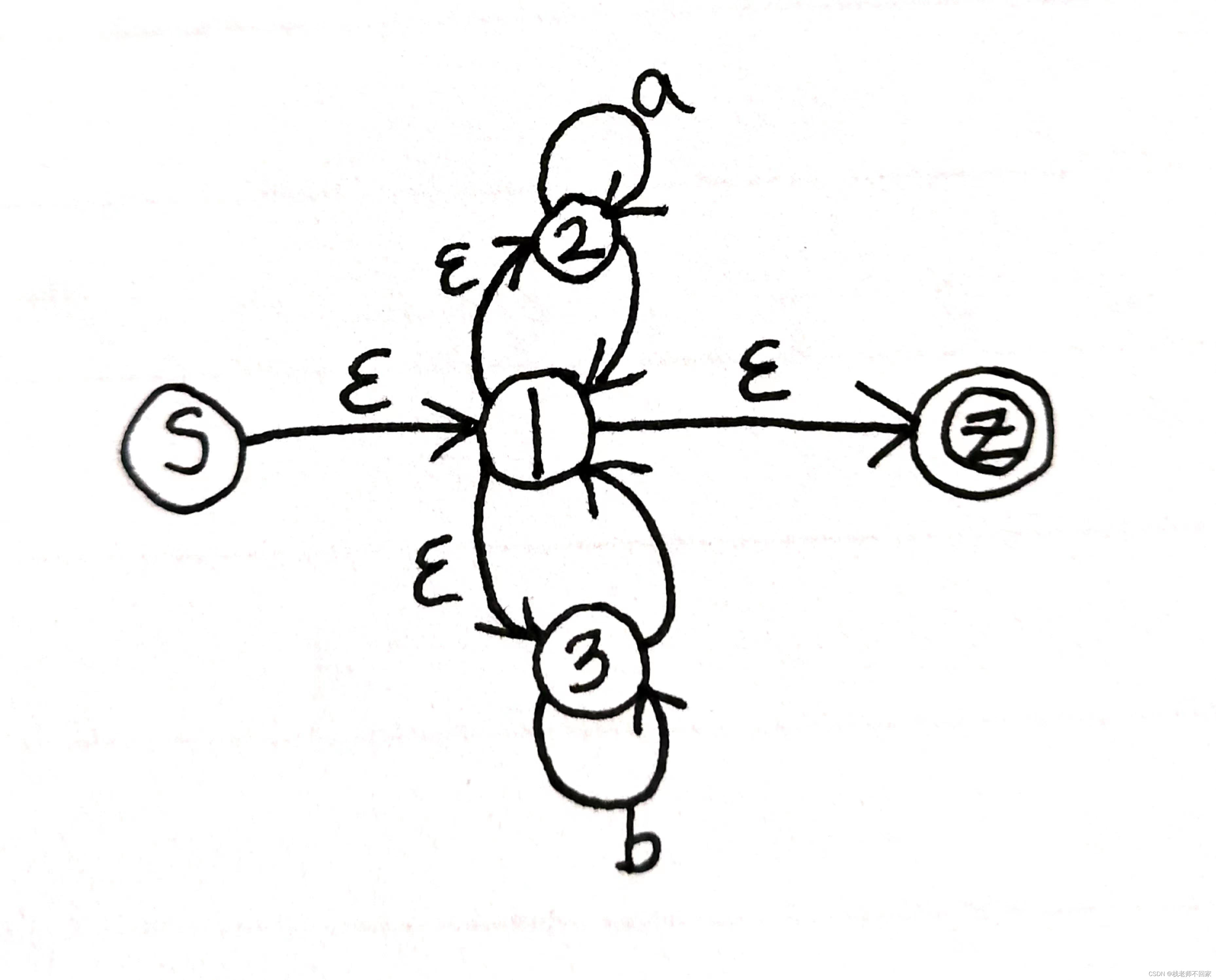
正规式 (a*|b*)* 的NFA如下:
9. NFA 确定化及 DFA 最小化
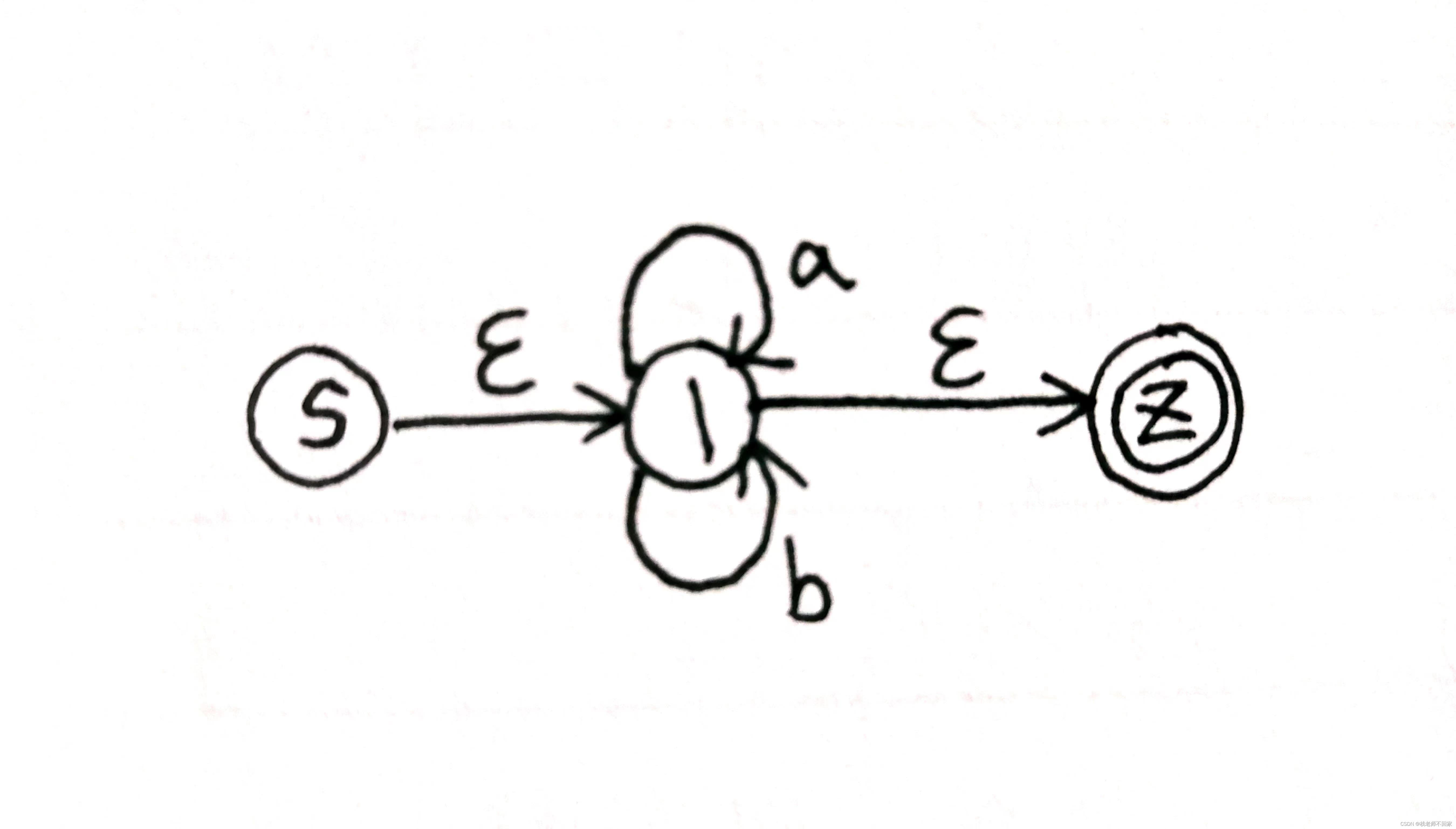
以正规式 (a|b)* 为例,其 NFA 如下:
NFA的确定化即 DFA:

DFA 最小化:
含有终态状态的集合称为终态集,除此之外都是初态集,本例中的终态状态为 Z。

10. 消除左公因子和左递归
规则如下:

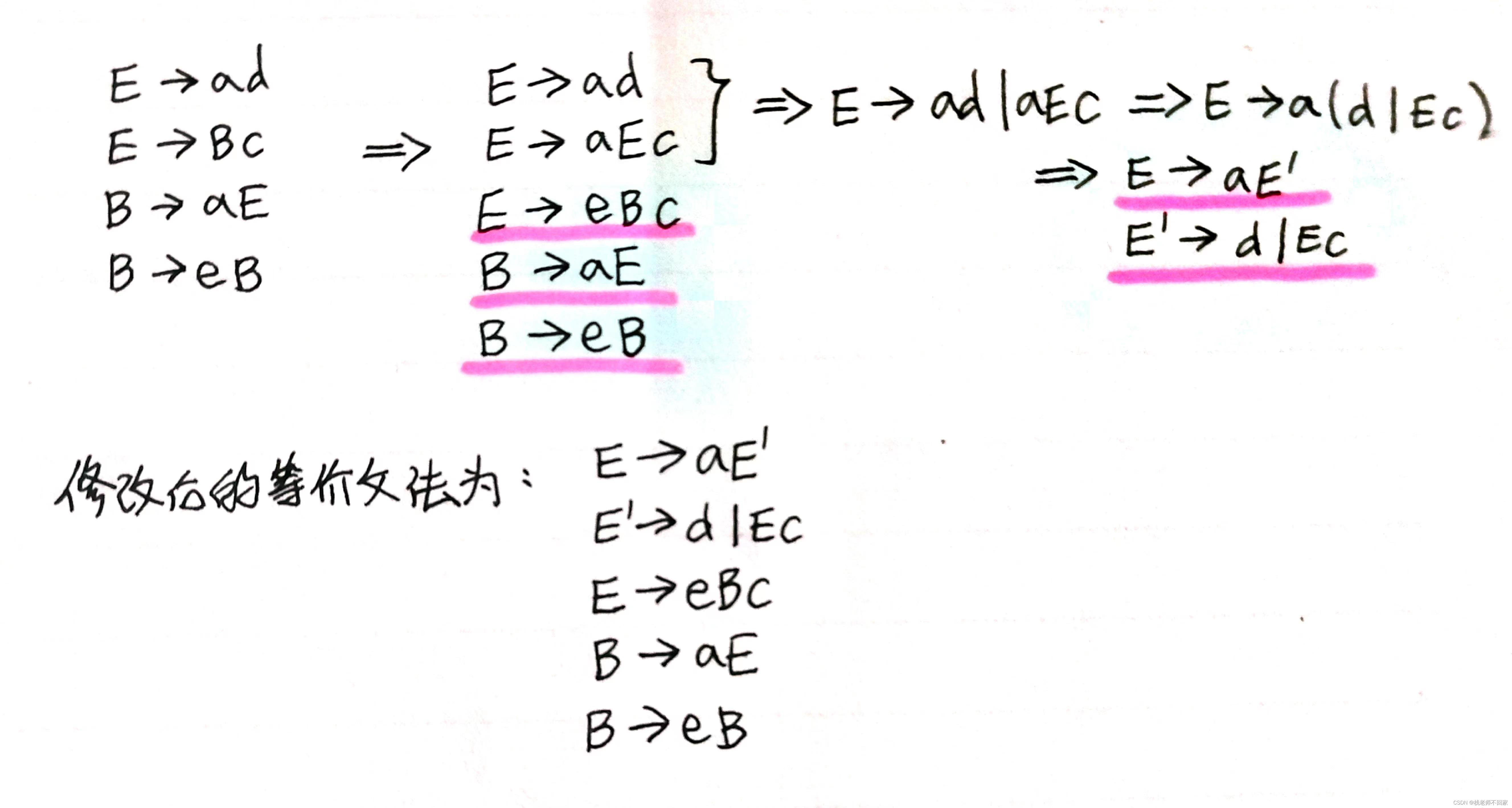
已知文法 G[E]:
E → ad | Bc
B → aE | eB
提取左公共因子,给出修改后的等价文法。
11. 求 First 集、Follow 集和 Select 集
求 First 集规则如下:
(1)A → aB(A → ab),First(A) = {a}
(2)A → aB | 空串,First(A) = {a, 空串}
(3)A → BCD,First(A) = {First(B)}
(4)A → BCD,B → 空串,First(A) = {First(B), First(C)}
(5)A → BCD,B → 空串,C → 空串,First(A) = {First(B), First(C), First(D)}
(6)终结符的 First 集就是它本身,First(a) = {a}
求 Follow 集规则如下:
(1)若要求的是开始符号的 Follow 集,则集合中必有 #,Follow(S) = {#, ...}
(2)A → aBb,Follow(B) = {First(b)} - 空串
(3)A → aB,Follow(B) = {Follow(A)}
求 Select 集规则如下:
(1)若 a 可经过 n 步推出空串,则 Select(A → a) = [First(a) - 空串] U Follow(A)
(2)若 a 不是空串,则 Select(A → a) = First(a)
还以上一题为例:

当左部相同的产生式的 Select 集的交集都是空集时,就可证明该文法是 LL(1) 文法。
12. 构造 LL(1) 预测分析表
构造过程:
① 横向表头处沿 x 轴方向,按给出的右部文法顺序,依次填入终结符,包括 #;
② 纵向表头处沿 y 轴方向,按给出的左部文法顺序,依次填入非终结符;
③ 表格内容填入产生式,所在表格的横坐标为该产生式的左部,所在表格的纵坐标是该产生式 Select 集的一个元素;
④ 构造表格时先把 Select 集全写出来;
⑤ 不满足填入产生式的条件时,就什么都不用填。
依然接着上面的例子:

13.构造 LR(0) 项目集规范族
项目的概念:
① 右部标有小圆点的产生式称为一个项目;
② 若小圆点后面是一个终结符,它就被称为移进项目;
③ 若小圆点后面是一个非终结符,它就被称为待约项目;
④ 若小圆点放在了最后面,则称该项目为归约项目。
增广文法的概念用文字不好描述,我们直接看例子:


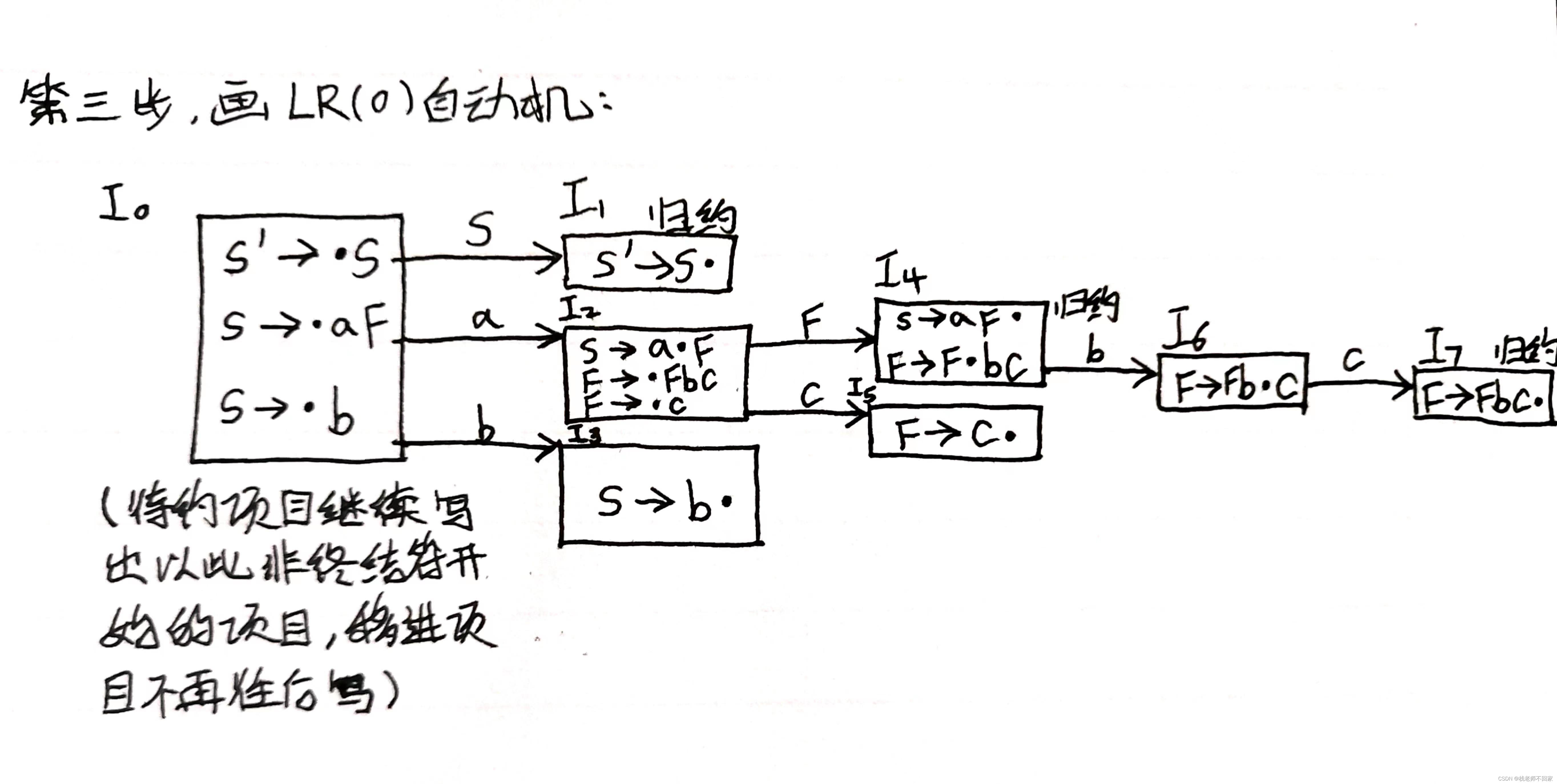

把 LR(0) 自动机方框中的内容分别写到项目集合中就是规范族。
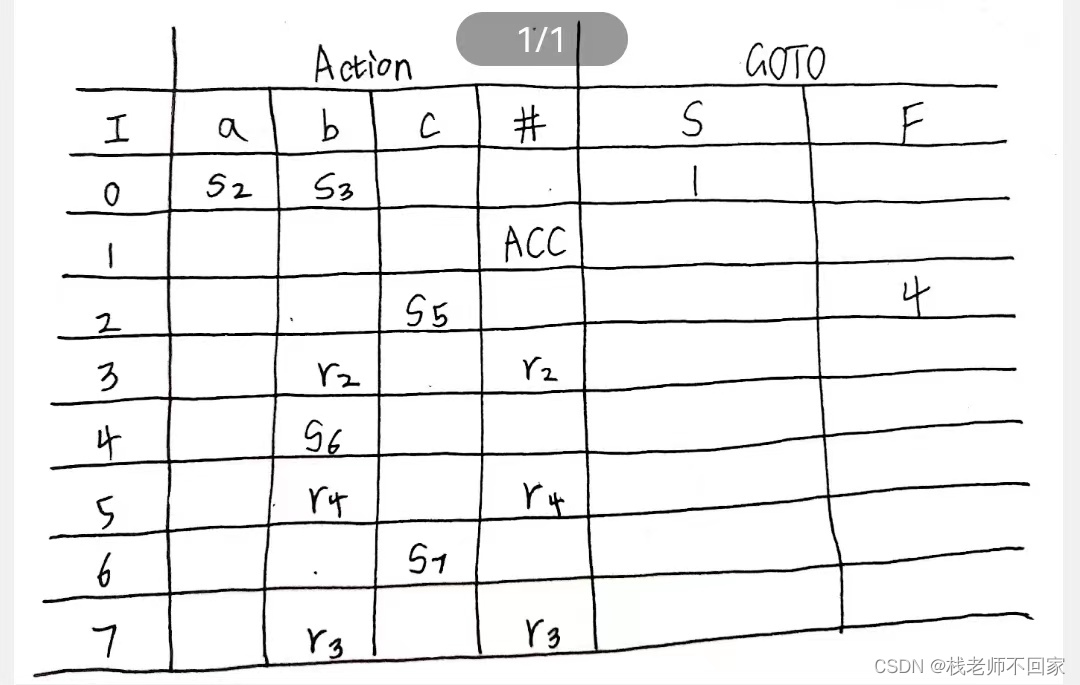
14. 构造 LR(0) 和 SLR(1) 分析表
分析表的结构:
① Action 栏表头填终结符和 # 号,GOTO 栏表头填入非终结符,不包括增广文法时引入的 S’;
② 表格内容,根据上问的自动机图,比如第一行,I0 通过 a 到达 I2,由于 a 是终结符,Action 栏统一写为 S 加序号,所以为 S2,对于 GOTO 栏直接写序号即可,I0 通过 S 到达 I1,所以这里填 1,后面同理;
③ 对于归约项目有I1、I3、I5、I7,其中 I1 的 # 位置统一写 ACC,对于 I3、I5 和 I7 道理一样,这里以 I3 为例,首先去自动机图里找到 I3 所对应的框框,里面是 S → b,然后去上面增广文法的展开式中找 S → b,得到它的索引序号为 2,那么 I3 所对应的 Action 列暂时全部写上 r2;
④ I4 处出现移入和归约冲突的问题,这时就需要通过 Follow 集来进行判断,Follow(S) = {#},Follow(F) = {b,#},b 不属于Follow(S),属于 Follow(F),所以 I4 这里选择移入;
⑤ 修改 I3、I5 和 I7 行,除了 Follow 集中的终结符 b 列外,a 和 c 列均不采用归约,也就是说把 a、c 列的值去掉。