2018年五一杯数学建模C题江苏省本科教育质量综合评价解题全过程文档及程序
2019年五一杯数学建模
C题 江苏省本科教育质量综合评价
原题再现
随着中国的改革开放,国家的综合实力不断增强,中国高等教育发展整体已进入世界中上水平。作为一个教育大省,江苏省的本科教育发展在全国名列前茅,而江苏省13个地级市的本科教育质量发展并不平衡。
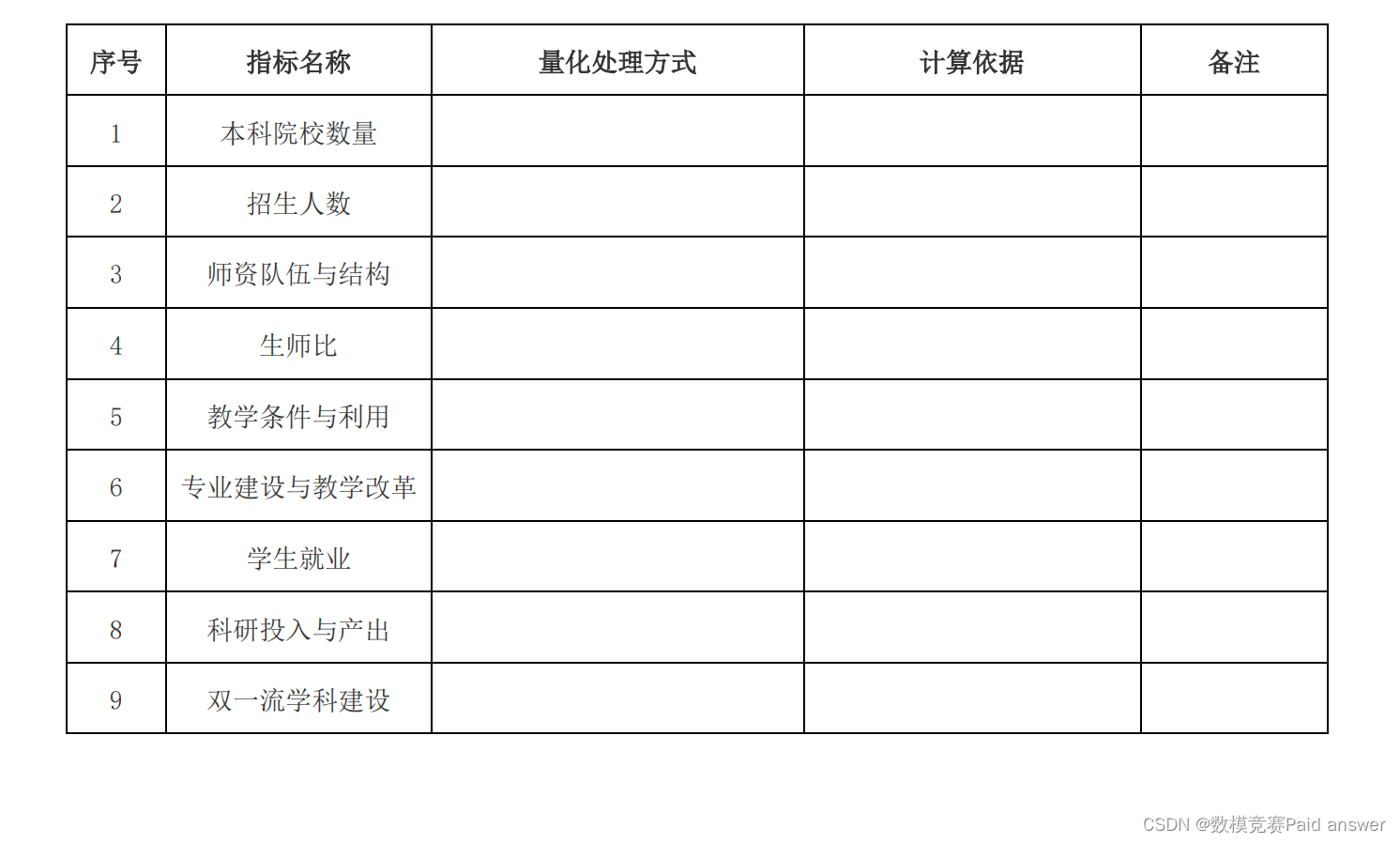
1. 影响本科教育质量的指标有很多。查找资料,对如下9个指标(本科院校数量、招生人数、师资队伍与结构、生师比、教学条件与利用、专业建设与教学改革、学生就业、科研投入与产出、双一流学科建设)进行量化处理(完成下表),并进行相关的数据分析。
2. 根据问题1中的指标数据,建立数学模型,对江苏省13个地级市(常州、淮安、连云港、南京、南通、宿迁、苏州、泰州、无锡、徐州、盐城、扬州、镇江)的本科教育质量进行综合评价。
3. 通过建立数学模型,分析在所给的9个指标中,可以减少哪些指标使得评价结果与问题2中的评价结果基本一致。
4. 通过建立数学模型,确定一个关键的指标,使得该指标值的普遍改善能够尽可能缩小江苏省13个地级市本科教育发展的差异,并利用查找的数据资料验证所建立模型的有效性。
5. 请结合前面的讨论给出有效提升江苏省本科教育质量的政策建议。
整体求解过程概述(摘要)
本文运用熵权法、主成分分析法、虚拟控制调节法、灰色关联分析等方法,建立了江苏省 13 个地级市本科教育质量的综合评价模型,并对该模型中的指标进一步优化与筛选,对江苏省的本科教育质量问题进行了研究。
问题一中,本文基于给定的九个指标,参考现存的多种评价体系与原则,综合考虑分析后完成一套完备的四级指标评价体系,并基于熵权法构建评估本科教育质量的综合评价模型,对给定的九个指标进行了合理的量化。
问题二中,本文综合考虑指标的客观与主观因素,利用熵权法和主成分分析法互为验证,得到更有效的综合评价模型。基于问题一各三级指标的量化值,进行无量纲化处理。根据处理后的无量纲值,先利用主成分分析,确定各成分的信息贡献率和累积贡献率,利用其信息贡献率得到江苏省 13 个城市本科质量的综合评价模型。本文再利用熵权法,对模型中各指标的权重进行求解赋值,并建立最终的江苏省 13 个地级市本科教育质量的综合评价模型。对于两种不同的模型,本文分别计算得到 13 个城市的本科质量综合得分,得到基于这两个模型的江苏省 13 个地级市的本科教育质量排名。对比分析两种模型得到的排名,最后得到的结果为:南京>苏州>无锡>南通>镇江>徐州>扬州>盐城>淮安>常州>连云港市>泰州>宿迁。
问题三中,引入虚拟控制城市,通过控制 13 个城市三级指标数据进行相同幅度的调节,计算调节前后 13 个城市的本科教育质量综合评分间的相对欧式距离。本文利用灰色关联分析,验证这一方法的可靠,得到各三级指标与本科教育质量的关联度。本科院校数量、招生人数这两项指标的相对欧氏距离与关联度均较小,说明这两项指标对本科教育质量的影响较小。减少这两项指标后再带入建立的综合评价模型的排名变化浮动较小,因此可以减少本科院校数量、招生人数这两项三级指标。
问题四中,利用敏感度分析,选择其余 7 个指标为主要三级指标,每次仅改变一个指标,与其他未改变的组成一个新指标集,重新计算其综合得分,得到敏感度。将敏感度最大的专业建设与改革作为关键指标,比较仅改变该值与未改变该值的江苏省 13 个地级市本科教育质量的得分,发现各市评分差距均明显降低,且得分越低的城市的增长量明显越高,该指标确实可以缩小江苏省 13 个地级市本科教育发展的差异。
问题五中,根据前四问的综合评价模型分析出江苏省各地级市本科教育质量不均衡的原因,并针对现实情况,结合当下政策,提出了合理有效的建议。
模型假设:
1.假设网上搜集的数据真实可靠,不存在异常数据。
2.假设各高校自然发展,没有特殊情况导致其综合实力剧变。
3. 假设不考虑民办与中外合办本科院校时,不影响教育综合质量的评价。
4. 假设对某些指标采取的调整措施不会影响其他指标。
问题分析:
江苏省位于长江三角洲经济发达地区,综合实力强劲,高等教育资源优渥,但仍然存在着教育发展不平衡的现象,省内十三个地级市的高等教育资源分配差异较为显著。对江苏省本科教育质量进行综合评估,可以体现出江苏省高等教育所存在的缺陷与问题,利于教育改革的推进和各高校的健康发展。因此,进行江苏省本科教育质量综合评估具有十分重要的意义。
关于问题一的分析
问题一要求对给出的九个指标进行量化处理,并进行相关的数据分析。由于江苏省本科教育质量受多种复杂因素作用的影响, 且在选取评价指标时需要考虑到指标的可行性、 指标选取的主观性等因素的影响, 因此可以基于熵权法进行客观赋权,建立一个多层次的江苏省本科教育质量评价指标体系。
关于问题二的分析
问题二要求对问题一中的指标数据,建立数学模型,对江苏省 13 个地级市的本科教育质量进行综合评价。考虑到指标针对这十三个地级市的可行性, 将收集到的数据标准化后用熵权法计算各指标权重, 最后代入第一问的评价体系即可求出综合评分进行排名。
关于问题三的分析
问题三要求在所给的九个指标中,可以减少那些指标使评价结果与问题二中的评价结果基本一致。可以考虑根据分析各项指标的灵敏性来判断指标对目标层影响的大小。为了能更直观地调控各指标的变量, 且使各变量值对该指标的影响是等效的, 本文考虑插入一个虚拟控制变量。 通过调节改虚拟控制变量的各指标数据,计算各指标的灵敏度,从而确定出各指标变化对目标层的影响效果。
关于问题四的分析
问题四要求确定一个关键的指标,使得该指标值得普遍该晒能够尽可能缩小江苏省 13 个地级市本科教育发展差异。可以考虑敏感度分析,任意改变主要三级指标的综合得分,对比改变前后 13 个地级市本科教学质量的得分,来判断该关键指标是否符合要求。
关于问题五的分析
问题五要求我们结合前面的讨论,给出有效提升江苏省本科教育质量的政策建议。考虑根据问题一至问题四中获得的所有可能结果进行多方面地分析,采取重点对策来提出了对有效提升江苏省本科教育质量的科学且有依据的政策建议。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
clc
A=[1 5
1/5 1];
n=2;
e0=ones(n,1);
e0=(1/n)*e0;
for i=1:n
e0=A*e0;
e=e0/sum(e0);
e1=zeros(n,1);
e1=e;
if e0==e1
break
end
end
e1
clc
n=5;
x=zeros(n,n);
Aa=zeros(n,n);
ans0=0;
A=[ 1 2 7 5 5
1/2 1 4 3 3
1/7 1/4 1 1/2 1/3
1/5 1/3 2 1 1
1/5 1/3 3 1 1];
w=sum(A);
for i=1:25
if (i<=5)
Aa(i)=A(i)/w(1);
else if (i<=10)
Aa(i)=A(i)/w(2);
else if (i<=15)
Aa(i)=A(i)/w(3);
else if (i<=20)
Aa(i)=A(i)/w(4);
else
Aa(i)=A(i)/w(5);
end
end
B=sum(Aa');
k=sum(B);
for i=1:n
B(i)=(B(i))/k
end
w=B'
aw=A*w;
for i=1:n
ans0=ans0+(1/n)*(aw(i)/w(i));
end
ans0
CI=(ans0-n)/(n-1)
CR=CI/1.12
clc
A=[1 1/3 1/3
3 1 5
3 1/5 1];
n=3;
e0=ones(n,1);
e0=(1/n)*e0;
for i=1:n
e0=A*e0;
e=e0/sum(e0)
e1=zeros(n,1);
e1=e;
if e0==e1
break
end
end
e1
clc,clear
x=[3 39152 8341 16.6 100 550653 0 0.9288
2 21410 0 18.7 50 339561 0 0.9079
2 11545 0 18.16 70 91484 0 0.8905
35 329483 0 20.4 55 1429259 38 0.9134
3 31641 7327 19.21 75 992409 0 0.9212
1 47960 2 21.8 35 359100 0 0.8724
7 67413 018.7 90 1193750 1 0.9242
5 19226 0 18.9 40 1350277 0 0.9023
2 34462 0 18.5 80 429389 2 0.9243
6 53992 12098 17.1 95 964210 2 0.876
2 18334 4399 15.8 65 557704 0 0.9167
3 22405 0 15.8 85 790380 0 0.9262
2 25760 10162 15.4 60 1077366 0 0.8642
];
x=zscore(x); %数据标准化
std=CORRCOEF(x); %计算相关系数矩阵
[vec,val]=eig(std); %求特征值(val)及特征向量(vec)
newval=diag(val); %将特征值做成一个新向量
[y,i]=sort(newval); %对特征值进行排序,y为排序结果,i为索引
rate=y/sum(y) %计算贡献率
sumrate=0;
newi=[];
for k=length(y);-1;1
sumrate=sumrate+rate(k);
newi(length(y)+1-k)=i(k);
if sumrate>0.85 break;
end
end %记下累积贡献率大于85%的特征值的序号方人员newi中
fprintf('主成分数;%g\n\n',length(newi));
for i=1;1;1;length(newi) %计算荷载aa
for j=1;1;1length(y)
aa(i,j)=sqrt(newval(newi(i)))*vec(j,newi(i));
end
end
aaa=aa.*aa; %主成分荷载归一化zcfhz
for i=1;1;length(newi)
for j=1;1;length(y)
zcfhz(i,j)=aa(i,j)/sqrt(sun(aaa(i,;)));
end
end
fprintf('主成分荷载;/n'),zcfhz %输出主成分荷载zcfhz
