当前位置：首页 > article >正文

数据结构与算法（四）分治算法（Java）

article 2024/11/14 12:13:51

一、简介

1.1 背景

在学习分治算法之前，我们先来举一个例子。

假如你有一个存钱罐，过年家人给的钱都会放到存钱罐中。当我们想要清点存钱罐中的钱时，一堆钱混乱的放在一起很难清点，并且容易算错。那我们可以这样，先将存钱罐中的钱分成几小份，然后再求和就可以了。

在这里插入图片描述

如果我们还是觉得各个部分的钱数太大，依然可以进行划分然后合并，比如每凑够100元为一组等。梳理下思路，我们之所以这么做是因为以下两点：

划分后的子问题更易求解；
父问题的结果可以直接由子问题的结果计算得到。

其实这就是一种分治的思想。

1.2 定义

分治算法：是一种 将一个问题分解为多个子问题，分别求解这些子问题 的解决方法，主要用于递归计算中。

1.3 步骤

具体来说，分治算法通常包括三个步骤：

分解原问题为若干子问题；
解决这些子问题，递归地运用分治算法；
合并这些子问题的解为一个整体。

1.4 时间复杂度

分治算法的时间复杂度通常为 O(nlogn)。

二、经典示例

分治算法的经典使用示例包括：

二分搜索
快速排序
归并排序
最大子序列和
其他：最近点对、大整数乘法、Strassen矩阵乘法、棋盘覆盖、线性时间选择、循环赛日程表、汉诺塔等。

2.1 二分搜索

二分查找

二分搜索是分治算法的一个示例，只不过二分搜索有着自己的特殊性：

序列有序；
结果为一个值。

思路：

先将一个完整的区间分成两个区间；
两个区间本应单独找值然后确认结果，但是通过有序的区间可以直接确定结果所在区间，然后对结果所在区间进行再次划分；
直到找到值。

代码实现：

实现方式有递归和非递归两种，但是非递归用得更多一些：

/**
 * 二分查找
 * @param nums 数组
 * @param target 目标值
 * @return 位置
 */
public int binarySearch(int[] nums, int target) {
    // 超出范围
    if (target < nums[0] || target > nums[nums.length - 1]) {
        return -1;
    }
    // 判断边界
    if (target == nums[0]) {
        return 0;
    }
    if (target == nums[nums.length - 1]) {
        return nums.length - 1;
    }
    // 二分查找
    int left = 0, right = nums.length - 1;
    int index = 1;
    while (left < right - 1) {
        System.out.println("查找次数：" + index++);
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (target < nums[mid]) {
            right = mid;
        } else {
            left = mid;
        }
    }
    return -1;
}

2.2 快速排序

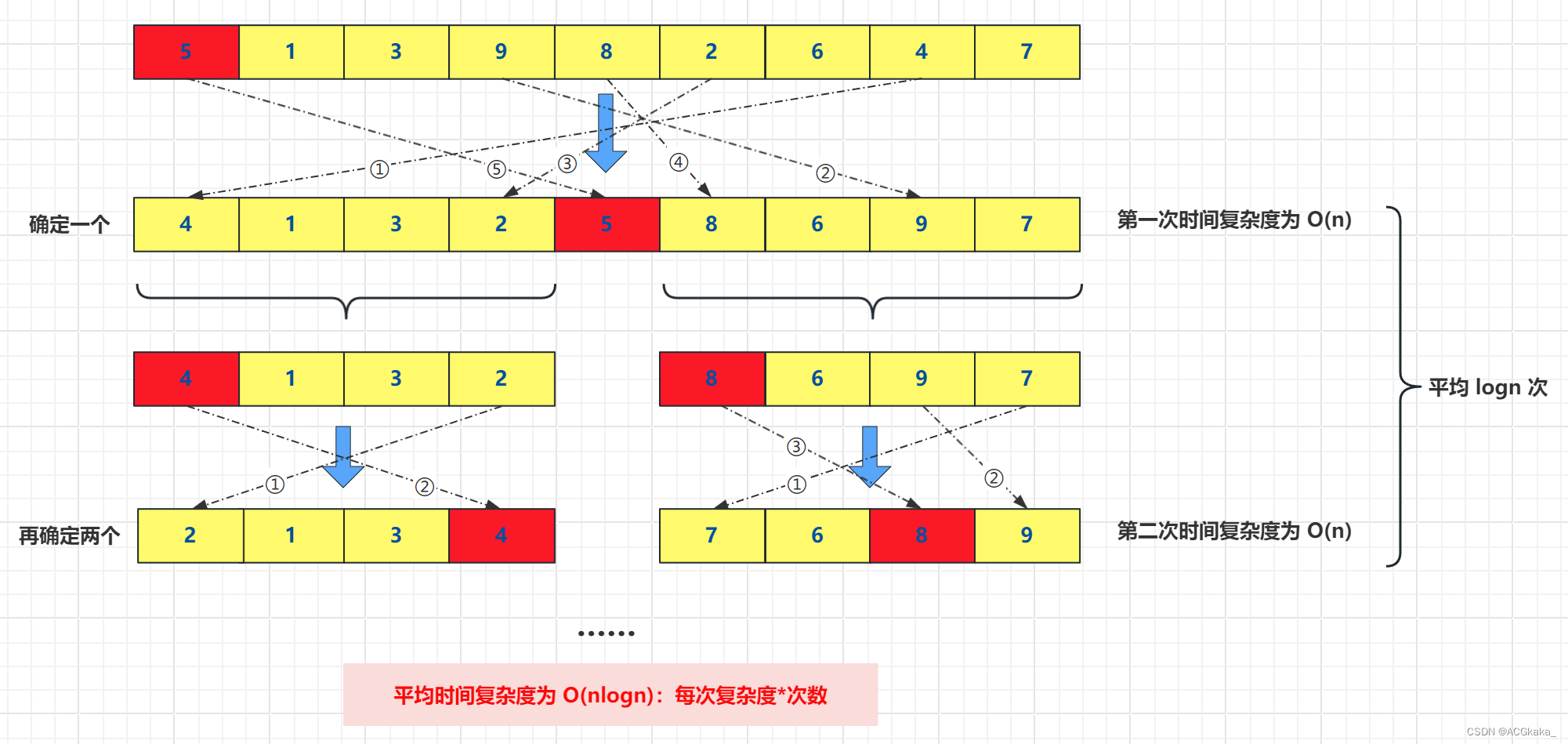
快速排序，简称快排，也是分治算法的一个示例。

思路：

快排每一次遍历会选定一个数，将比这个数小得放左面，比这个数大的放右面；
然后递归分治求解两个子区间；
快排在划分时就做了很多工作，当划分到最底层的时候，最后的序列值就是排序完的值。

快排是一种分而治之的体现。

在这里插入图片描述

代码实现：

public int[] sortArray(int[] nums) {
    quickSort(nums, 0, nums.length - 1);
    return nums;
}
/**
 * 快速排序
 * @param nums  数组
 * @param left  起始位置
 * @param right 结束位置
 */
private void quickSort(int[] nums, int left, int right) {
    if (left > right) {
        return;
    }
    int l = left;
    int r = right;
    // 中心轴
    int pivot = nums[l];
    while (l < r) {
        // 找到第一个小于k的值
        while (nums[r] >= pivot && r > l) {
            r--;
        }
        nums[l] = nums[r];
        // 找到第一个大于k的值
        while (nums[l] <= pivot && l < r) {
            l++;
        }
        nums[r] = nums[l];
    }
    nums[l] = pivot;
    quickSort(nums, left, r - 1);
    quickSort(nums, l + 1, right);
}

2.3 归并排序（逆序数）

排序数组

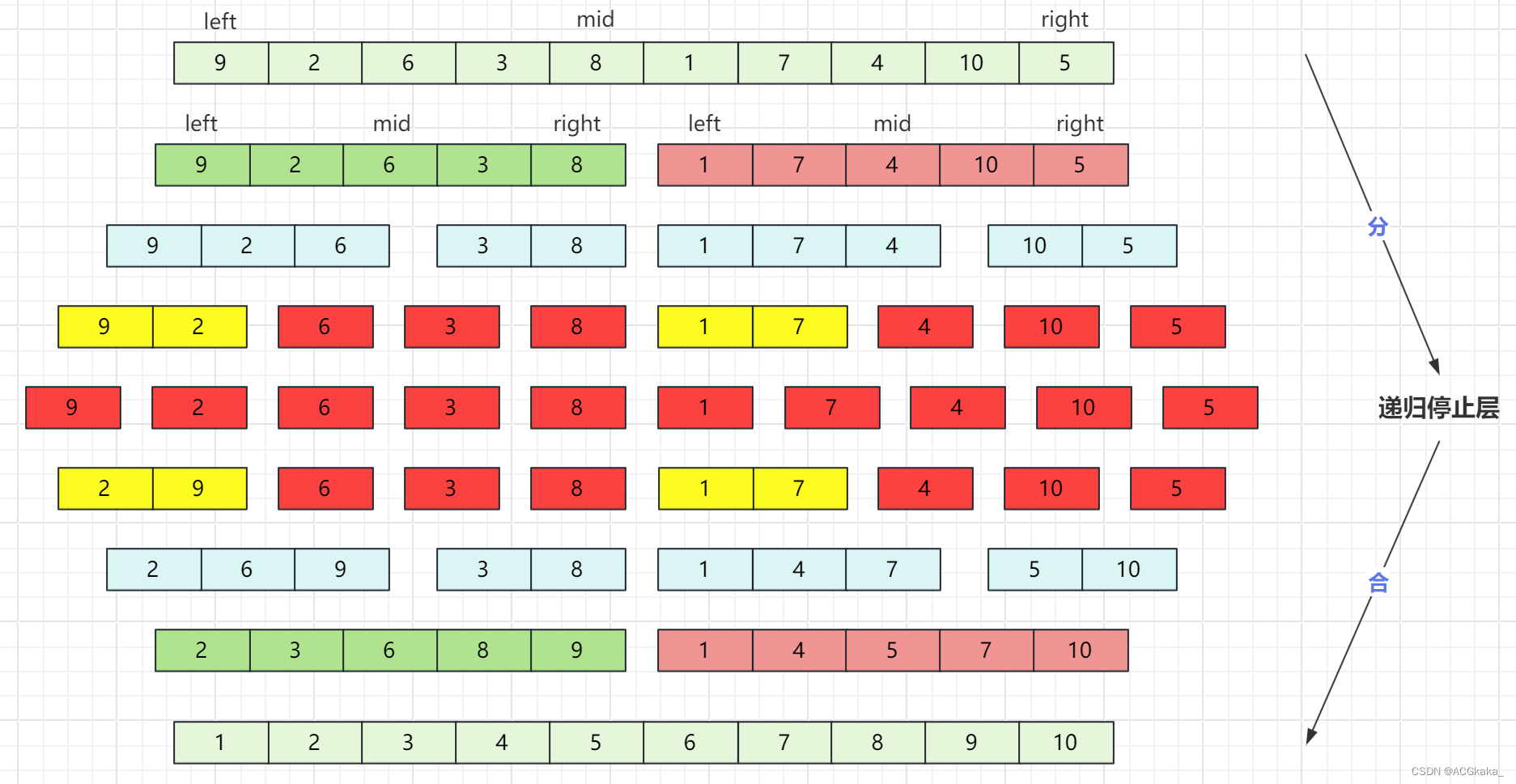
快速排序在划分的时候做了很多工作，而归并排序则恰恰相反。

思想：

先按照数量均匀划分为两块区域；
两块区域再各自进行划分，直到每块区域长度为1；
合并的时候再两两进行有序的合并。两个有序序列的合并仅需 O(n) 级别的时间复杂度即可完成。

而逆序数再归并排序基础上变形同样也是分治思想求解。

在这里插入图片描述

代码实现：

public int[] sortArray(int[] nums) {
    mergeSort(nums, 0, nums.length - 1);
    return nums;
}

/**
 * 归并排序
 * @param nums  数组
 * @param left  起始位置
 * @param right 结束位置
 */
private void mergeSort(int[] nums, int left, int right) {
    int mid = (left + right) / 2;
    if (left < right) {
        mergeSort(nums, left, mid);
        mergeSort(nums, mid + 1, right);
        merge(nums, left, mid, right);
    }
}

/**
 * 两两排序
 * @param nums  数组
 * @param left  起始位置
 * @param mid   中间位置
 * @param right 结束位置
 */
private void merge(int[] nums, int left, int mid, int right) {
    int[] arr = new int[right - left + 1];
    int l = left;
    int r = mid + 1;
    int index = 0;
    while (l <= mid && r <= right) {
        if (nums[l] <= nums[r]) {
            arr[index++] = nums[l++];
        } else {
            arr[index++] = nums[r++];
        }
    }
    while (l <= mid) {
        arr[index++] = nums[l++];
    }
    while (r <= right) {
        arr[index++] = nums[r++];
    }
    System.arraycopy(arr, 0, nums, left, arr.length);
}

2.4 最大子序列和

最大子数组和

题目：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

思路：

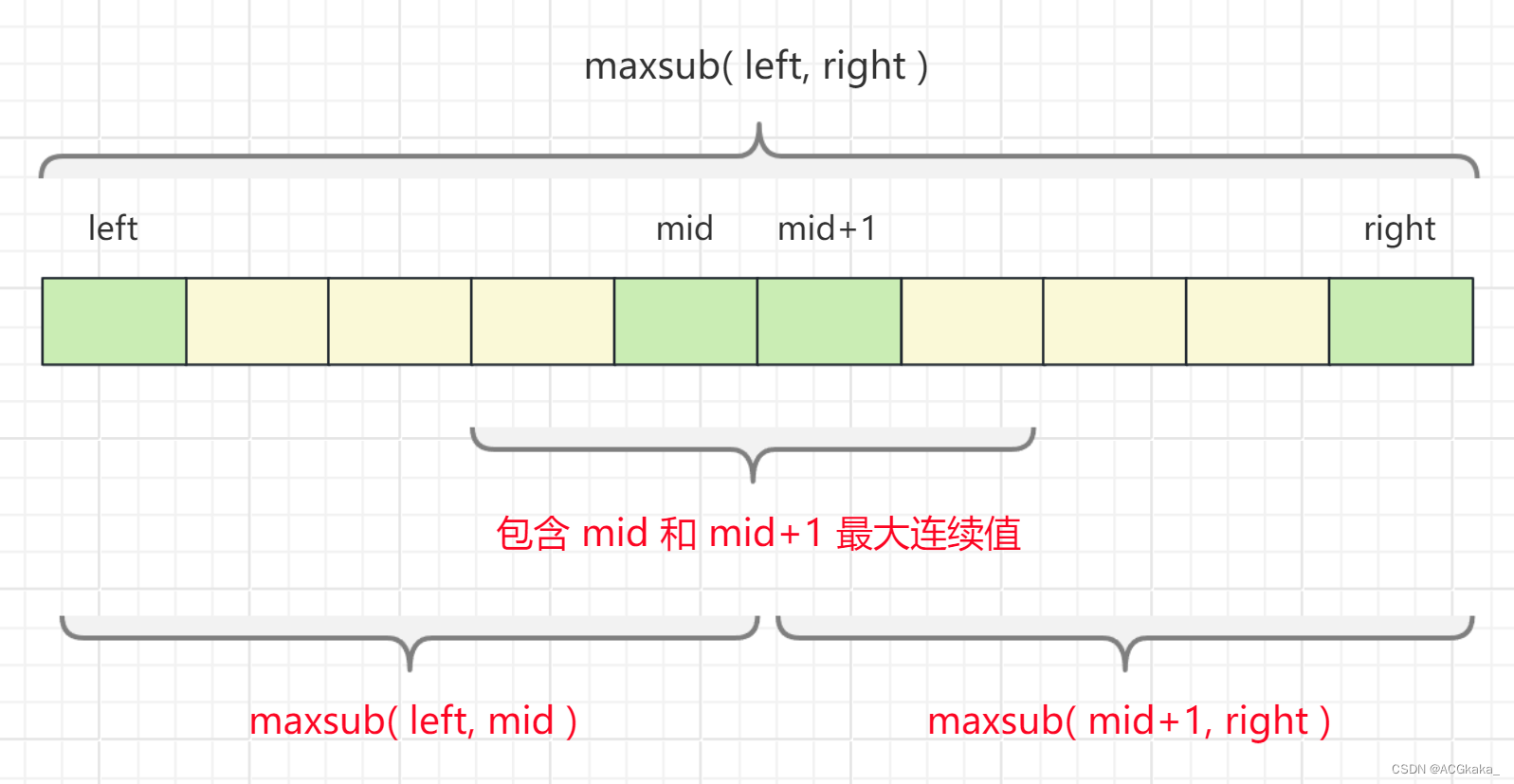
最大子序列和问题，我们可以使用 动态规划 的解法，也可以使用 分治算法 来解决问题。最大子序列和 在合并的时候并不是简单的合并，因为 子序列和 涉及到一个长度的问题，所以 正确结果不一定全在最左侧或最右侧，可能出现结果的区域为：

完全在中间的左侧
完全在中间的右侧
包含中间左右两个节点的一个序列

在这里插入图片描述

代码实现：

public int maxSubArray(int[] nums) {
    return maxSub(nums, 0, nums.length - 1);
}

private int maxSub(int[] nums, int left, int right) {
    if (left == right) {
        return nums[left];
    }
    int mid = (left + right) / 2;
    // 计算完全在mid左边的最大值
    int maxSubLeft = maxSub(nums, left, mid);
    // 计算完全在mid右边的最大值
    int maxSubRight = maxSub(nums, mid + 1, right);

    // 计算包含mid的最大值
    int tmpMaxLeft = nums[mid];
    int tmpLeftSum = 0;
    for (int i = mid; i >= left; i--) {
        tmpLeftSum += nums[i];
        tmpMaxLeft = Math.max(tmpMaxLeft, tmpLeftSum);
    }
    int tmpMaxRight = nums[mid + 1];
    int tmpRightSum = 0;
    for (int i = mid + 1; i <= right; i++) {
        tmpRightSum += nums[i];
        tmpMaxRight = Math.max(tmpMaxRight, tmpRightSum);
    }
    int maxSubCenter = tmpMaxLeft + tmpMaxRight;

    if (maxSubCenter >= maxSubLeft && maxSubCenter >= maxSubRight) {
        return maxSubCenter;
    } else {
        return Math.max(maxSubLeft, maxSubRight);
    }
}