矩阵处理—转圈打印矩阵
与其明天开始,不如现在行动!
文章目录
- 转圈打印矩阵
- 1 题目描述
- 2 解决思路
- 3 代码实现
- 💎总结
转圈打印矩阵
1 题目描述
一个n行m列矩阵,需要从外围开始转圈打印,直到所有数据都被打印,如图:
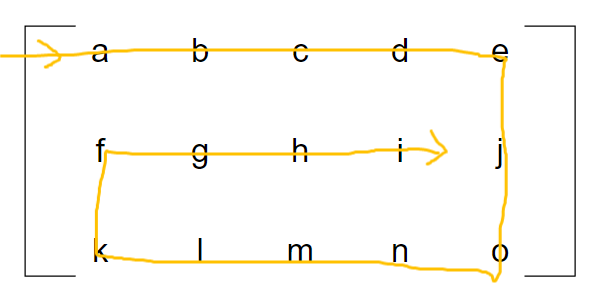
2 解决思路
最外围的打印终点的下一个就是里一层的打印起点
- 用四个指针,两个行指针,两个列指针,指针全都在要打印的那一层
- 行指针中,一个只在要打印的第一行移动,一个只在要打印的最后一行移动
- 列指针中,一个只在要打印的第一列移动,一个只在要打印的最后一列移动
3 代码实现
public class PrintMatrixSpiralOrder {
public static void spiralOrderPrint(int[][] matrix) {
int firstRow = 0;
int firstColumn = 0;
int endRow = matrix.length - 1;
int endColumn = matrix[0].length - 1;
while (firstRow <= endRow && firstColumn <= endColumn) {
printEdge(matrix, firstRow++, firstColumn++, endRow--, endColumn--);
}
}
private static void printEdge(int[][] matrix, int firstRow, int firstColumn, int endRow, int endColumn) {
if (firstRow == endRow) { // 如果矩阵是个列矩阵
while (firstColumn <= endColumn) {
System.out.print(matrix[firstRow][firstColumn++] + " ");
}
} else if (firstColumn == endColumn) { // 如果矩阵是个行矩阵
while (firstRow <= endRow) {
System.out.print(matrix[firstRow++][firstColumn] + " ");
}
}else { // 正常打印
int row = firstRow;
int column = firstColumn;
while (firstColumn != endColumn) {
System.out.print(matrix[firstRow][firstColumn++] + " ");
}
while (firstRow != endRow) {
System.out.print(matrix[firstRow++][firstColumn] + " ");
}
while (firstColumn != column) {
System.out.print(matrix[firstRow][firstColumn--] + " ");
}
while (firstRow != row) {
System.out.print(matrix[firstRow--][firstColumn] + " ");
}
}
}
public static void main(String[] args) {
int[][] matrix = new int[5][3];
int num = 1;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
matrix[i][j] = num++;
}
}
spiralOrderPrint(matrix);
}
}
💎总结
本文中若是有出现的错误请在评论区或者私信指出,我再进行改正优化,如果文章对你有所帮助,请给博主一个宝贵的三连,感谢大家😘!!!
