当前位置：首页 > article >正文

12.06 二叉树中等题2

article 2024/9/23 16:23:11

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

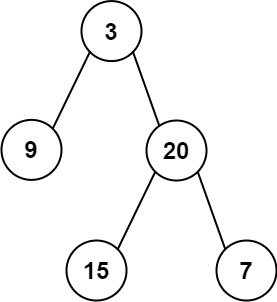
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

思路：后序遍历的数组中最后一个元素会是根节点，

有了根节点，可以在中序遍历数组中分出根节点的左子树和右子树，

即中序遍历数组中根节点左边的属于左子树，右边的属于右子树，即可分出左子树和右子树的中序遍历数组。

后序遍历数组中左子树和右子树的个数都要等于inorder数组的子树，即可分出左子树和右子树的后序遍历数组。

细节：根据思路可以用递归来做

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findIndex(vector<int>& nums,int target)
    {
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]==target) return i;
        }
        //没有这个值
        return -1;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size()==0) return nullptr;
        //查找根节点在中序遍历数组中的下标
        int rootVal=postorder[postorder.size()-1];
        auto rootIndex=findIndex(inorder,rootVal);
        //分别为
        //左子树的中序遍历数组 左子树的后续遍历数组
        // 右子树的中序遍历数组  右子树的后续遍历数组
        vector<int> leftInorder(inorder.begin(),inorder.begin()+rootIndex);
        // vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());
        vector<int> leftPostorder(postorder.begin(),postorder.begin()+rootIndex);
        vector<int> rightInorder(inorder.begin()+rootIndex+1,inorder.end());
        vector<int> rightPostorder(postorder.begin()+rootIndex,postorder.end()-1);


        TreeNode* root=new TreeNode(rootVal,
        buildTree(leftInorder,leftPostorder),
        buildTree(rightInorder,rightPostorder));

        
        return root;
    }
};

时间复杂度：O(n)，其中 n是树中的节点个数。.

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

思路：中序遍历二叉搜索树后的结果会是单调递增且无重复的。只需要对中序遍历的结果进行判定即可。

用双指针判断是否为单调递增的数组。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void midOrder(TreeNode* root,vector<int>& midResult)
    {
        if(!root) return;
        else
        {
            midOrder(root->left,midResult);
            midResult.push_back(root->val);
            midOrder(root->right,midResult);
        }
    }
    bool isValidBST(TreeNode* root) {
        //中序遍历的结果 得是单调递增且无重复的
        vector<int> midResult;
        midOrder(root,midResult);
        //判断是否是单调递增且无重复的
        if(midResult.size()<=1) return true;
        int left=0,right=1;
        while(right<midResult.size())
        {
            if(midResult[left]>=midResult[right]) return false;
            left++;
            right++;
        }
        return true;
    }
};