排序算法介绍(一)插入排序
0. 简介
插入排序(Insertion Sort) 是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用 in-place 排序(即只需用到 O(1) 的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
1. 插入排序的实现
插入排序的基本思想:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
插入排序过程演示:
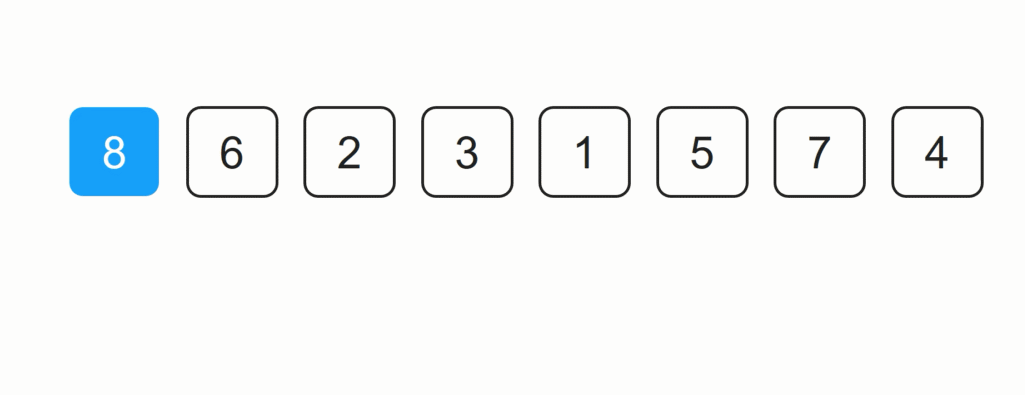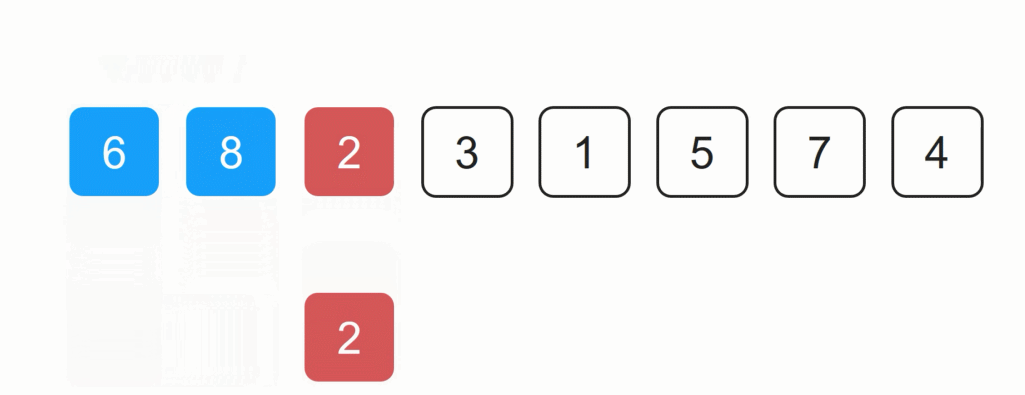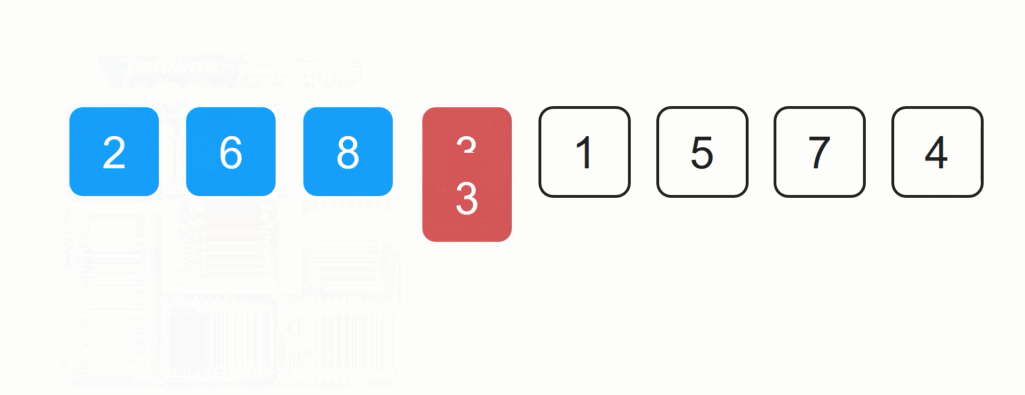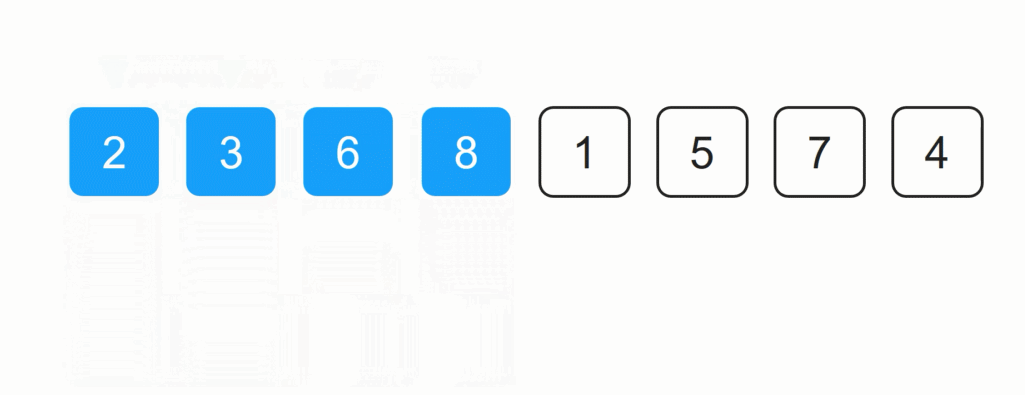
2. 插入排序时空间复杂度分析
插入排序的时间复杂度和空间复杂度如下:
-
时间复杂度:
- 最坏情况(逆序):每次插入都需要移动元素,总共需要移动的次数较多,所以时间复杂度是 O(n^2)。
- 最好情况(已排序):每次插入只需要比较一次,所以时间复杂度是 O(n)。
- 平均情况:时间复杂度是 O(n^2)。
-
空间复杂度:
- 插入排序只需要一个额外空间用于临时存储要插入的元素,所以空间复杂度是 O(1)。
总结:插入排序的平均和最坏情况时间复杂度都是 O(n^2),空间复杂度是 O(1)。
需要注意的是,插入排序适用于部分已排序的情况,这时其效率会相对较高。
3. 插入排序C语言代码
C代码实现:
#include <stdio.h>
void insertionSort(int arr[], int n) {
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
//将arr[0..i-1]中大于key的元素移动到当前位置之前的一个位置
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
void printArray(int arr[], int n) {
int i;
for (i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printArray(arr, n);
return 0;
}代码详解:
void insertionSort(int arr[], int n)函数定义了一个对整数数组arr[]进行插入排序的函数,其中n是数组的长度。- 在
for循环中,从数组的第二个元素开始(索引为1),每一个元素都被视为需要插入到已排序子数组的新元素。key存储了当前正在考虑的元素的值。 while循环用于移动所有大于key的已排序元素向右移动一位,以便为key提供空间。一旦找到key的正确位置或到达数组的开头,循环就会停止。然后,将key插入到正确的位置。printArray函数用于打印已排序的数组。在main函数中,我们定义了一个需要排序的数组,并调用insertionSort函数进行排序。最后,打印已排序的数组。
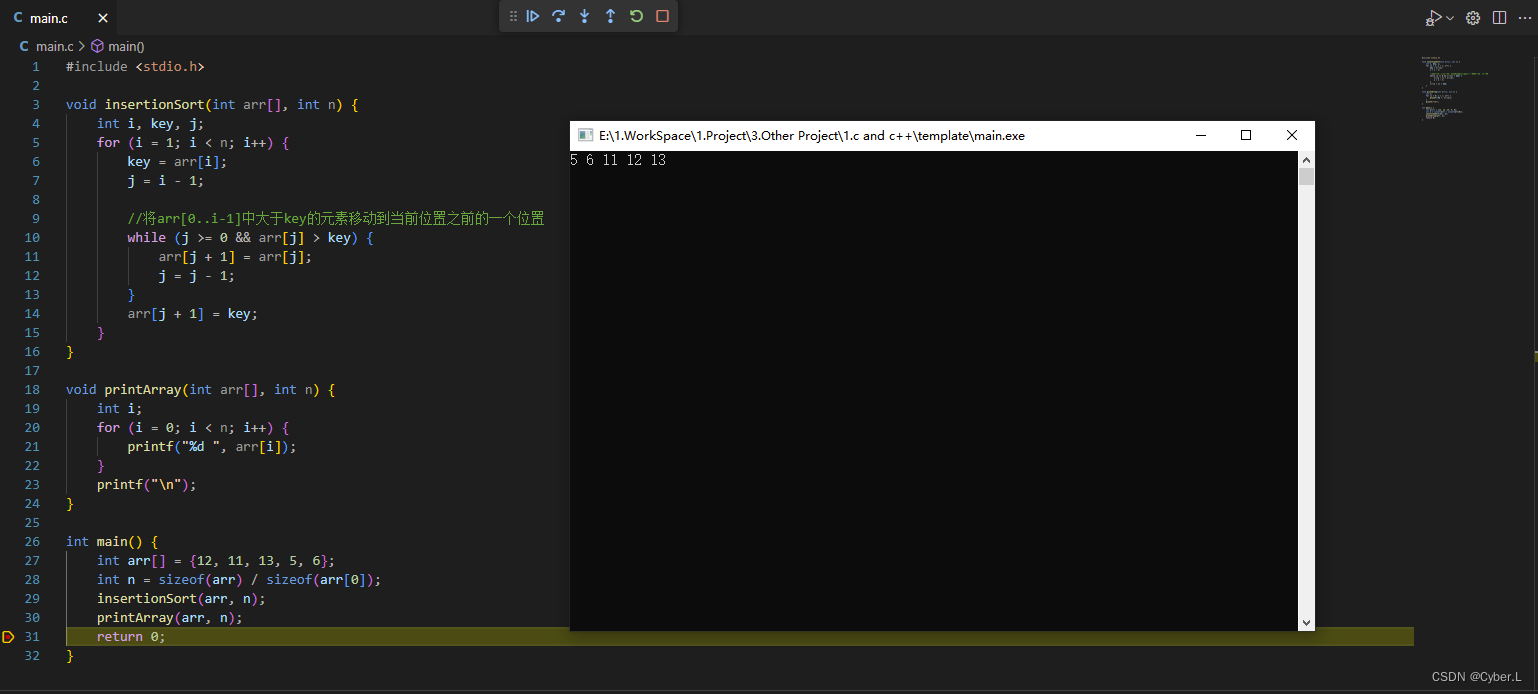
4. 插入排序代码运行结果
代码运行结果: